[NOI2008] 糖果雨

神题啊！干了一年才AC

首先由于各个操作的时间严格上升，因此在某此操作中，还没被删除的云朵是可以是为永久存在的；这样，又由于云的运动速度大小相同，即周期都为2len，将云的左端点一个周期的往返运动画在T(ime)-P(osition)图象上，类似下图中的蓝线；而红线即为云朵右端的图像。

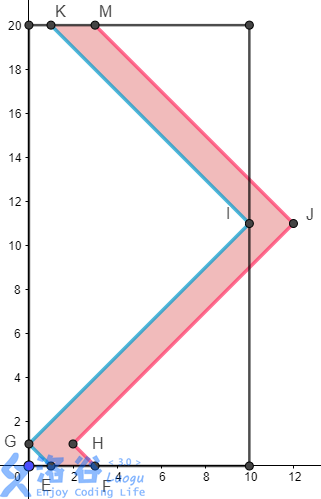
（图片来源@_rqy，侵删）

对于一个云朵Ci=(T,colour,L,R,d)，暴力模拟求出它的宽度、在0时刻（时间摸2len意义下）左端的位置及此时的运动方向，这样就能确定对应的左右折线，称他们为折线Bi、Ri。

对于询问Qi=(T,L,R)，可以看作求与线段(L,T)-(R,T)相交的不同云朵的折线数量。即sigma i [Bi或Ri与询问线段相交]的值，这可以更优美地表达为(sigma i [Ri包含点(R,T)或者在点(R,T)左边])-(sigma i [Bi在点(L,T)左边])。

所有时刻为正整数，涉及的所有点都为整点，可知式子的前后部分同质，即核心是求在包含某点或在某点左边的折线的数目。直接处理并不好做，可以考虑把坐标系旋转+平移，使得所有的折线段垂直或平行于坐标轴。例如

“在左边”变成了“在下边”，变得方便维护了，一个二维前缀和的形式。但我不清楚为什么有人单独维护R折线时，只用到了3*len的长宽，这应该是能被卡的。

#include <bits/stdc++.h>
#define pt pair<int,int>
#define mpt make_pair
using namespace std;

const int N=2e5+5;
const int LEN=1e3+5;

int n,len;
int L[N],R[N],D[N];
int bit[2][4*LEN][4*LEN];
int sum(int cur,pt p,int w=0) {
    auto bit=::bit[cur];
    for(int x=p.first; ; x-=x&-x) {
        for(int y=p.second; y>0; y-=y&-y) 
            w+=bit[x][y];
        w+=bit[x][0];
        if(!x) break;
    } 
    return w;
}
void add(int cur,pt p,int w) {
    auto bit=::bit[cur];
    for(int x=p.first; x<=4*len; x+=x&-x) {
        for(int y=p.second; y<=4*len; y+=y&-y) {
            bit[x][y]+=w; if(!y) break;
        } if(!x) break;
    }
}
#define DIRECT if(l==0) d=1; if(l==len) d=-1;
pt rotate(int x,int y) {return mpt(x-y+2*len,x+y);}

int main() {
    scanf("%d%d",&n,&len);
    for(int opt,T,c,l,r,d,s; n--; ) {
        scanf("%d%d",&opt,&T); T%=2*len;
        if(opt==1) {
            scanf("%d%d%d%d",&c,&l,&r,&d); r-=l;
            DIRECT;
            for(; T; T%=2*len) {
                s=min(d>0?len-l:l,2*len-T);
                l+=d*s; T+=s; DIRECT;
            }
            L[c]=l,R[c]=r,D[c]=d;
            for(s=0; T<2*len-1;) {
                l+=d*s; T+=s; DIRECT;
                if(T==0&&d==1) {
                    add(0,rotate(l,T),1);
                    add(1,rotate(l+r,T),1);
                } else if(T==2*len-1&&((l<len&&d<0)||!l)) {
                    add(0,rotate(l,T),1);
                    add(1,rotate(l+r,T),1);
                } else if(0<T&&T<2*len-1) {
                    add(0,rotate(l,T),d);
                    add(1,rotate(l+r,T),d);
                }
                s=min(d>0?len-l:l,2*len-1-T);
            }
        } else if(opt==2) {
            scanf("%d%d",&l,&r); 
            if(l==0) printf("%d\n",sum(0,rotate(r,T)));
            else printf("%d\n",sum(0,rotate(r,T))-sum(1,rotate(l-1,T)));
        } else if(opt==3) {
            scanf("%d",&c); 
            l=L[c],r=R[c],d=D[c]; 
            for(T=s=0; T<2*len-1;) {
                l+=d*s; T+=s; DIRECT;
                if(T==0&&d==1) {
                    add(0,rotate(l,T),-1);
                    add(1,rotate(l+r,T),-1);
                } else if(T==2*len-1&&((l<len&&d<0)||!l)) {
                    add(0,rotate(l,T),-1);
                    add(1,rotate(l+r,T),-1);
                } else if(0<T&&T<2*len-1) {
                    add(0,rotate(l,T),-d);
                    add(1,rotate(l+r,T),-d);
                }
                s=min(d>0?len-l:l,2*len-1-T);
            }
        }
    }
    return 0;
}