[NOI2006] 网络收费

贼有意思的一道题。考虑把费用给转化一下，观察

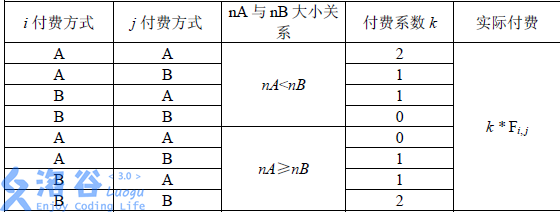
如果定义叶节点的状态 {{A,0},{B,1}}，非叶节点的状态 {{nA>=nB,0},{nA<nB,1}}，结合上图可以得出

• 叶节点x,y(x<y)的状态相同
  • 叶节点状态与lca(x,y)状态相同，费用0
  • 叶节点状态与lca(x,y)状态不同，费用2f[x,y]
• 叶节点x,y(x<y)的状态不同，费用f[x,y]

技巧化的，直接定义叶节点x关于祖先d的权值为h(x,d)=[x的状态≠d的状态]Σf[x,y]，其中y是d子树管辖的不等于x的叶节点。

这样一来，如果实现清楚了祖先的状态，x的贡献就等于Σh(x,d)了。

于是考虑枚举祖先的状态并进行dp，设f[x,i]表示在x子树中出现了i个0状态叶节点的最小代价，转移部分比较简单，参考代码就行。

没讲太清楚明天补补吧。千万记得初始化dp数组！！！

update：已经很详尽了还有什么要不补的啊喂，滚去睡觉了233

#include <bits/stdc++.h>
#define ls (x<<1)
#define rs (x<<1|1)
using namespace std;
const int inf=0x3f3f3f3f;

int n;
int cv[2050],ori[2050],tmp[2050];
int dp[2050][2050],v[2050][2050];
int lq[12],rq[12];

void dfs(int x,int l,int r,int set,int dep) {
    memset(dp[x],inf,sizeof dp[x]);
    if(l==r) {
        dep--;
        dp[x][0]=ori[l]?0:cv[l];
        dp[x][1]=ori[l]?cv[l]:0;
        for(int i=1; i<=dep; ++i) {
            int mid=(lq[i]+rq[i])>>1;
            int key=!(1&(set>>(dep-i))); //相异有贡献
            if(l<=mid) dp[x][key]+=v[l][rq[i]]-v[l][mid];
            else dp[x][key]+=v[l][mid]-v[l][lq[i]-1];
        }
        return;
    }
    int mid=(l+r)>>1,len=r-l+1;
    lq[dep]=l,rq[dep]=r;

    dfs(ls,l,mid,set<<1,dep+1);
    dfs(rs,mid+1,r,set<<1,dep+1);

    for(int i=0; i<len/2; ++i)
    for(int j=0; j<=i; ++j) 
        dp[x][i]=min(dp[x][i],dp[ls][j]+dp[rs][i-j]);

    dfs(ls,l,mid,set<<1|1,dep+1);
    dfs(rs,mid+1,r,set<<1|1,dep+1);
    for(int i=len/2; i<=len; ++i)
    for(int j=0; j<=i; ++j) 
        dp[x][i]=min(dp[x][i],dp[ls][j]+dp[rs][i-j]);
}

int main() {
    scanf("%d",&n); n=1<<n;
    for(int i=1; i<=n; ++i) scanf("%d",ori+i);
    for(int i=1; i<=n; ++i) scanf("%d",cv+i);
    for(int i=1; i<=n; ++i) 
    for(int j=i+1; j<=n; ++j) {
        scanf("%d",&v[i][j]);
        v[j][i]=v[i][j];
    }
    for(int i=1; i<=n; ++i) 
    for(int j=1; j<=n; ++j) 
        v[i][j]+=v[i][j-1];
    dfs(1,1,n,0,1);
    int ans=inf;
    for(int i=0; i<=n; ++i) 
        ans=min(ans,dp[1][i]);
    printf("%d\n",ans);
    return 0;
}