[IOI2007] sails 船帆
显然答案与杆的顺序无关(按每个高度考虑)。
从高到低考虑杆,设此时的状态为\(S\),\(S[i]\)是高度\(i\)的帆的数目,初始全为\(0\),当前杆的高度为\(h\),杆上需要放置的帆的数目为\(k\),贪心地,假设两个高度的同等宜选,优先选择更高的;帆尽量放置在\(S[i]=0(i\le h)\)的高度上,若还有剩余,设剩下\(t(t\le k)\)个,则放置在除去以选择的高度以外,\(S[i](i\le h)\)前\(t\)小的位置。
整理一下,每次选出\(S[1\cdots h]\)中前\(k\)小的(相同大小选下标较大的)高度放置帆。
{5,3} 0 0 1 1 1 +0
{4,3} 1 1 2 1 1 +1
{4,1} 1 2 2 1 1 +1
{3,2} 2 2 3 1 1 +3
{3,2} 3 3 3 1 1 +4
{2,1} 3 4 3 1 1 +3
但是此时\(S\)似乎不好维护。。考虑将过程倒过来,从低到高考虑杆,(\(S\)一开始为空集,其余定义相同),假设两个高度同等宜选,优先选择更低的,其余大致相同。即每次选出\(S[1\cdots h]\)中前\(k\)小的(相同大小选下标较小的)高度放置帆。
{2,1} 1 0 +0
{3,2} 1 1 1 +0
{3,2} 2 2 1 +2
{4,1} 2 2 1 1 +0
{4,3} 3 2 2 2 +4
{5,3} 3 3 3 2 1 +4
这样用平衡树维护\(S\)(初始大小为0,每次长度变化时补0节点),每次查询全局前\(k\)小然后整体加一即可。(省去了下标范围的约束)。进一步可发现,连下标都不用维护了
巧妙的分割线(之前的splay已经弃坑了)
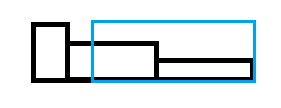
观察各个时态的\(S\),发现它总是一个单调不增的序列,把某时态的\(S\)中相同且相邻分成一块,如图,蓝色方框表示将选出前\(k\)小的位置,注意被完全覆盖的块的高度可以直接区间+1,而割开的块区间+1的范围是反过来的,显然这样的块最多一块,于是可以上线段树来维护。
答案也不用每步累加,设\(S[i]\)表示最终状态上高度为\(i\)的帆的数目,显然总答案是\(\sum_i\frac{S[i](S[i]-1)}2\),这与因为从本文第一句照应。
#include <bits/stdc++.h>
#define LL long long
const int N=1e5+10;
namespace sgt {
struct sgtNode {
int mx,mn,add;
} t[N<<2];
#define ls (x<<1)
#define rs (x<<1|1)
void update(int x) {
t[x].mx=std::max(t[ls].mx,t[rs].mx);
t[x].mn=std::min(t[ls].mn,t[rs].mn);
}
void pushr(int x,int add) {t[x].mn+=add,t[x].mx+=add,t[x].add+=add;}
void pushdown(int x) {
if(t[x].add) pushr(ls,t[x].add),pushr(rs,t[x].add),t[x].add=0;
}
LL calc(int x,int l,int r) {
if(l==r) return 1LL*t[x].mx*(t[x].mx-1)/2;
int mid=(l+r)>>1; pushdown(x);
return calc(ls,l,mid)+calc(rs,mid+1,r);
}
void build(int x,int l,int r) {
t[x].mn=+1e9,t[x].mx=-1e9;
if(l==r) return; int mid=(l+r)>>1;
build(ls,l,mid); build(rs,mid+1,r);
}
void insert(int x,int l,int r,int p) {
if(l==r) return void(t[x].mx=t[x].mn=0);
int mid=(l+r)>>1; pushdown(x);
if(p<=mid) insert(ls,l,mid,p);
else insert(rs,mid+1,r,p);
update(x);
}
void modify(int x,int l,int r,int L,int R) {
if(L>R) return;
if(L<=l&&r<=R) return pushr(x,1);
int mid=(l+r)>>1; pushdown(x);
if(L<=mid) modify(ls,l,mid,L,R);
if(mid<R) modify(rs,mid+1,r,L,R);
update(x);
}
int getVal(int x,int l,int r,int p) {
if(t[x].mn==t[x].mx) return t[x].mn;
int mid=(l+r)>>1; pushdown(x);
if(p<=mid) return getVal(ls,l,mid,p);
else return getVal(rs,mid+1,r,p);
}
int getRangeL(int x,int l,int r,int w) {
if(l==r) return l;
int mid=(l+r)>>1; pushdown(x);
if(t[ls].mn<=w) return getRangeL(ls,l,mid,w);
else return getRangeL(rs,mid+1,r,w);
}
int getRangeR(int x,int l,int r,int w) {
if(l==r) return l;
int mid=(l+r)>>1; pushdown(x);
if(t[rs].mx>=w) return getRangeR(rs,mid+1,r,w);
else return getRangeR(ls,l,mid,w);
}
}
int n,m;
std::pair<int,int> a[N];
int main() {
scanf("%d",&n);
for(int i=1; i<=n; ++i) {
scanf("%d%d",&a[i].first,&a[i].second);
m=std::max(m,a[i].first);
}
std::sort(a+1,a+n+1);
sgt::build(1,1,m);
for(int i=1,R=0; i<=n; ++i) {
while(R<a[i].first) sgt::insert(1,1,m,++R);
int pos=R-a[i].second+1; //被割开的位置
int val=sgt::getVal(1,1,m,pos);
int rgl=sgt::getRangeL(1,1,m,val);
int rgr=sgt::getRangeR(1,1,m,val);
// std::cout<<val<<' '<<rgl<<' '<<rgr<<std::endl;
sgt::modify(1,1,m,rgr+1,R);
sgt::modify(1,1,m,rgl,rgl+a[i].second-(R-rgr)-1);
}
printf("%lld\n",sgt::calc(1,1,m));
return 0;
}

