定点补码乘法器小记
参考链接:
本小记几乎是对《计算机体系结构基础 第三版》定点补码乘法器的个人描述,补充地方在于最后华莱士树的部分
硬件模拟软件
软件方式即类似我们手工计算,如计算1101 * 0101
+00001101(乘数最低位1,结果加上被乘数。将乘数右移,被乘数左移)
+00000000(乘数最低位0,结果加0,移位,下同)
+00110100
+00000000
=01000001

这个乘法器有两个明显的特点:
- 对于N位乘法需要N拍
- 只能用于计算无符号数乘法,如果要计算补码乘法则必须将两者转为绝对值,运算结束后再根据原始的符号决定正负,转换为对应的相反数或本身。
就第2点来看,补码加法只需要无脑加就能得出结果,然而补码乘法竟然还得根据符号做出这样的转换,显得有点麻烦并且有点不对等了。因此下面引出的解决方案,让补码乘法也能像补码加法那样,“无脑乘”,省去最后做出的转换步骤。
无脑乘
根据补码的定义,可以将乘数转换为如下形式:
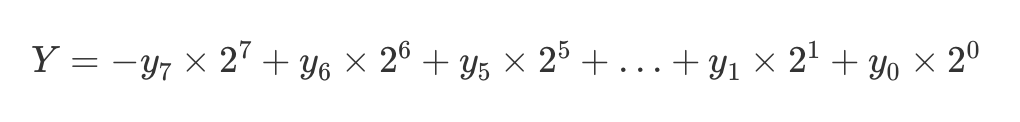
乘法即可表示为
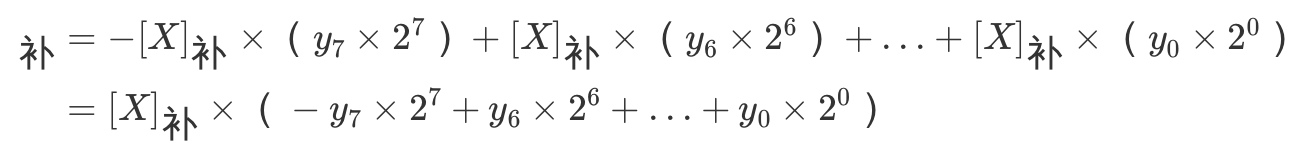
可以看到除了第N个部分积\(-[X]_补\times(y_7\times2^7)\)需要加上负号外,其余部分积可套用之前的电路来计算。因此在原来无符号乘法电路的基础上,我们只需要对最后一个部分积进行特判,就能实现补码乘法了,即最终出来的结果不用根据符号再作转换。

所谓前人种树后人乘凉,有了下面的Booth乘法器,这个无脑乘电路又略显逊色了,逊色在于这个特判需要额外的状态机来控制,增加了硬件复杂度,相比之下Booth算法对机器更加友好(统一操作,省去特判)。
Booth乘法器
对电路的改造依然是基于对表达式的转换:下图对乘数Y的表示做的一番转换,使其每一个加法项变成统一的形式:\((y_{i-1}-y_{i})\times2^i\),其中\(y_{-1}=0\)
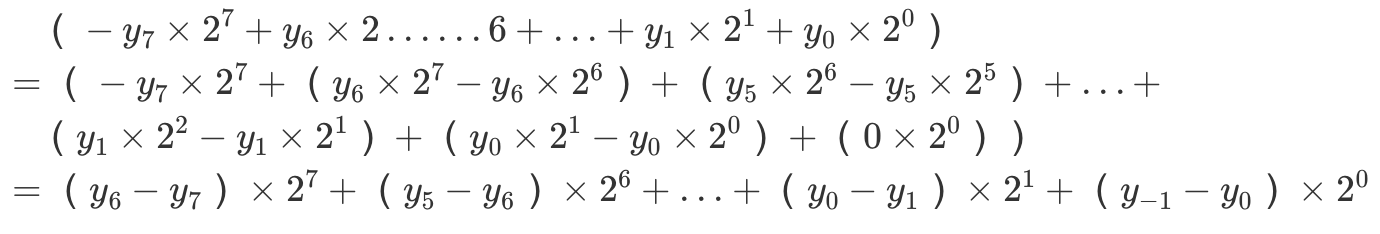
诶,这样一来,对于第\(i\)个部分积就等于\([X]_补\times(y_{i-1}-y_i)\times2^i\),也就是我们每次只需要通过乘数的最后两位确定如何将被乘数加到结果当中:
| yi | yi-1 | 操作 |
|---|---|---|
| 0 | 0 | 不需要加(+0) |
| 0 | 1 | 补码加X(+[X]补) |
| 1 | 0 | 补码减X(-[X]补) |
| 1 | 1 | 不需要加(+0) |
这样我们就统一了部分积的计算规则,省去了特判状态机。然鹅此时N位乘法还是需要N拍,因此可以将式子继续变换:
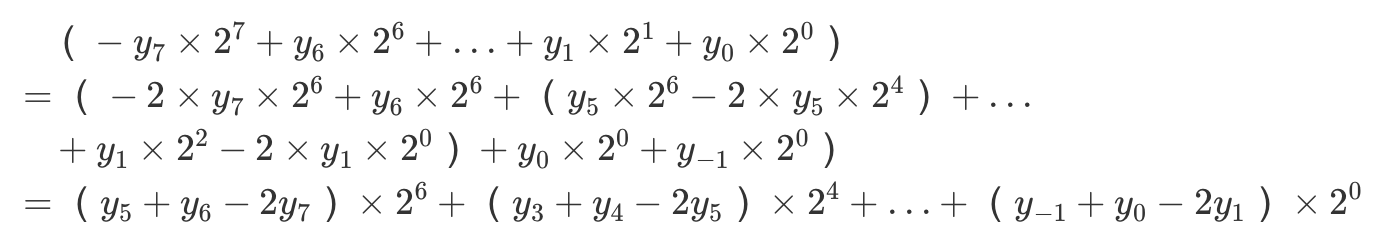
这个式子的结果也是一目了然了:从之前的每次移位1位,变成移位2位,并且部分积从之前的根据乘数后2位来确定变成根据乘数后3位来确定:
| yi+1 | yi | yi-1 | 操作 |
|---|---|---|---|
| 0 | 0 | 0 | 不需要加(+0) |
| 0 | 0 | 1 | 补码加X(+[X]补) |
| 0 | 1 | 0 | 补码加X(+[X]补) |
| 0 | 1 | 1 | 补码加2X(+[X]补左移) |
| 1 | 0 | 0 | 补码减2X(-[X]补左移) |
| 1 | 0 | 1 | 补码减X(-[X]补) |
| 1 | 1 | 0 | 补码减X(-[X]补) |
| 1 | 1 | 1 | 不需要加(+0) |
这样N位乘法只需要N/2-1次加法,使用N/2拍完成。类似地可以将式子变换成移位3位、4位等,不过这样需要的硬件就更加复杂,两位乘算法更适合硬件实现,更为实用(应该是吧qwq)。
下面介绍Booth两位乘的具体实现细节:假设[X]补的二进制格式写作x7x6x5x4x3x2x1x0,再假设部分积P等于p7p6p5p4p3p2p1p0+c,那么根据上表有:

为了得到\(p_i\)的逻辑表达式,为了便于信号复用这里加入了中间信号\(S\),例如S+x信号在部分积选择为+X时为1,因此有:
\(pi=∼(∼(S_{−X}\&∼x_i)\&∼(S_{−2X}\&∼x_{i−1})\&∼(S_{+X}\&x_i) \& ∼(S_{+2X} \& x_{i−1}))\)
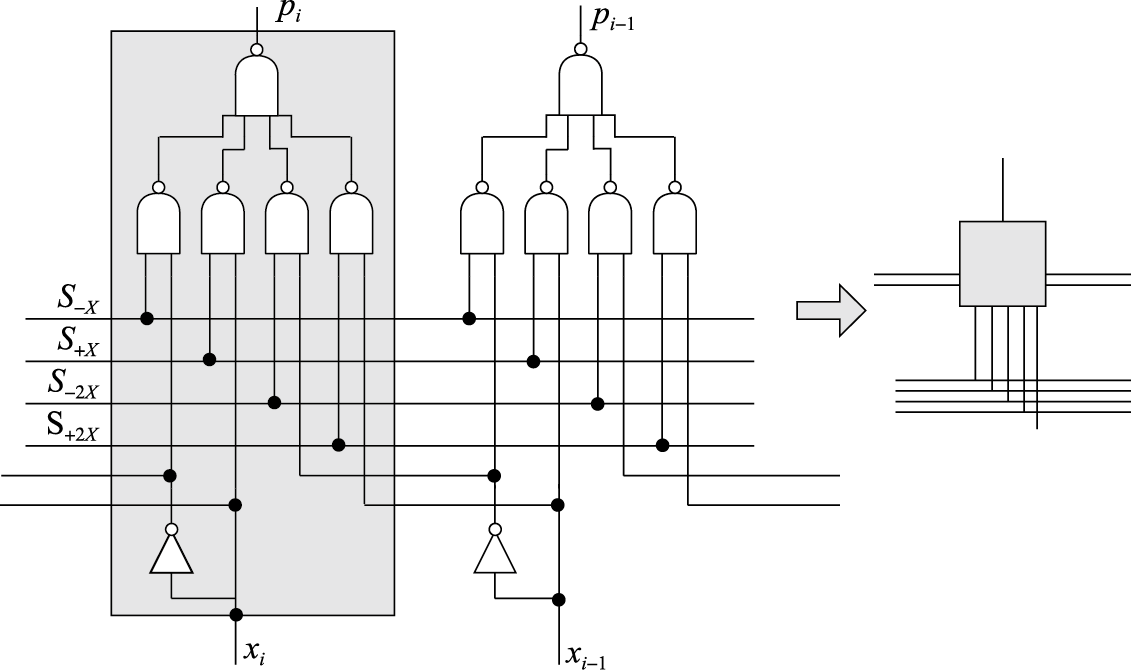
中间信号S又通过乘数Y后三位表示得到,如:\(S_{−x}=∼(∼(y_{i+1}\&y_i\&∼y_{i−1})\&∼{}(y_{i+1} \& ∼y_i \& y_{i−1}))\)

将上面两个部件连线得到Booth编码器(《胡伟武的计算机系统结构基础 第三版》中是这样命名这个部件的),其中输出信号\(c=S_{-X}|S_{-2X}\)
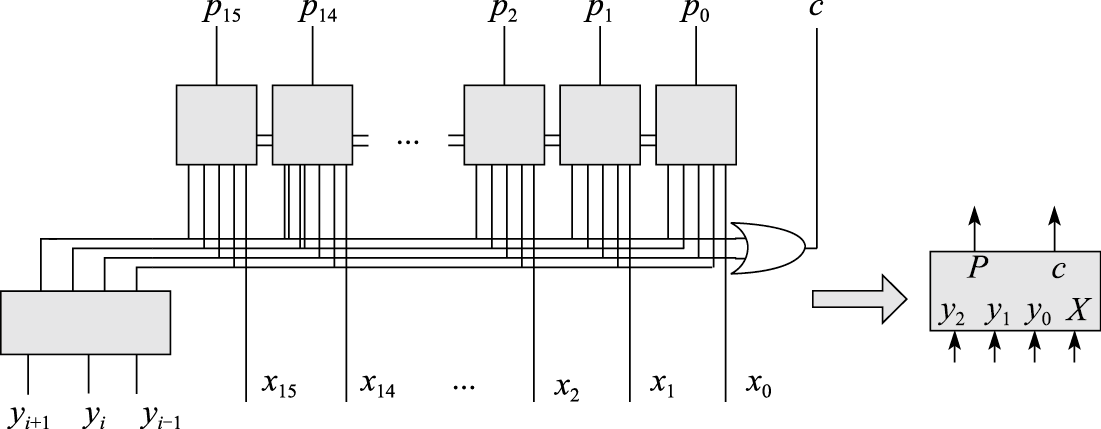
最后通过连接乘数、被乘数、加法器等部件构成两位Booth乘法器

其中被乘数、结果、加法器与部分积生成器的宽度都为2N位。
华莱士树
对于现代处理器来说,完成64位乘法需要32周期依然太慢,并且不支持流水操作。如果将上面每拍处理一次部分积的算法改造成,使用32个Booth编码器同时生成所有部分积,并用类二叉树的方式将部分积相加,第一拍执行16个加法、第二拍8个加法....通过这样大规模增加硬件的方法确实可以轻松流水,延迟也控制在一定的范围内,但是硬件开销实在太大。
华莱士树算法可以大幅降低多个数相加的硬件开销和延迟。
华莱士树算法在于全加器(FA)的巧妙利用,并且在该算法中FA有个更加合适的名称:保留进位加法器(CSA),CSA其实就是FA,只不过cin与两个加数的地位同等,看成三个数的加和。书中用FA这个名称讲解,而本小记认为在华莱士树中称之为CSA更合适。
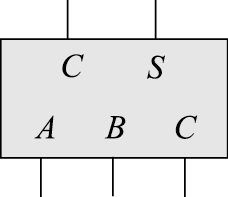
根据定义有A+B+C=S+(C<<1),注意等号前面的C是低位进位,后面的C是本位向高位的进位,不是同一个C。核心之处就在于将三个数A,B,C的加法转换了两个数S,C的加法。因此一个CSA实现了三个一位数的加法,注意这里所谓的“加法”得到的不是最终结果,而是得到两个N位的加数,也就是说经过华莱士算法之后,还需要一个正经的加法器(RCA、CLA等)将这两个数加起来。若没有其他说明,下面说的“加法”解释同上。
3个4位数的加法,则可用使用四个CSA实现:
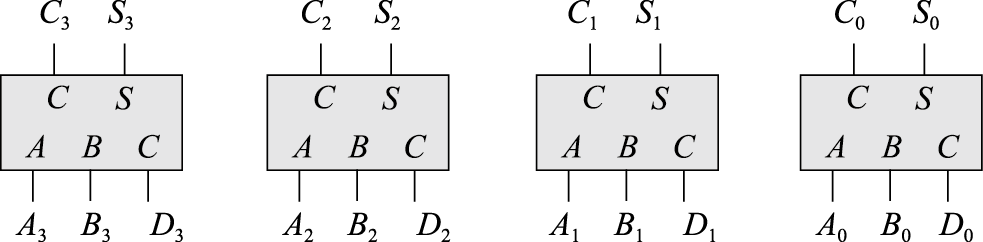
即:
\(\{A_3A_2A_1A_0\}+\{B_3B_2B_1B_0\}+\{D_3D_2D_1D_0\}=\{S_3S_2S_1S_0\}+\{C_2C_1C_00\}\)
仅考虑保留位宽4,因此\(C_3\)直接丢弃。
4个4位数加法实现:
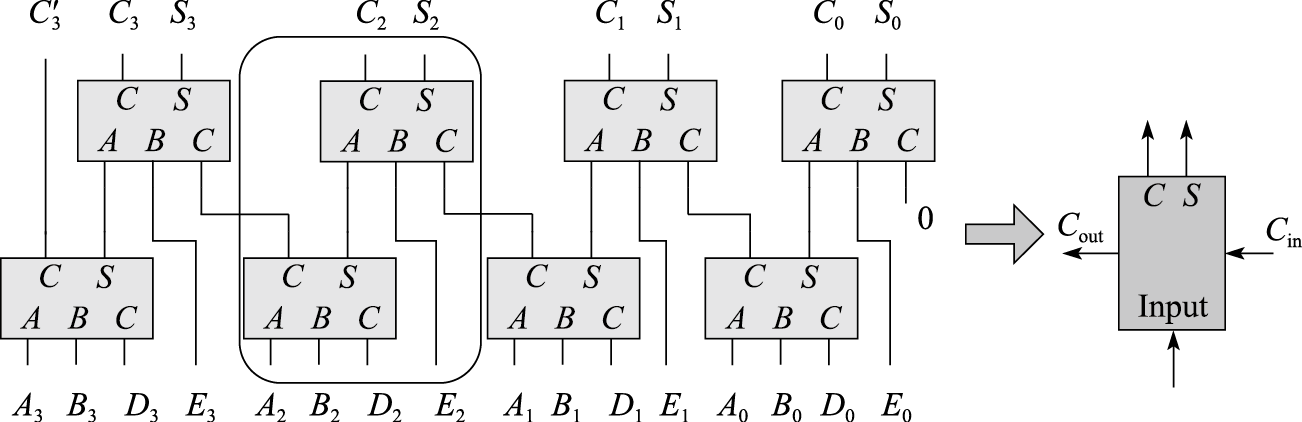
同样地,如果仅保留4位,则直接丢弃\(C_3\)和\(C3'\)。其中图中圈起来的部分即构成了一个4数相加的1位华莱士树,因此上图可以看为将4个4个1位数的华莱士树相连。
回到最初的问题,通过设置N/2个Booth编码器我们可以同时得到N/2个2N位的部分积,下一步通过设置2N个N/2数相加的1位华莱士树对这些部分积进行相加。例如N=16,经过Booth算法后输出8个宽度为32的部分积,即需要设置32个8数相加的1位华莱士树。类似4数相加的1位华莱士树,给出8数相加的1位华莱士树结构:
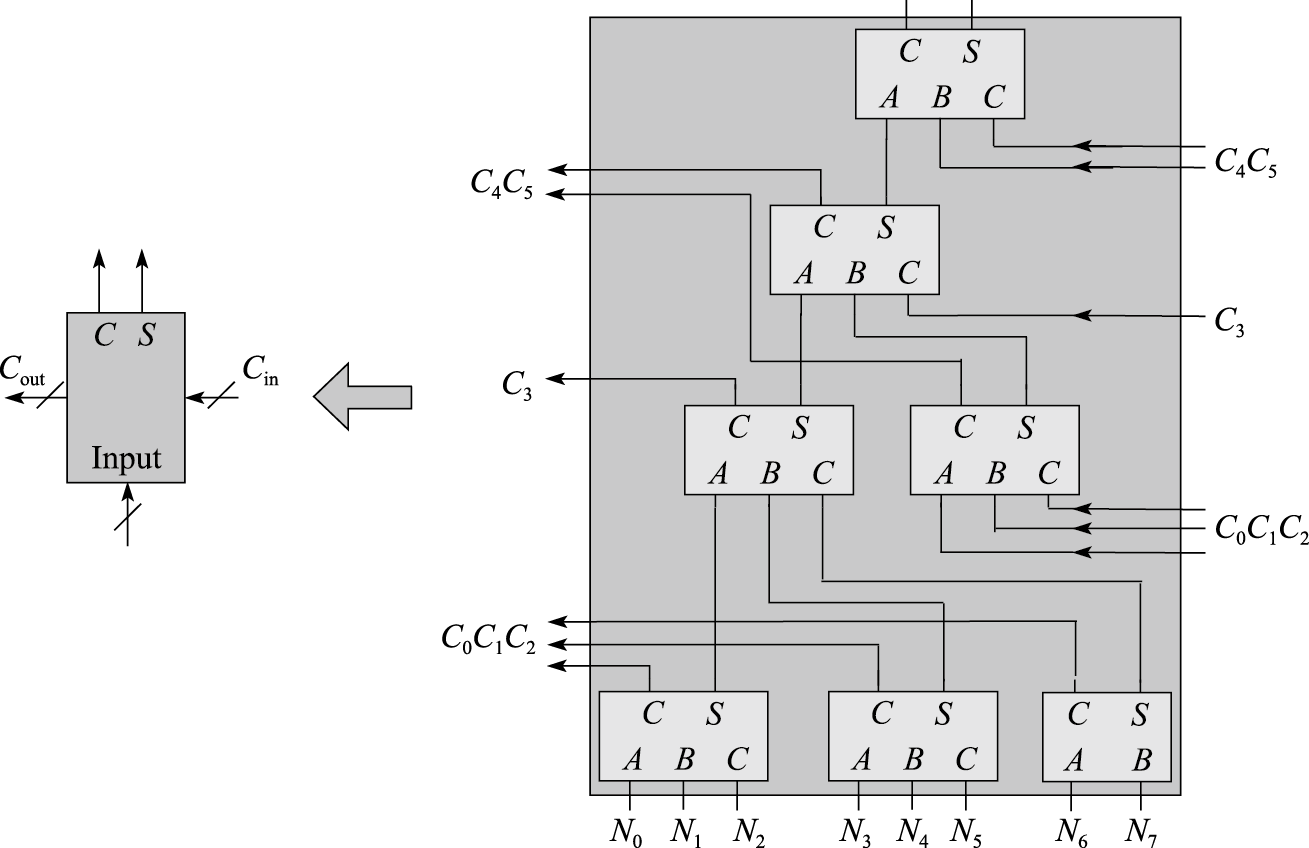
上图来自《计算及体系结构基础 第三版》,我一开始是疑惑为什么要这样构建这个华莱士树的,并且看了下面书中所谓“错误的华莱士树结构”之后,更加迷惑:
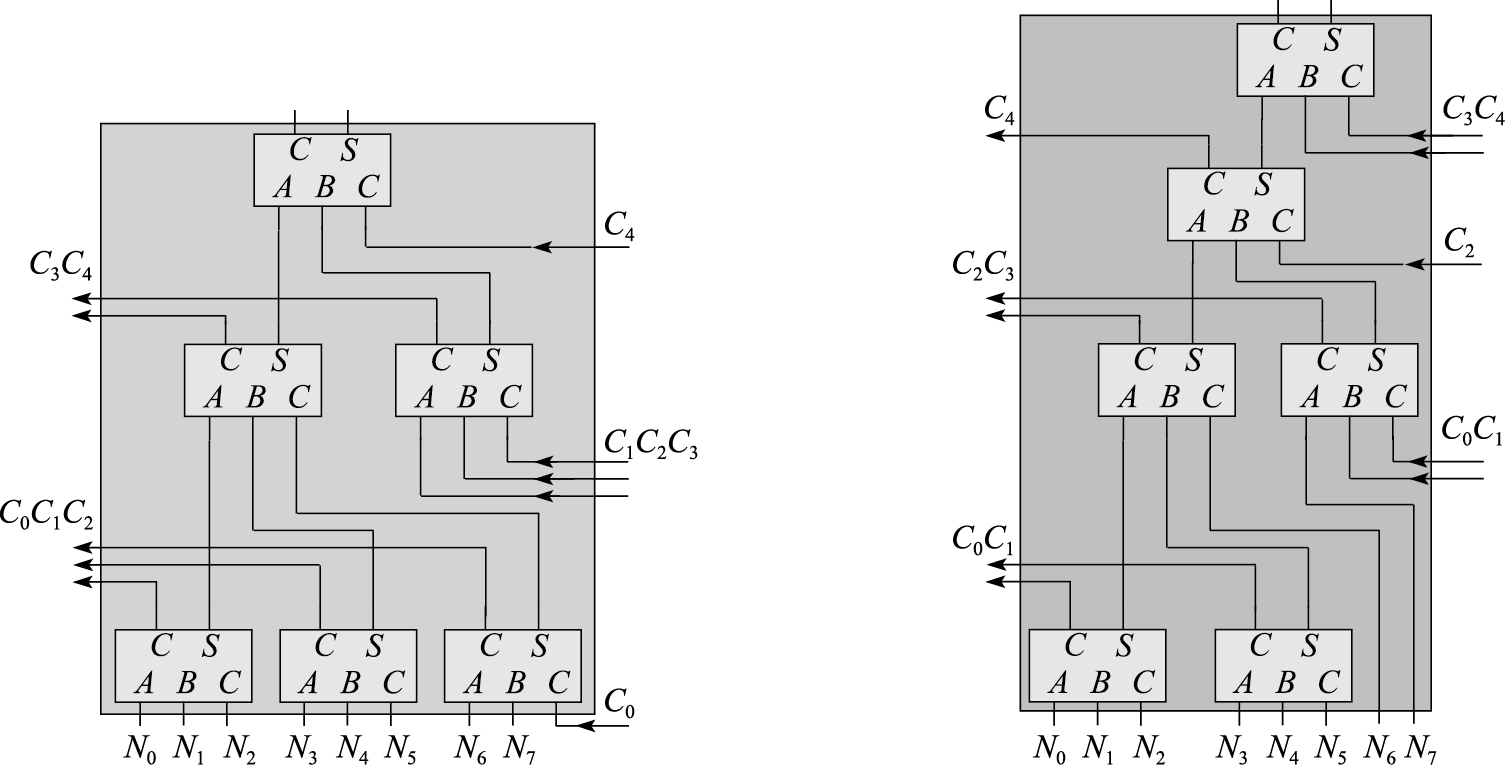
明明这两个结构也能出正确的结果,不同之处只是相比正确的华莱士树进位位少了一位。而书上指出这两个结构错的地方甚至都不一样。哎,只能先忽略所谓的错误,接着往下看。
到这里,我们已经拥有了Booth编码器与华莱士树结构,可以连线构造这个16位乘法器了!首先乘法器分为三层:
- 第一层是8个Booth编码器,分别输出8个部分积\(P_{0~7}\)与对应的\(c_{0~7}\)(不知道的建议回头重看Booth乘法器部分)
- 第二层是32个8数相加的1位华莱士树,相当于第\(i\)个华莱士树处理部分积的\(i\)位,部分积是32位,因此对应32个华莱士树,共8个部分积因此需要8数相加的1位华莱士树。根据华莱士树的定义,这层输出两个32位的加数S和(C<<1)
- 第三层将上层的两个加数用加法器进行相加得出结果
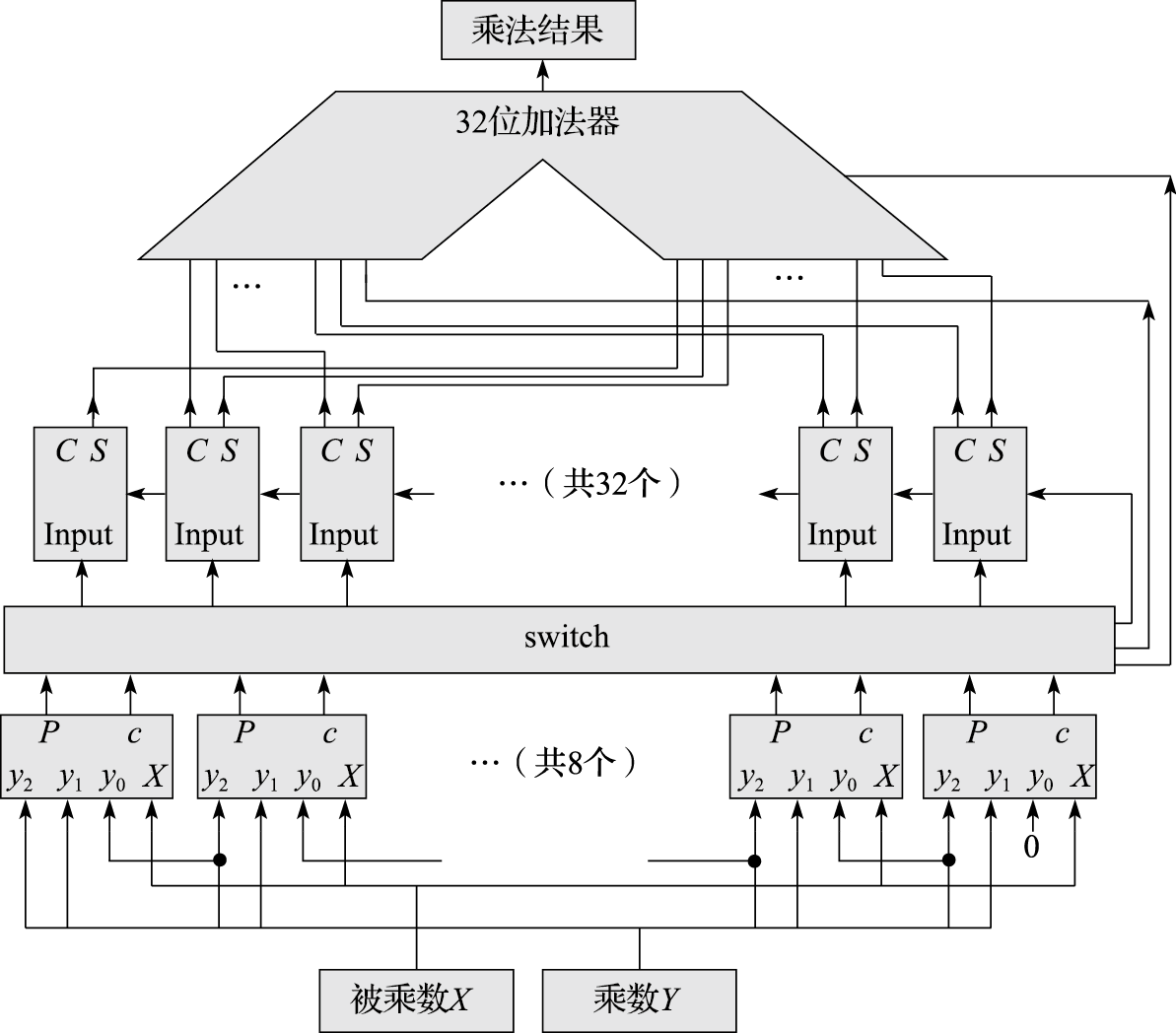
在第一层和第二层之间的switch用于收集8个Booth核心生成的8个32位数,进行类似矩阵转置的操作,重新组织为32组、8个一位数相加的格式作为华莱士树的输入,起到适配器的作用。至此我们得到了一个Booth x 华莱士树算法定点补码乘法器
另外,8个Booth编码器输出的8个c从switch的右边原封不动输出,其中6个c从最右边的华莱士树作为进位输入,1个c输入32位加法器,剩下一个则替换{C30,C29...,C0,0}中的最低位0,即加法器左边的输入为{C30,C29...,C0,c}。诶,到这里我们发现,如果使用的是上面两个“错误的华莱士树”,那么只有5个进位输出,对于这个乘法器的整体设计来说,剩下一个c将“无家可归”
不过zyh和wp大佬指出,在优化的华莱士树设计中并不用考虑这个进位位c的情况,即最低位的华莱士树部件的进位输入直接接0即可,这样一来两个“错误的华莱士树”并没有错。具体放到下个小节讨论
现在可以知道书中两个错误的华莱士树错误的共同之处在于进位位的位数。另外书中似乎并没有细说的是两个错误的华莱士树的错误也有不同之处:关键点在于延迟。
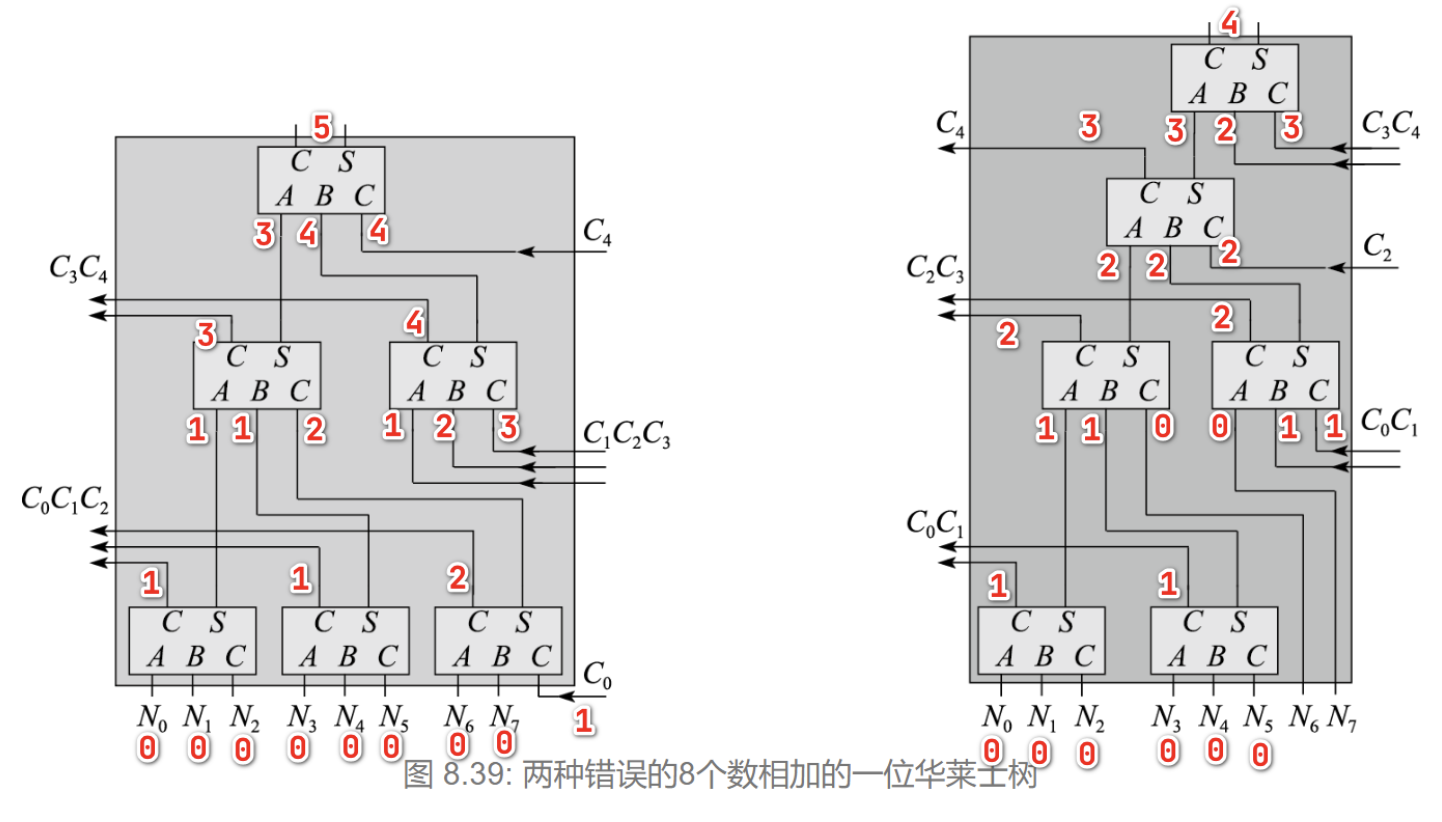
图来自zyh大佬,图中红色数字为部件单位延迟,即经过一个CSA延迟+1,可以看到由于左边的华莱士树将低位进位C0与0延迟的原始输出相加,使得输出结果延迟为2,并一路导致最终输出的延迟为5,相比右边的华莱士树与“正确的华莱士树”只有4的延迟,虽然输出并没有错误,但因为延迟问题导致这种结构注定是要被抛弃的,因此是错误的!
粗略总结华莱士树在多个数相加时相比使用多个加法器的优势。用上面4个4位数相加举例:

4个4位数相加使用了两层CSA,第一层CSA的进位位传递到了第二层,因此第一层相邻的cin和cout之间没有依赖关系,全加器的S输出需要3级门延迟,C输出需要2级门延迟,因此不论参与加法的数据宽度是多少位,将4个数相加转换为两个数相加最多只需要6级门延迟。因此可知,无论数据宽度如何增长,由于每层的CSA的输出延迟都是固定的,因此当数据宽度越宽,CSA的数量呈线性增长,而延迟不变;反观加法器如果要保持延迟不变,比如CLA,那么硬件数量就会指数增长,否则就会增大延迟。
优化的华莱士树乘法器
本节参考自[一生一芯视频号](【功能单元设计 [第五期“一生一芯”计划 - P20]】 【精准空降到 1:08:45】 https://www.bilibili.com/video/BV1ET411m7cZ/?share_source=copy_web&vd_source=c0d41b92058c38bc23233feb8c73c581&t=4125)与香山的乘法器部分。
这里的优化指的是优化Booth的部分积输出:每个Booth编码器输出完整的一个部分积partial,而不用拆成P和c两个部分。这样一来在连接到上层华莱士树以及加法器的时候,就不用考虑进位c的连线,直接将部分积统统输入到华莱士树中即可。因此两个“错误的华莱士树”中,右边的华莱士树其实并没错(左边的依然是因为延迟问题被否决)。
结合视频与代码可以知道,部分积最终被优化成了这个金字塔形(星号部分,每行代表一个部分积),进位位c也被合并到了部分积当中:

本小节到此结束,粗略总结优化的好处在于进位位也合并到了这些部分积中,不用再单独接线,使得后续接入华莱士树在结构上更为灵活,不用再为了与Booth进位位匹配而谨慎设计华莱士树的进位位数。
细节补充
- 香山主要使用5-3压缩器对每列进行压缩(视频中用3-2压缩器举例),当位数不够时退而使用3-2压缩器和2-2压缩器进行压缩。
- 以每次可并行压缩的数作为同一层,并将结果放到下一层。比当前层某列有10个数,可能会分成两组,每组5个并行地进行5-3压缩,并将输出的S和C放到下一层进行压缩。这样只会在层与层之间产生依赖(下层输入依赖上层输出),可以根据实际情况在层与层之间加入流水。
- 部分积之所要优化成金字塔形是为了便于减少列压缩次数,省去将一些固定为0的位也加入求和。(与代码实现有关)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号