算法系列:单链表逆序
Copyright © 1900-2016, NORYES, All Rights Reserved.
http://www.cnblogs.com/noryes/
欢迎转载,请保留此版权声明。
---------------------------------------------------------------------------------------
链表定义如下:
typedef struct Node
{
int data;
Node* next;
}Node;
如何在不使用额外存储节点的情况下使一个单链表的所有节点逆序?
1、迭代
我们先用迭代的思想来分析这个问题,链表的初始状态如图(1)所示:
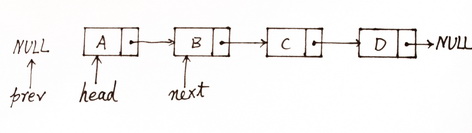
图(1)初始状态
初始状态,prev 是 NULL,head 指向当前的头节点 A,next 指向 A 节点的下一个节点 B。首先从 A 节点开始逆序,将 A 节点的 next 指针指向 prev,因为 prev 的当前值是 NULL,所以 A 节点就从链表中脱离出来了,然后移动 head 和 next 指针,使它们分别指向 B 节点和 B 的下一个节点 C(因为当前的 next 已经指向 B 节点了,因此修改 A 节点的 next 指针不会导致链表丢失)。逆向节点 A 之后,链表的状态如图(2)所示:

图(2)经过第一次迭代后的状态
从图(1)的初始状态到图(2)状态共做了四个操作,这四个操作的伪代码如下:
head->next = prev;
prev = head;
head = next;
next = head->next;
这四行伪代码就是算法的迭代体了,现在用这个迭代体对图(2)的状态再进行一轮迭代,就得到了图(3)的状态:
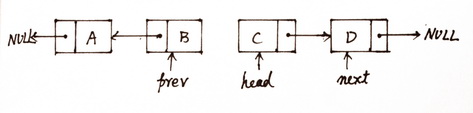
图(3)经过第二次迭代后的状态
那么迭代终止条件呢?现在对图(3)的状态再迭代一次得到图(4)的状态:
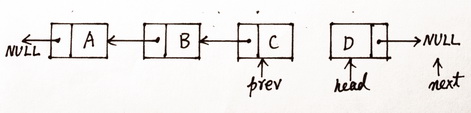
图(4)经过第三次迭代后的状态
此时可以看出,在图(4)的基础上再进行一次迭代就可以完成链表的逆序,因此迭代的终止条件就是当前的 head 指针是 NULL。
现在来总结一下,迭代的初始条件是:
prev = NULL;
迭代体是:
next = head->next;
head->next = prev;
prev = head;
head = next;
迭代终止条件是:
head == NULL;
根据以上分析结果,逆序单链表的迭代算法如下所示:
Node* reverseListIteration(Node* head)
{
Node* prev = NULL;
while (NULL != head)
{
Node* next = head->next;
head->next = prev;
prev = head;
head = next;
}
return prev;
}
2、递归
现在,我们用递归的思想来分析这个问题。先假设有这样一个函数,可以将以 head 为头节点的单链表逆序,并返回新的头节点指针,应该是这个样子:
Node* reverseListRecursion(Node* head);
现在利用 reverseListRecursion 对问题进行求解,将链表分为当前表头节点和其余节点,递归的思想就是,先将当前的表头节点从链表中拆出来,然后对剩余的节点进行逆序,最后将当前的表头节点连接到新链表的尾部。第一次递归调用 reverseListRecursion 函数时的状态如图(5)所示:

图(5)第一次递归状态图
这里边的关键点是头节点 head 的下一个节点 head->next 将是逆序后的新链表的尾节点,也就是说,被摘除的头接点 head 需要被连接到 head->next 才能完成整个链表的逆序,递归算法的核心就是一下几行代码:
newHead = reverseListRecursion(head->next);
head->next->next = head;
head->next = NULL;
现在顺着这个思路再进行一次递归,就得到第二次递归的状态图:
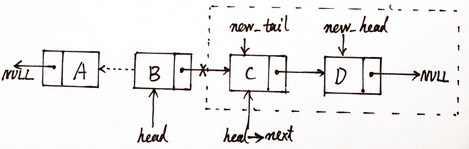
图(6)第二次递归状态图
再进行一次递归分析,就能清楚地看到递归终止条件了:
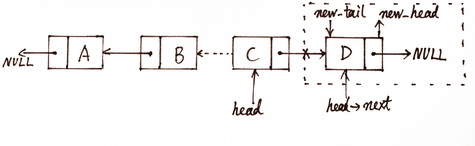
图(7)第三次递归状态图
递归终止条件就是链表只剩一个节点时直接返回这个节点的指针。可以看出这个算法的核心其实是在回溯部分,递归的目的是遍历到链表的尾节点,然后通过逐级回朔将节点的 next 指针翻转过来。
递归算法的完整代码如下:
Node* reverseListRecursion(Node* head)
{
Node* newHead;
if((NULL == head) || (NULL == head->next))
{
return head;
}
newHead = reverseListRecursion(head->next);
head->next->next = head;
head->next = NULL;
return newHead;
}
3、测试
#include <iostream.h>
using namespace std;
int main()
{
Node* pHead = new Node, *pTemp;
pHead->data = 0;
pHead->next = NULL;
for (int i = 1; i < 10; ++i)
{
pTemp = new Node;
pTemp->data = i;
pTemp->next = pHead;
pHead = pTemp;
}
// 打印出原始链表
pTemp = pHead;
cout << "origin:\t\t";
while(pTemp)
{
cout << pTemp->data << ",";
pTemp = pTemp->next;
}
cout << endl;
// 迭代法逆序链表并输出
pHead = reverseListIteration(pHead);
pTemp = pHead;
cout << "reversedByIteration:\t";
while(pTemp)
{
cout << pTemp->data << ",";
pTemp = pTemp->next;
}
cout << endl;
// 递归法逆序链表并输出
pHead = reverseListRecursion(pHead);
pTemp = pHead;
cout << "reversedByRecursion:\t";
while(pTemp)
{
cout << pTemp->data << ",";
pTemp = pTemp->next;
}
cout << endl;
return 0;
}
4、总结
迭代还是递归?这是个问题。当面对一个问题的时候,不能一概认为哪种算法好,哪种不好,而是要根据问题的类型和规模作出选择。对于线性数据结构,比较适合用迭代循环方法,而对于树状数据结构,比如二叉树,递归方法则非常简洁优雅。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号