Math: Fibonacci
https://www.zhihu.com/question/28062458
http://blog.csdn.net/hikean/article/details/9749391
对于Fibonacci数列,1,1,2,3,5,8,13,21...
F(0) = 1, F(1) = 1, F(i) = F(i-1) + F(i-2) 求解第n项。
1、递归
long fib(int n) { if (n == 0 || n == 1) { return 1; }
return fib(n-1) + fib(n-2); }
这是最好写,也是效率最低的方法,时间复杂度是指数级别的。
2、遍历
long fib(int n) { if (n == 0 || n == 1) { return 1; }
vector <long> fibs(2, 1); for (int i = 2; i <= n; ++i) { fibs.push_back(fibs[i-1] + fibs[i-2]); }
return fibs[n]; }
这个方法也是很容易想到的,时间复杂度是 O(n), 空间复杂度也是 O(n)。
3、遍历优化版
fibs[n]只和前两个元素相关,因此任意时刻我们只要有前两项就可以了。这样空间复杂度可以做到 O(1),我们用个循环数组就可以了。
long fib(int n) { if (n == 0 || n == 1) { return 1; } int fib[3]; fib[0] = fib[1] = 1; int idx = 1; for (int i = 2; i <= n; ++i) { idx = (idx + 1) % 3; fib[idx] = fib[(idx + 2)%3] + fib[(idx + 1)%3]; }
return fib[idx]; }
4、矩阵相乘
把一维问题拉到二维。

所以,

现在问题是如何快速计算一个矩阵的n次方。这里可以利用A^n = A^(n/2)*A^(n/2) * (n % 2 == 1 ? A : I)进行分治。
matrix power(matrix A, int n) { matrix ans = I; while(n > 0) { if (n % 2 == 1) { ans *= A; }
A *= A; n /= 2; }
return ans; }
这个算法的时间复杂度是O(logN).
5、特征值分解
对于矩阵的 n 次方求解,可以通过矩阵的特征值分解来完成。过程如下:

6、差分方程求解
如果了解差分方程,那么这个解析解就很容易得到了。
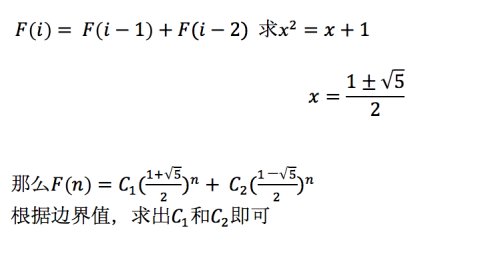
居天下之广居,立天下之正位,行天下之大道,得志与民由之,不得志独行其道,富贵不能淫,贫贱不能移,威武不能屈,此之谓大丈夫。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号