CF519E A and B and Lecture Rooms

题目传送门

这道题目...真是一道好题...题出的好！难度适中！覆盖知识点广！题目有着切合实际的背景！解法比较自然！给出题人点赞 ！

题意：

　　给你一棵树，每次询问给出两个点，问树上有多少点到这两个点的距离相等。

$Sol$


树上距离...嗯肯定有$LCA$，但是看起来还是毫无思路的样子啊...怎么办。

这个时候分类讨论一定是个不错的选择（逃）

 

由于我只会树上倍增，而且大部分时候它还是很好用的，还能求出许多附属需要的东西，所以我们先用树上倍增法求出树上这两点的距离，进行分类讨论。（设置一个a的深度大于b的深度的前提）

1）当距离为奇数：无解，答案为0.

 

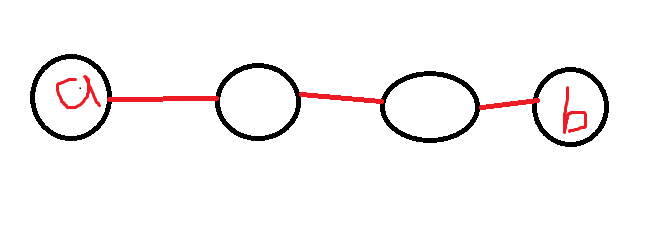
比如答案要求到a和b距离相等的点，ab距离为奇数，显然没有。 

2）当距离为偶数

　·　　a,b在同一条链上。

显然b是a,b的LCA，答案就是a.b节点的中点它所有子树的大小除去有a的那棵子树大小。即$size[中点]-size[中点的a所在子树]$

Explanation：

（开始在这里理解有偏差，ab中点有可能不止a一个子树）。在ab中点的子树上的点到ab中点的过程中，距离是一定的。而ab中点到a,b距离又分别相等，所以距离相等。

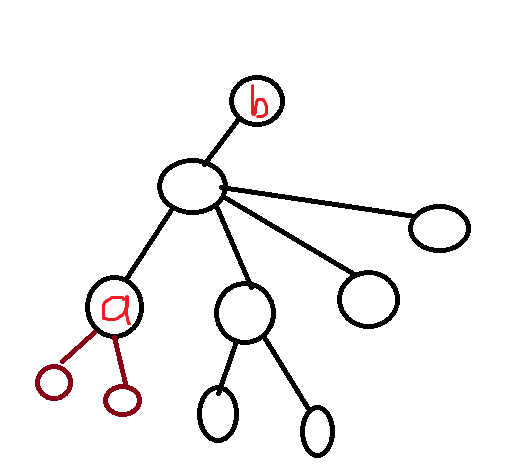
　　·　　a,b分别在他们的LCA两侧，且二者的深度相同。

显然LCA是一个合法的点，而且LCA的祖先们也是合法的点，而且LCA的除a,b所在的所有子树上的所有点也是合法的。（道理同上），答案就是$n-size[lca的a所在子树]-size[lca的b所在子树]$

　　·　　a,b分别在他们的LCA两侧，且二者深度不相同。

有了前面的基础，这里就会好想一点，答案正是$size[mid]-size[mid的子树中有a的那棵]$

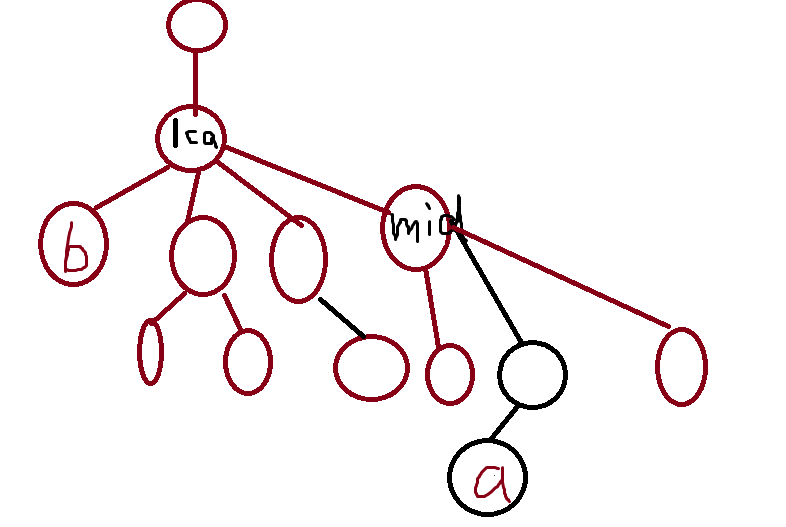
从上面的分析我们也可以看出，我们要求的，也只不过是size，d（深度）。这些在进行倍增预处理时可以顺带求出。然后求“有a的那棵子树”怎么求？我们其实暴力向上倍增一下即可（不是暴力向上跳，是倍增，从大到小缩小范围）。

Code

 

  1 #include<cstdio>
  2 #include<algorithm>
  3 #include<queue>
  4 #include<cmath>
  5 #define maxn 100090
  6 
  7 using namespace std;
  8 
  9 int n,m,tot,t;
 10 int head[maxn],size[maxn],d[maxn];
 11 int f[maxn][30];
 12 bool vis[maxn];
 13 struct node{
 14     int to,next;
 15 }edge[maxn*2];
 16 
 17 void add(int x,int y)
 18 {
 19     edge[++tot].to=y;
 20     edge[tot].next=head[x];
 21     head[x]=tot;
 22 }
 23 
 24 void init_1()
 25 {
 26     queue<int>q;
 27     q.push(1);d[1]=1;
 28     while(!q.empty())
 29     {
 30         int u=q.front();q.pop();
 31         for(int i=head[u];i;i=edge[i].next)
 32         {
 33             int v=edge[i].to;
 34             if(d[v]) continue;
 35             d[v]=d[u]+1;
 36             f[v][0]=u;
 37             for(int j=1;j<=t;j++)
 38                 f[v][j]=f[f[v][j-1]][j-1];
 39             q.push(v);
 40         }
 41     }
 42 }
 43 
 44 void init_2(int u)
 45 {
 46     vis[u]=1;size[u]++;
 47     for(int i=head[u];i;i=edge[i].next)
 48     {
 49         int v=edge[i].to;                               
 50         if(vis[v]) continue;
 51         init_2(v);
 52         size[u]+=size[v];
 53     }
 54 }
 55 
 56 int find(int x,int dep)
 57 {
 58     int hu=x;
 59     for(int i=t;i>=0;i--)
 60     {
 61         if(d[hu]-(1<<i)<dep) continue;
 62         hu=f[hu][i];
 63     }
 64     return hu;
 65 }
 66 
 67 int ask(int x,int y)
 68 {
 69     if(d[x]<d[y]) swap(x,y);
 70     int prex=x,prey=y,lca=0,tmp=0;
 71     for(int i=t;i>=0;i--)
 72         if(d[f[x][i]]>=d[y]) x=f[x][i];
 73     if(x==y) lca=x;
 74     else
 75     {
 76         for(int i=t;i>=0;i--)
 77             if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
 78         lca=f[x][0];
 79     }
 80     x=prex,tmp=y,y=prey;
 81     int dis=d[x]+d[y]-2*d[lca];
 82     if(dis&1) return 0;
 83     if(lca==y)
 84     {
 85         int mid=(d[x]+d[y])>>1;
 86         return size[find(x,mid)]-size[find(x,mid+1)];
 87     }
 88     else 
 89     {
 90         if(d[x]==d[y])
 91             return n-size[find(x,d[lca]+1)]-size[find(y,d[lca]+1)];        
 92         else 
 93         {
 94             int mid=d[x]-(dis>>1);
 95             return size[find(x,mid)]-size[find(x,mid+1)];
 96         }
 97     }
 98 }
 99 
100 int main()
101 {
102     scanf("%d",&n);
103     t=log2(n)+1;
104     for(int i=1;i<=n-1;i++)
105     {
106         int x=0,y=0;
107         scanf("%d%d",&x,&y);
108         add(x,y);add(y,x);
109     }
110     init_1();
111     init_2(1);
112     scanf("%d",&m);
113     for(int i=1;i<=m;i++)
114     {
115         int x=0,y=0;
116         scanf("%d%d",&x,&y);
117         if(x==y){printf("%d\n",n);continue;}
118         printf("%d\n",ask(x,y));
119     }
120     return 0;
121 }
View Code

 

参考文献：https://www.cnblogs.com/qixingzhi/p/9302038.html（从这里学会的）

 

posted @ 2018-09-29 10:43  cellur925&Chemist  阅读(298)  评论(0)  编辑  收藏  举报