LuoguP1606 [USACO07FEB]荷叶塘Lilypad Pond 【最短路】By cellur925

最短路好题！】

参考资料：学长 https://blog.csdn.net/TSOI_Vergil/article/details/52975779 学长太强了！！！%%%

题目传送门

==================算法部分=====================

我们读完题后，就能感受到浓浓的最短路氛围。我们可以将水与莲花间连边，水水间连边，边权为1；莲花间各自连边，边权为0。这样我们跑完一遍spfa后，就能得到摆放莲花的最小数量。但是第二问就很棘手，聪明的你也许会说跑一遍最短路计数就行了。但其实这是错误的算法。

比如在这张图中。正方形是莲花，圆是水（后连的莲花）

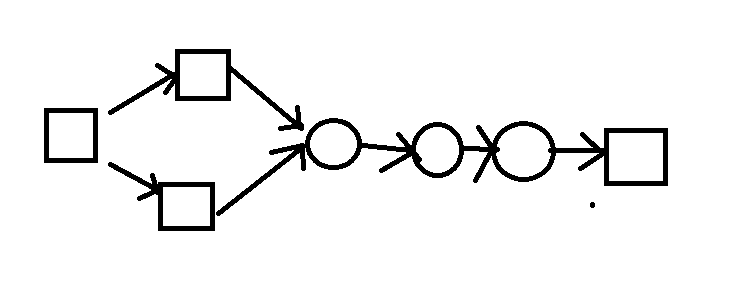
最短路条数为2，但有3个莲花。

或者更理性的说，如果经过的水面相同而经过的莲花不同，会被算作是不同的最短路，而实际上方案却是一样的。

不同的最短路要求很低，只要经过的点有一点不同便不同。而适合本题的求解则是只能水面不同，已有的莲花不同不算不同，也就是说 跑最短路时只经过水面。

再冷静分析我们会发现已有的莲花间的边是无意义的，只是“为了保证连通性”。同理，除起点和终点外的莲花与水之间的边也是没有意义的。

所以 我们考虑重新建图，对于每个水，对它进行bfs，把它和它能到达的水连边（或作可达性标记）；将起点终点与水连边，这样跑最短路 。我们发现经过这样建图后最短路上的点除起点和终点是莲花之外，其余的点全是水，这样不同的最短路就对应着经过了不同的水，也就对应着不同的放莲花的方案。

以上有很多都参考Vergil学长的分析==

 

==================代码实现部分========================

然而算法说起来简单，实现就有些难了。学长给出的代码我太弱不能理解，于是便参考了金涛dalao的写法。从他的代码中对搜索有了更深理解。

先来观摩一下学长的代码，比较妙的地方是把矩阵的横纵坐标压成序号。

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

#define maxn 130005

int n,m,g[35][35],sx,tx,sy,ty,l,cnt;

int pre[maxn],last[maxn],other[maxn];

int quex[1000000],quey[1000000],que[1000000];

const int dx[9]={0,1,1,2,2,-1,-1,-2,-2};

const int dy[9]={0,-2,2,-1,1,-2,2,-1,1};

int flag[35][35],dis[1005];

bool vis[1005][1005],vist[maxn];

long long f[1005];

 

void connect(int x,int y)

{

    l++;

    pre[l]=last[x];

    last[x]=l;

    other[l]=y;    

}

 

void bfs(int fx,int fy)

{

    flag[fx][fy]=++cnt;

    int h=1,t=0;

    for (int i=1;i<=8;i++) 

    {

        int xx=fx+dx[i];

        int yy=fy+dy[i];

        if (xx<1||xx>n||yy<1||yy>m) continue;

        if (flag[xx][yy]==cnt) continue;

        flag[xx][yy]=cnt;

        if (g[xx][yy]!=2&&g[xx][yy]!=0) 

        {

            t++;

            quex[t]=xx;quey[t]=yy;

            int id1=(fx-1)*m+fy;

            int id2=(xx-1)*m+yy;

            if (vis[id1][id2]) continue;

            connect(id1,id2);

            connect(id2,id1);

            vis[id1][id2]=vis[id2][id1]=1;    

        }

        else if (g[xx][yy]==0)     

        {

            int id1=(fx-1)*m+fy;

            int id2=(xx-1)*m+yy;

            if (vis[id1][id2]) continue;

            connect(id1,id2);

            connect(id2,id1);

            vis[id1][id2]=vis[id2][id1]=1;    

        }

    }

    while (h<=t) 

    {

        int x=quex[h],y=quey[h];h++;

        for (int i=1;i<=8;i++) 

        {

            int xx=x+dx[i];

            int yy=y+dy[i];

            if (xx<1||xx>n||yy<1||yy>m) continue;

            if (flag[xx][yy]==cnt) continue;

            flag[xx][yy]=cnt;

            if (g[xx][yy]==0) 

            {

                int id1=(fx-1)*m+fy;

                int id2=(xx-1)*m+yy;

                if (vis[id1][id2]) continue;

                connect(id1,id2);

                connect(id2,id1);

                vis[id1][id2]=vis[id2][id1]=1;

            }

            else if (g[xx][yy]!=2&&g[xx][yy]!=0) 

            {

                t++;

                quex[t]=xx;quey[t]=yy;    

            }

        }

    }

}

 

void spfa(void)

{

    memset(dis,53,sizeof dis);

    dis[(sx-1)*m+sy]=0;

    que[1]=(sx-1)*m+sy;

    int h=1,t=1;

    while (h<=t) 

    {

        int u=que[h];h++;

        vist[u]=0;

        for (int p=last[u];p;p=pre[p]) 

        {

            int v=other[p];

            if (dis[v]>dis[u]+1) 

            {

                dis[v]=dis[u]+1;    

                if (!vist[v]) 

                {

                    que[++t]=v;

                    vist[v]=1;    

                }

            }

        }

    }

}

 

void solve(void)

{

    memset(vist,0,sizeof vist);

    que[1]=(sx-1)*m+sy;f[que[1]]=1;

    int h=1,t=1;

    while (h<=t) 

    {

        int u=que[h];h++;

        for (int p=last[u];p;p=pre[p]) 

        {

            int v=other[p];

            if (dis[v]==dis[u]+1) 

            {

                f[v]+=f[u];

                if (!vist[v]) 

                {

                    que[++t]=v;

                    vist[v]=1;    

                }

            }

        }

    }

}

 

int main()

{

    scanf("%d%d",&n,&m);

    for (int i=1;i<=n;i++) 

        for (int j=1;j<=m;j++) 

        {

            scanf("%d",&g[i][j]);

            if (g[i][j]==3) {sx=i;sy=j;}

            if (g[i][j]==4) {tx=i;ty=j;}

        }

    bfs(sx,sy);

    bfs(tx,ty);

    for (int i=1;i<=n;i++) 

        for (int j=1;j<=m;j++) 

            if (g[i][j]==0) bfs(i,j);

    spfa();

    if (dis[(tx-1)*m+ty]>1e7) 

    {

        printf("-1\n");

        return 0;

    }

    printf("%d\n",dis[(tx-1)*m+ty]-1);

    solve();

    printf("%lld\n",f[(tx-1)*m+ty]);

    return 0;    

}

金涛的代码就比较亲民了Orz。我仿照他的代码写了一份。注释里有解释。

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#include<utility>

using namespace std;
typedef long long ll;

int n,m,bx,by,ex,ey;
int mapp[40][40],dis[40][40];
ll f[40][40];//记得开long long！！
bool vis[40][40];
bool able[40][40][40][40];
int dx[20]={0,1,2,2,1,-1,-2,-2,-1};
int dy[20]={0,-2,-1,1,2,2,1,-1,-2};

void floodfill(int x,int y)
{//洪水填充，也可以理解为bfs
    memset(vis,0,sizeof(vis));
    queue<pair<int,int> > q;
    q.push(make_pair(x,y));
    while(!q.empty())
    {
        int nowx=q.front().first;
        int nowy=q.front().second;
        q.pop();
        for(int i=1;i<=8;i++)
        {
            int xx=nowx+dx[i];
            int yy=nowy+dy[i];
            if(xx<1||xx>n||yy<1||yy>m) continue;
            if(vis[xx][yy]) continue;//vis数组实际在检查是不是莲花，但我们要找水
            if(!mapp[xx][yy]||(xx==ex&&yy==ey))
                able[x][y][xx][yy]=1;//注意是x,y 我们洪水填充的目的是更新传进的x,y
// able相当于连边了 效果一样
            else if(mapp[xx][yy]==1)
                q.push(make_pair(xx,yy)),vis[xx][yy]=1; 
//如果是莲花，就是待扩展节点，加入队列
        }
    }
}

void spfa_work()
{//边跑最短路边计数
    memset(vis,0,sizeof(vis));
    queue<pair<int,int> >q;
    q.push(make_pair(bx,by));
    memset(dis,127,sizeof(dis));
    vis[bx][by]=1;dis[bx][by]=0,f[bx][by]=1;
    while(!q.empty())
    {
        int nowx=q.front().first;
        int nowy=q.front().second;
        q.pop();vis[nowx][nowy]=0;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                if(able[nowx][nowy][i][j])
                {
                    if(dis[i][j]>dis[nowx][nowy]+1)
                    {
                        dis[i][j]=dis[nowx][nowy]+1;
                        f[i][j]=f[nowx][nowy];
                        if(!vis[i][j]&&(i!=ex||j!=ey))
                        {//终点就不用再扩展了
                            vis[i][j]=1;
                            q.push(make_pair(i,j));
                        }
                    }
                    else if(dis[i][j]==dis[nowx][nowy]+1)
                        f[i][j]+=f[nowx][nowy];
                }
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&mapp[i][j]);
            if(mapp[i][j]==3) bx=i,by=j;
            if(mapp[i][j]==4) ex=i,ey=j; 
        }
    floodfill(bx,by);
//从起点出发
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(!mapp[i][j]) floodfill(i,j);
    spfa_work();
    if(dis[ex][ey]>1000) 
    {//最多也才900个点
        printf("-1");
        return 0;
    } 
    else printf("%d\n%lld",dis[ex][ey]-1,f[ex][ey]);
//注意-1 以及lld
    return 0;
}

 

 

在这道题中学到了肥肠多的新想法，更深入理解了搜索算法。

本来最简单的dfsbfs我是不会的，但是学习了图论之后，就能感性理解，现在我们回过头去看那些最简单的：

bfs 我们常常使用队列实现，而我们要注意到，队列中的点都是待扩展节点。每次我们取出队头的顶点，遍历它能到达的全部状态。