[POI2008]BLO-Blockade 【无向图tarjan/鸽点】By cellur925

题目传送门

lyd无向图tarjan的例题。

一句话题意（不得不佩服lyd老师的高度概括能力）：在一张无向连通图上，求出每个点被破坏（去掉与这个点相关的所有边，不去掉这个点）后，无向图中使i,j不连通有序点对（i，j）个数。

 

浓浓的鸽点气息。

但是这题又不单单是鸽点。

 

我们冷静分析，分类讨论（分类讨论这个美好的品质常被oier所忽略）

每个点有两种类型：是鸽点/不是鸽点

一、不是鸽点

　　那么去掉这个点所连的所有边后，只有这个点和剩下的点不连通，而其他点还联系的好好地，所以答案即为2*(n-1)，由于是无序点对，所以乘2.

二、是鸽点

　　那么图会分裂成几个联通块，答案是这几个联通块的大小两两相乘再相加。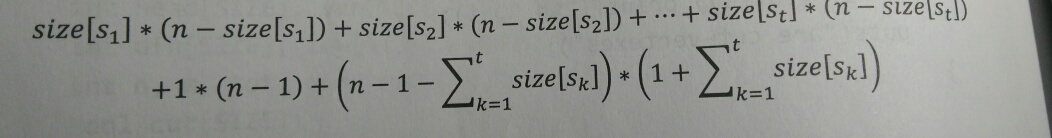

我真懒，真的。

size[i]表示以i为根的子树大小。我们可以在tarjan跑鸽点的时候顺便求出。

大体思路就是这样，还是比较简单易懂的。

Code

#include<cstdio>
#include<algorithm>

using namespace std;
typedef long long ll;

int n,m,tot,num;
int head[100090],dfn[100090],low[100090];
bool cut[100090];
ll size[100090],ans[100090];
struct node{
    int to,next;
}edge[1000090];

void add(int x,int y)
{
    edge[++tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}

void tarjan(int x)
{
    dfn[x]=low[x]=++num;size[x]=1;
    int flag=0;ll sigma=0;
    for(int i=head[x];i;i=edge[i].next)
    {
        int y=edge[i].to;
        if(!dfn[y])
        {
            tarjan(y);
            size[x]+=size[y];
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x])
            {
                flag++;
                ans[x]+=1ll*size[y]*(n-size[y]);
                sigma+=size[y];
                if(x!=1||flag>1) cut[x]=true;
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
    if(cut[x])//是鸽点 
        ans[x]+=1ll*(n-sigma-1)*(1+sigma)+(n-1);
    else //不是鸽点 
        ans[x]=1ll*2*(n-1);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x=0,y=0;
        scanf("%d%d",&x,&y);
        if(x==y) continue;
        //去掉自环 
        add(x,y);
        add(y,x);
    }
    tarjan(1);
    //图保证联通。只调用一次便足够。
    //意念起点为1 
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}