Luogu P1970 花匠 【线性Dp】 By cellur925

题目描述 Description

花匠栋栋种了一排花，每株花都有自己的高度。花儿越长越大，也越来越挤。栋栋决定把这排中的一部分花移走，将剩下的留在原地，使得剩下的花能有空间长大，同时，栋栋希望剩下的花排列得比较别致。
具体而言，栋栋的花的高度可以看成一列整数h_1, h_2, … , h_n。设当一部分花被移走后，剩下的花的高度依次为g_1, g_2, … , g_m，则栋栋希望下面两个条件中至少有一个满足：
条件 A：对于所有的1<i<m/2，g_2i > g_2i-1，且g_2i > g_2i+1； 
条件 B：对于所有的1<i<m/2，g_2i < g_2i-1，且g_2i < g_2i+1。
注意上面两个条件在m = 1时同时满足，当m > 1时最多有一个能满足。
请问，栋栋最多能将多少株花留在原地。

输入描述 Input Description

输入的第一行包含一个整数 n，表示开始时花的株数。
第二行包含 n 个整数，依次为h_1, h_2,… , h_n，表示每株花的高度。

输出描述 Output Description

输出一行，包含一个整数 m，表示最多能留在原地的花的株数。

样例输入 Sample Input

5 
5 3 2 1 2

样例输出 Sample Output

3

数据范围及提示 Data Size & Hint

对于 20%的数据，n ≤ 10； 
对于 30%的数据，n ≤ 25； 
对于 70%的数据，n ≤ 1000，0 ≤ h_i ≤ 1000； 
对于 100%的数据，1 ≤ n ≤ 100,000，0 ≤ h_i ≤ 1,000,000，所有的h_i随机生成，所有随机数服从某区间内的均匀分布。

 

这个题..其实挺难读懂的。我们只要手动模拟一下就会发现，合法的序列是一个抖动序列，也就是这样的

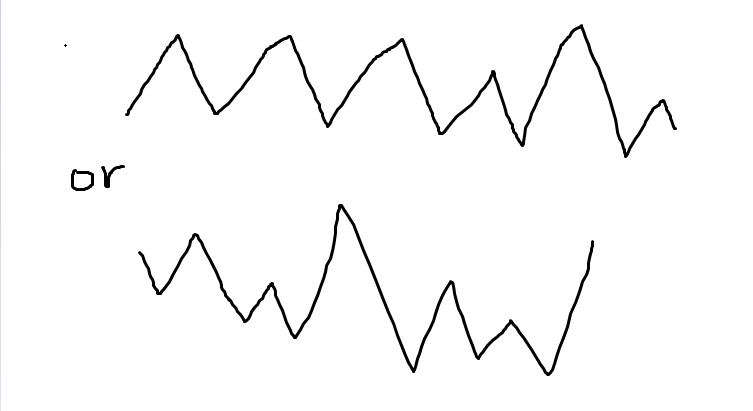
那么状态也就好设计了。

显然有

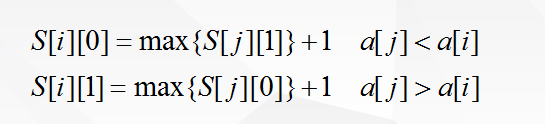
然而这个转移是O（n^2）的，我们能不能进行一下优化？

再仔细搞一搞，我们就会（kantijie）发现，当前的状态只与上一个状态有关：我们还是冷静分析一下。

我们每次转移都要努力做到最优，不妨先认为上一个为最优。

等等，这怎么和LIS有些像？但是这样的优化并不适用于LIS啊！然而，我们在求LIS时，总是（小贪心地）想保留最小的值，以赌到更长的上升子序列，而本题就不用。只要当前的比之前的高或者矮，不管高多少、矮多少，都是优解。所以这个策略是正确的。

（可能证明的并不严密

code

#include<cstdio>
#include<algorithm>

using namespace std;

int n;
int s[100090][2];
int a[100090];

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    s[1][0]=s[1][1]=1;
    for(int i=2;i<=n;i++)
    {
        s[i][0]=s[i-1][0];s[i][1]=s[i-1][1];
         if(a[i]>a[i-1])
          s[i][0]=s[i-1][1]+1;
         if(a[i]<a[i-1])
          s[i][1]=s[i-1][0]+1;
    }
    printf("%d",max(s[n][1],s[n][0]));
    return 0;
}