LuoguP1314 聪明的质检员 【二分答案/前缀和】
美丽的题号预示着什么...
描述
小 T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有n个矿石,从1到n逐一编号,每个矿石都有自己的重量wi以及价值vi。检验矿产的流程是:
1、给定m个区间[Li,Ri];
2、选出一个参数W;
3、对于一个区间[Li,Ri],计算矿石在这个区间上的 检验值Yi:
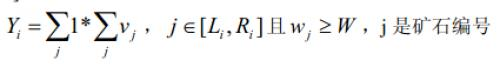
这批矿产的 检验结果Y 为各个区间的检验值之和 。即: Y1+Y2...+Ym
若这批矿产的 检验结果 与所给标准值S相差太多,就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产,所以他想通过调整参数W的值,让 检验结果 尽可能的靠近标准值S,即使得 S-Y 的绝对值最小。请你帮忙求出这个最小值。
格式
输入格式
第一行包含三个整数n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的n行,每行2个整数,中间用空格隔开,第i+1行表示i号矿石的重量wi和价值vi 。
接下来的m行,表示区间,每行2个整数,中间用空格隔开,第i+n+1行表示区间[Li,Ri]的两个端点Li和Ri。 注意:不同区间可能重合或相互重叠。
输出格式
输出只有一行,包含一个整数,表示所求的最小值。
样例1
样例输入1
5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3样例输出1
10
提示
样例说明:当W选4的时候,三个区间上检验值分别为20、5、0,这批矿产的检验结果为25,此时与标准值S相差最小为10。
对于10%的数据,有1 ≤ n,m ≤ 10;
对于30%的数据,有1 ≤ n,m ≤ 500;
对于50%的数据,有1 ≤ n,m ≤ 5,000;
对于70%的数据,有1 ≤ n,m ≤ 10,000;
对于100%的数据,有1 ≤ n,m ≤ 200,000,0 < wi, vi ≤ 10^6,0 < S ≤ 10^12,1 ≤ Li ≤ Ri ≤ n。
来源
NOIp2011提高组Day2第二题
这道题...题面读了好久(晦涩难懂)
做背包做惯了于是以下及我的代码把数组v与w的意义调换了一下(v为重量,w为价值)
因为参数值W是不固定的,而且坐落在有序的一段区间上(1~max v[i] ),所以我们可以愉快地使用二分答案。
如果我们二分出的这个参数值使得Y较小,说明参数取得有些大,满足的值很少,我们向左移一移。
如果我们二分出的这个参数值使得Y较大,说明参数取得有些小,满足的值很多,我们向右移一移。
根据lyd老师的指引,我们愉快地写出了二分答案的代码
int l=1,r=mx; while(l<r) { int mid=(l+r+1)>>1; Y=check(mid); if(Y<s) r=mid-1; else l=mid; ans=min(ans,abs(s-Y)); }
接下来就是check函数的写法。
由于数据达到了1e6,我们肯定不能暴力计算区间和,前缀和坠吼了。
ll check(int x) { ll tmp=0; for(int i=1;i<=n;i++) { sum[i]=sum[i-1]; cnt[i]=cnt[i-1]; if(v[i]>=x) { sum[i]+=w[i]; cnt[i]++; } } for(int i=1;i<=m;i++) tmp+=(sum[q[i].second]-sum[q[i].first-1])*(cnt[q[i].second]-cnt[q[i].first-1]); return tmp; }
于是我们就愉快地AC了。
code

1 #include<cstdio> 2 #include<algorithm> 3 #include<utility> 4 #define inf (1LL<<60) 5 6 using namespace std; 7 typedef long long ll; 8 9 int n,m,mx; 10 int v[200009],w[200009]; 11 ll ans=inf,s,Y,sum[200009],cnt[200009]; 12 pair<int,int> q[200009]; 13 /*ll check(int x) 14 { 15 ll tmp=0; 16 for(int i=1;i<=m;i++) 17 { 18 int pos=lower_bound(v+1,v+n+1,x)-v; 19 if(pos>q[i].second) continue; 20 int cnt=max(pos,q[i].first); 21 tmp+=(w[q[i].second]-w[cnt-1])*(q[i].second-cnt+1); 22 } 23 return tmp; 24 }*/ 25 ll check(int x) 26 { 27 ll tmp=0; 28 for(int i=1;i<=n;i++) 29 { 30 sum[i]=sum[i-1]; 31 cnt[i]=cnt[i-1]; 32 if(v[i]>=x) 33 { 34 sum[i]+=w[i]; 35 cnt[i]++; 36 } 37 } 38 for(int i=1;i<=m;i++) 39 tmp+=(sum[q[i].second]-sum[q[i].first-1])*(cnt[q[i].second]-cnt[q[i].first-1]); 40 return tmp; 41 } 42 int main() 43 { 44 scanf("%d%d%lld",&n,&m,&s); 45 for(int i=1;i<=n;i++) 46 scanf("%d%d",&v[i],&w[i]),mx=max(mx,v[i]); 47 for(int i=1;i<=m;i++) 48 scanf("%d%d",&q[i].first,&q[i].second); 49 /* sort(a+1,a+n+1,cmp);*/ 50 /* sum[1]=a[1].w; 51 for(int i=2;i<=n;i++) 52 sum[i]=sum[i-1]+a[i].w;*/ 53 54 int l=1,r=mx; 55 while(l<r) 56 { 57 int mid=(l+r+1)>>1; 58 Y=check(mid); 59 if(Y<s) r=mid-1; 60 else l=mid; 61 ans=min(ans,abs(s-Y)); 62 } 63 printf("%lld",ans); 64 return 0; 65 }
几个注意事项
§ 虽说没有负数的情况,但是ans初值本身开始也要赋得很大,否则会输出0. (因为这调了很久qaq),ans是long long类型,怎么赋初值?hzwer大神给了一个不错的写法
#define inf (1LL<<60)
§ 开始想排一遍序,然后前缀和直接调用就好了。然而...并没有注意到还有区间下标的限制,还是老实做吧orz!


