Luogu P3320 [SDOI2015]寻宝游戏 / 异象石 【LCA/set】
期末考试结束祭!
在期末考试前最后一发的测试中,异象石作为第二道题目出现QAQ。虽然知道是LCA图论,但还是敲不出来QAQ。
花了两天竞赛课的时间搞懂(逃
异象石
(stone.pas/c/cpp)
题目描述
Adera 是 Microsoft 应用商店中的一款解谜游戏。
异象石是进入 Adera 中异时空的引导物,在 Adera 的异时空中有一张地图。这张地图上
有 N 个点,有 N-1 条双向边把它们连通起来。起初地图上没有任何异象石,在接下来的 M
个时刻中,每个时刻会发生以下三种类型的事件之一:
1. 地图的某个点上出现了异象石(已经出现的不会再次出现);
2. 地图某个点上的异象石被摧毁(不会摧毁没有异象石的点);
3. 向玩家询问使所有异象石所在的点连通的边集的总长度最小是多少。
请你作为玩家回答这些问题。
输入格式
第一行有一个整数 N,表示点的个数。
接下来 N-1 行每行三个整数 x,y,z,表示点 x 和 y 之间有一条长度为 z 的双向边。
第 N+1 行有一个正整数 M。
接下来 M 行每行是一个事件,事件是以下三种格式之一:
+ x 表示点 x 上出现了异象石
- x 表示点 x 上的异象石被摧毁
输出格式
对于每个?事件,输出一个整数表示答案。
样例输入
6
1 2 1
1 3 5
4 1 7
4 5 3
6 4 2
10
+ 3
+ 1
?
+ 6
?
+ 5
?
- 6
- 3
?
样例输出
5
14
17
10
数据范围与约定
对于 30%的数据,1 ≤ n, m ≤ 1000。
对于另 20%的数据,地图是一条链,或者一朵菊花。
对于 100%的数据,1 ≤ n, m ≤ 105, 1 ≤ x, y ≤ n, x ≠ y, 1 ≤ z ≤ 109。
我们先来考虑简单的情况。处理出每个点到树根的距离d[]后,如果此时地图上有两个点,那么使它们联通所需的边集总长度最小即为
d[x]+d[y]-2*d[LCA(x,y)]
这也是树上两点路径的算法。QAQ。
静态的还好说,可是这里是动态维护的,中间既有可能新加石头,也可能移走石头。
我们再来看多个石头的情况。
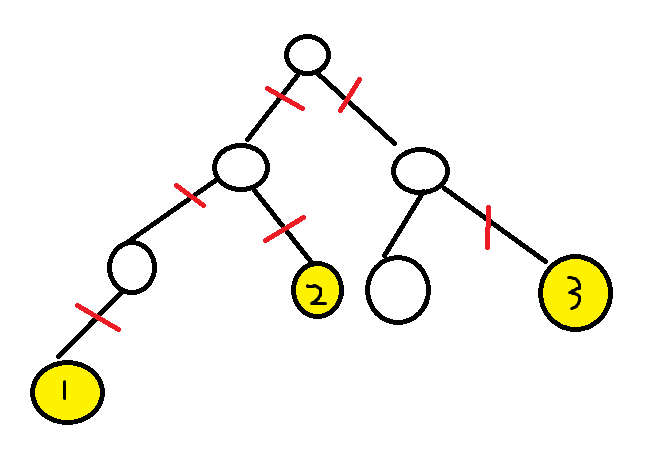
假设黄色是异象石,那么我们要求的就是标红边的线。(从此处开始,对LCA(x,y)的叙述就是x,y两点的距离 ) 那么标红边的线就是
LCA(1,2)+LCA(2,3)+LCA(3,1)的1/2,LCA(1,2)+LCA(2,3)+LCA(3,1)即为寻宝游戏的答案。
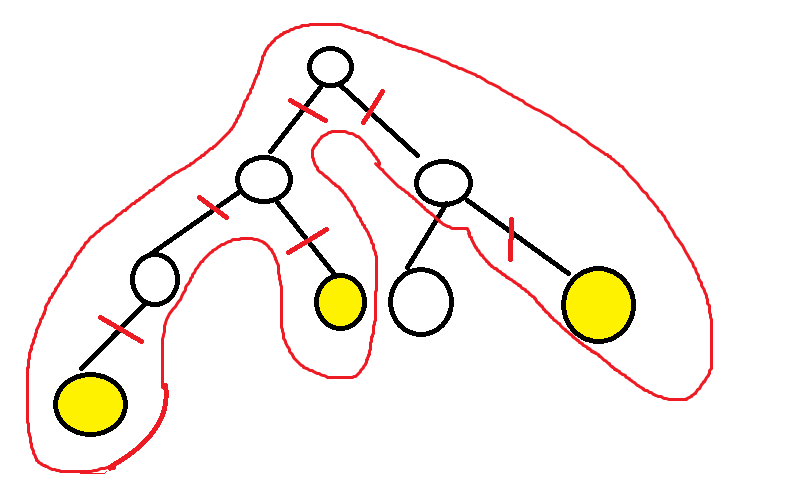
也就是图中被红圈包围起来边权的1/2啦 QAQ。
画再复杂一点的图我们不难发现我们求得,答案就是相邻节点路径之和,头尾也算相邻。
因此我们可以预处理出欲求节点间的最近公共祖先的f数组,还有用倍增思想求出的dis[][],dis[i][j]即为从i节点向上走2^j步的路径权值。
怎么处理相邻呢?这里可以用时间戳和dfs序解决,dfs一遍就可以求得。我们设v[]为时间戳,a[]为dfs序。
理解的话,就是v[i]为第i节点被访问的顺序,a[x]为时间戳为x的节点编号。
另外动态维护的时候可以用到set。对于这么一个高深的stl容器,蒟蒻当然要一番学习。set是一个有序集合,我们还可以利用它的迭代器
(注 :迭代器可以理解成stl里的指针 用iterator声明)
另外我们在返回迭代器时返回的是指针,要真正的那个值就要“解除引用”, 即“ * ”符号
另外set集合里存的是时间戳。
这个地方思维有点混乱QAQ大家可以在代码里看注释,注释里写的很清楚(吧)。
code

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<queue> 6 #include<set> 7 #include<cstring> 8 using namespace std; 9 typedef long long ll; 10 const int MAXN=100090; 11 int y,tot,head[MAXN],n,m,t,f[MAXN][100],visit[MAXN],a[MAXN]; 12 ll ans,d[MAXN],dis[MAXN][100]; 13 struct node{ 14 int to,next; 15 ll val; 16 }edge[2*MAXN]; 17 set<int> s; 18 typedef set<int>::iterator It;// 定义一个迭代器的简称 19 It it;//定义一个迭代器 20 void add(int x,int y,ll z) 21 { 22 edge[++tot].to=y; 23 edge[tot].val=z; 24 edge[tot].next=head[x]; 25 head[x]=tot; 26 } 27 void bfs() 28 { 29 queue<int>q; 30 q.push(1); 31 d[1]=1;visit[1]=1; 32 while(!q.empty()) 33 { 34 int x=q.front(); 35 q.pop(); 36 for(int i=head[x];i;i=edge[i].next) 37 { 38 int y=edge[i].to; 39 if(!visit[y]) 40 { 41 q.push(y);visit[y]=1; 42 d[y]=d[x]+1; 43 f[y][0]=x,dis[y][0]=edge[i].val; 44 for(int j=1;j<=t;j++) 45 {//预处理出倍增思想的f数组和dis数组 46 f[y][j]=f[f[y][j-1]][j-1]; 47 dis[y][j]=dis[f[y][j-1]][j-1]+dis[y][j-1]; 48 } 49 } 50 } 51 } 52 } 53 void dfs(int x) 54 {//求出时间戳和dfs序,visit[]此时的作用是时间戳,a[]的作用是dfs序 55 visit[x]=++tot;a[tot]=x; 56 for(int i=head[x];i;i=edge[i].next) 57 if(!visit[edge[i].to]) dfs(edge[i].to); 58 } 59 inline It L(It it) 60 {// s.end()返回集合中最大元素的下一个位置的迭代器 61 if(it==s.begin()) return --s.end(); 62 return --it; //直接减即可 因为在没有insert()之前,新加入的异象石的左右相邻节点是相邻的! 63 } 64 inline It R(It it) 65 { 66 if(it==--s.end()) return s.begin(); 67 return ++it; 68 } 69 ll LCA(int x,int y) 70 { 71 ll ans=0; 72 if(d[x]>d[y]) swap(x,y); 73 for(int i=t;i>=0;i--) 74 if(d[f[y][i]]>=d[x]) ans+=dis[y][i],y=f[y][i]; 75 if(x==y) return ans; 76 for(int i=t;i>=0;i--) 77 if(f[x][i]!=f[y][i]) ans+=dis[x][i]+dis[y][i],x=f[x][i],y=f[y][i]; 78 return ans+dis[x][0]+dis[y][0]; 79 } 80 int main() 81 { 82 freopen("stone.in","r",stdin); 83 freopen("stone.out","w",stdout); 84 scanf("%d",&n);t=log2(n)+1; 85 for(int i=1;i<=n-1;i++) 86 { 87 int x=0,y=0; 88 ll z=0; 89 scanf("%d%d%lld",&x,&y,&z); 90 add(x,y,z); 91 add(y,x,z); //建图 92 } 93 bfs();//预处理 94 memset(visit,0,sizeof(visit)); tot=0;//注意清零! visit数组前后意义不一样了 95 dfs(1); 96 scanf("%d",&m); 97 for(int i=1;i<=m;i++) 98 { 99 int x=0; 100 char ch; 101 cin>>ch; 102 if(ch=='+') 103 {//改变一个异象石时 需要来考虑和它左边相邻的,右边相邻的 104 scanf("%d",&x); 105 if(s.size()) 106 { 107 it=s.lower_bound(visit[x]);//找出与它右相邻的 108 if(it==s.end()) it=s.begin();//特殊情况的处理 109 y=*L(it);//找它的左相邻 110 ans+=LCA(x,a[y])+LCA(x,a[*it])-LCA(a[y],a[*it]); 111 //加上到左端点、右端点的距离,再减去左右端点互达的距离 112 } 113 s.insert(visit[x]);//set里面存的是时间戳 114 } 115 if(ch=='-') 116 {//set中元素一定不为空 117 scanf("%d",&x); 118 it=s.find(visit[x]); 119 y=*L(it),it=R(it);//同理,找出他当前的左右相邻节点 120 ans-=LCA(x,a[y])+LCA(x,a[*it])-LCA(a[y],a[*it]); 121 s.erase(visit[x]); 122 } 123 if(ch=='?') printf("%lld\n",ans/2); 124 } 125 return 0; 126 }
寻宝游戏和这道题本质是一样的,只需稍加改动,无伤大雅。
code

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<queue> 6 #include<set> 7 #include<cstring> 8 using namespace std; 9 typedef long long ll; 10 const int MAXN=100090; 11 int y,tot,head[MAXN],n,m,t,f[MAXN][100],visit[MAXN],a[MAXN]; 12 ll ans,d[MAXN],dis[MAXN][100]; 13 struct node{ 14 int to,next; 15 ll val; 16 }edge[2*MAXN]; 17 set<int> s; 18 typedef set<int>::iterator It; 19 It it; 20 void add(int x,int y,ll z) 21 { 22 edge[++tot].to=y; 23 edge[tot].val=z; 24 edge[tot].next=head[x]; 25 head[x]=tot; 26 } 27 void bfs() 28 { 29 queue<int>q; 30 q.push(1); 31 d[1]=1;visit[1]=1; 32 while(!q.empty()) 33 { 34 int x=q.front(); 35 q.pop(); 36 for(int i=head[x];i;i=edge[i].next) 37 { 38 int y=edge[i].to; 39 if(!visit[y]) 40 { 41 q.push(y);visit[y]=1; 42 d[y]=d[x]+1; 43 f[y][0]=x,dis[y][0]=edge[i].val; 44 for(int j=1;j<=t;j++) 45 { 46 f[y][j]=f[f[y][j-1]][j-1]; 47 dis[y][j]=dis[f[y][j-1]][j-1]+dis[y][j-1]; 48 } 49 } 50 } 51 } 52 } 53 void dfs(int x) 54 { 55 visit[x]=++tot;a[tot]=x; 56 for(int i=head[x];i;i=edge[i].next) 57 if(!visit[edge[i].to]) dfs(edge[i].to); 58 } 59 inline It L(It it) 60 { 61 if(it==s.begin()) return --s.end(); 62 return --it; 63 } 64 inline It R(It it) 65 { 66 if(it==--s.end()) return s.begin(); 67 return ++it; 68 } 69 ll LCA(int x,int y) 70 { 71 ll ans=0; 72 if(d[x]>d[y]) swap(x,y); 73 for(int i=t;i>=0;i--) 74 if(d[f[y][i]]>=d[x]) ans+=dis[y][i],y=f[y][i]; 75 if(x==y) return ans; 76 for(int i=t;i>=0;i--) 77 if(f[x][i]!=f[y][i]) ans+=dis[x][i]+dis[y][i],x=f[x][i],y=f[y][i]; 78 return ans+dis[x][0]+dis[y][0]; 79 } 80 int main() 81 { 82 scanf("%d%d",&n,&m);t=log2(n)+1; 83 for(int i=1;i<=n-1;i++) 84 { 85 int x=0,y=0; 86 ll z=0; 87 scanf("%d%d%lld",&x,&y,&z); 88 add(x,y,z); 89 add(y,x,z); 90 } 91 bfs(); 92 memset(visit,0,sizeof(visit)); tot=0; 93 dfs(1); 94 for(int i=1;i<=m;i++) 95 { 96 int x=0; 97 scanf("%d",&x); 98 if(!s.count(visit[x])) 99 { 100 if(s.size()) 101 { 102 it=s.lower_bound(visit[x]); 103 if(it==s.end()) it=s.begin(); 104 y=*L(it); 105 ans+=LCA(x,a[y])+LCA(x,a[*it])-LCA(a[y],a[*it]); 106 } 107 s.insert(visit[x]); 108 } 109 else 110 { 111 it=s.find(visit[x]); 112 y=*L(it),it=R(it); 113 ans-=LCA(x,a[y])+LCA(x,a[*it])-LCA(a[y],a[*it]); 114 s.erase(visit[x]); 115 } 116 printf("%lld\n",ans); 117 } 118 return 0; 119 }
这篇文章可以说是虎头蛇尾了!
end
*Update 2018929

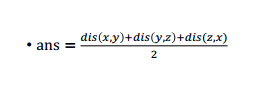


蓦然回首 那人已在灯火阑珊处.


