矩阵快速幂/矩阵加速线性数列 By cellur925

讲快速幂的时候就提到矩阵快速幂了啊，知道是个好东西，但是因为当时太蒟（现在依然）没听懂。现在把它补上。

一、矩阵快速幂

首先我们来说说矩阵。在计算机中，矩阵通常都是用二维数组来存的。矩阵加减法比较简单易懂，两个矩阵相加减就是两个行列数均相等的矩阵的对应位置的数相加减。

矩阵乘法就有些复杂了。它有一些特殊的要求，要求参与矩阵乘法运算的第一个矩阵的列数等于第二个矩阵的行数。所得的矩阵列数为第一个矩阵的列数，行数为第二个矩阵的行数。

举个栗子。

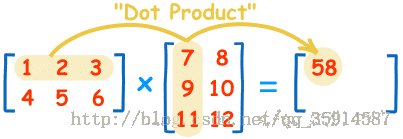
另外矩阵乘法有一些性质。满足结合律与分配律，不满足交换律（这很好理解）。

这是矩阵。

快速幂就比较显然了，我们先来复习一下快速幂的代码。

 1 long long poww(long long a,long long b)
 2 {
 3     long long ans=1;
 4     while(b>0)
 5     {
 6         if(b&1) ans=ans*a%k;
 7         b>>=1;
 8         a=a*a%k;
 9         
10     }
11     return ans;
12     
13 }
View Code

那么矩阵快速幂就不难理解了。设指数为k，我们可以用一个ans矩阵来代表最后结果，运行ksm函数。

ans的初值在ij相等时应为1.

个人习惯用结构体+二维数组存储矩阵。

(这里应该有代码）

至于模数，我们可以理性愉悦地运用膜的性质。

二、优化线性数列

这里省掉奇幻的引入用斐波那契栗子 喵~

我们直接看方法。

 

我们第一步需要构造基准矩阵，这也是最难的地方，想了好久才大概总结出一个方法。（还可能不对呢）

我们拿斐波那契数列来开刀：

f[i]=f[i-1]+f[i-2]

对于f[i]，找到最深需要追溯到的之前的值。在这里是f[i-2]。于是我们可以得到初始矩阵

-----------
| f[i-1]  |
|         |
| f[i-2]  |
|         |
|---------|

目标矩阵

------------
|   f[i]   |
|          |
|          |
|   f[i-1] |
|          |
-------------

（这里比较玄学 感性理解qwq）

-----------
| f[i-1]  |
|         |
| f[i-2]  |
-----------
　　　|
　　　|
　　　|

------------
|   f[i]   |
|          |
|          |
|   f[i-1] |
|          |
-------------




我们知道




f[i]=1*f[i-1]+1*f[i-2]
f[i-1]=1*f[i-1]+0*f[i-2]




于是取出他们的系数，得到




1    1

1    0




这里贴出LuoguP1939的代码






 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cstring>
 4 
 5 using namespace std;
 6 typedef long long ll;
 7 const ll moder=1e9+7;
 8 
 9 int T;
10 ll n;
11 struct matrix{
12     ll m[10][10];
13 }ans,sta;
14 
15 void init()
16 {
17     memset(ans.m,0,sizeof(ans.m));
18     for(int i=1;i<=3;i++) ans.m[i][i]=1;
19     memset(sta.m,0,sizeof(sta.m));
20     sta.m[1][1]=sta.m[1][3]=sta.m[2][1]=sta.m[3][2]=1;
21 }
22 
23 matrix mul(matrix a,matrix b)
24 {
25     matrix tmp;
26     memset(tmp.m,0,sizeof(tmp.m));
27     for(int i=1;i<=3;i++)
28         for(int j=1;j<=3;j++)
29             for(int k=1;k<=3;k++)    
30                 (tmp.m[i][j]+=(a.m[i][k]%moder)*(b.m[k][j]%moder))%=moder;
31     return tmp;
32 }
33 
34 void ksm(ll p)
35 {
36     while(p)
37     {
38         if(p&1) ans=mul(ans,sta);
39         p>>=1;
40         sta=mul(sta,sta);
41     } 
42 }
43 
44 int main()
45 {
46     scanf("%d",&T);
47     while(T--)
48     {
49         scanf("%lld",&n);    
50         if(n<=3){printf("1\n");continue;}
51         init();
52         ksm(n);
53         printf("%lld\n",ans.m[2][1]);
54     }
55     return 0;
56 }



View Code


未完待续







            

            
posted @ 
2018-08-23 16:47 
cellur925&Chemist 
阅读(298) 
评论(0) 
编辑 
收藏 
举报