51. N 皇后&52. N 皇后 II
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
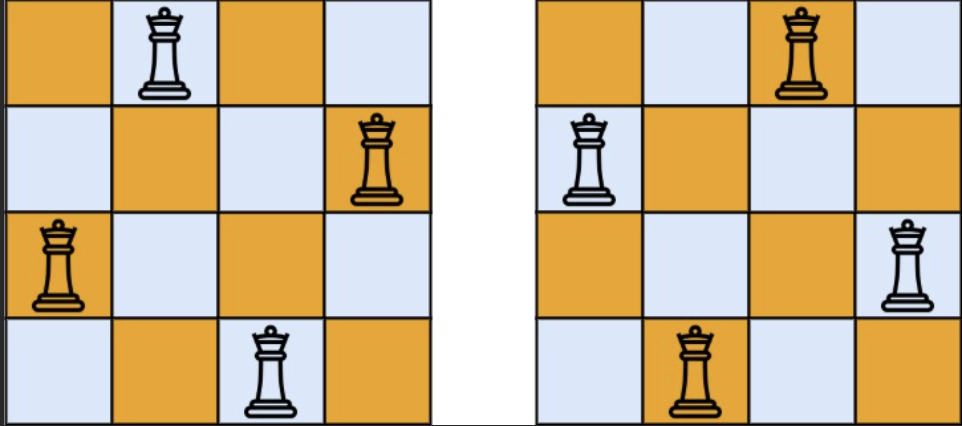
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/n-queens
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int isvalid(int *flag,int cur,int j){
int i;
for(i=0;i<cur;i++){
if(flag[i]==j||abs(flag[i]-j)==abs(i-cur)){
return 0;
}
}
return 1;
}
//cur为当前操作的行
void backtracking(int n,int cur,int *flag,char*** map,int* returnSize, int** returnColumnSizes){
int i,j;
if(cur==n){
map[*returnSize]=(char**)malloc(sizeof(char*)*n);
for(i=0;i<n;i++){
map[*returnSize][i]=(char*)malloc(sizeof(char)*(n+1));
for(j=0;j<n;j++){
if(flag[i]==j){
map[*returnSize][i][j]='Q';
}else{
map[*returnSize][i][j]='.';
}
}
map[*returnSize][i][j]='\0';
}//填充Q和‘.’
(*returnColumnSizes)[*returnSize]=n;
(*returnSize)++;
return;
}
for(j=0;j<n;j++){
if(isvalid(flag,cur,j)){ //这里判断为1时 执行isvalid判断为不可用,回溯执行backtracking
flag[cur]=j;
backtracking(n,cur+1,flag,map,returnSize,returnColumnSizes);
}
}
return;
}
char *** solveNQueens(int n, int* returnSize, int** returnColumnSizes){
int * flag=(int*)malloc(sizeof(int)*(n+1));
int i;
char ***map=(char***)malloc(sizeof(char**)*1000);
(*returnColumnSizes) = (int*)malloc(sizeof(int)*1000);
memset(flag,0,sizeof(flag));
*returnSize=0;
backtracking(n,0,flag,map,returnSize,returnColumnSizes);
return map;
}
延伸出的 n皇后 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
int totalNQueens(int n){
int * flag=(int*)malloc(sizeof(int)*(n+1));
int number=0;
memset(flag,0,sizeof(flag));
int *returnSize=(int*)malloc(sizeof(int));
*returnSize=0;
backtracking(n,0,flag,returnSize);
number=*returnSize;
return number;
修改最后返回的函数即完成(另外去除填充Q和'.'的部分)

