20230326

数据结构Remake第四天
🌲
隔壁拿来直接能跑的

#include <iostream>
using namespace std;

typedef struct Node
{//定义二叉树结构
    char data;
    struct Node *lchild,*rchild;
}*BiTree,BiTNode;

void CreateBiTree(BiTree &T)
{//先序创建二叉树
    char ch;
    cin>>ch;
    if(ch=='#') T=NULL;
    else{
        T=new BiTNode;
        T->data=ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}
void InOrderTraverse(BiTree T)
{//中序遍历
    if(T)
    {
        InOrderTraverse(T->lchild);
        cout<<T->data;
        InOrderTraverse(T->rchild);
    }
}
void PreOrderTraverse(BiTree T)
{//先序遍历
    if(T)
    {
        cout<<T->data;
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}
void PostOrderTraverse(BiTree T)
{//后序遍历
    if(T)
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        cout<<T->data;
    }
}
void Copy(BiTree T,BiTree &NewT)
{//二叉树的复制
    if(T==NULL){
        NewT=NULL;
        return;
    }else
    {
        NewT=new BiTNode;
        NewT->data=T->data;
        Copy(T->lchild,NewT->lchild);
        Copy(T->rchild,NewT->rchild);
    }
}
int Depth(BiTree T)
{//树的深度
    if(T==NULL)
        return 0;
    else
    {
        int m=Depth(T->lchild);
        int n=Depth(T->rchild);
        if(m>n) return (m+1);
        else return (n+1);
    }
}
int NodeCount(BiTree T)
{//统计二叉树中结点的个数
    if(T==NULL) return 0;
    else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}
int LeafCount(BiTree T)
{//统计二叉树中叶子结点的个数
    if(!T) return 0;
    if(!T->lchild &&!T->rchild){//如果二叉树左子树和右子树皆为空,说明该二叉树根节点为叶子节点,加1.
        return 1;
    }else{
        return LeafCount(T->lchild)+LeafCount(T->rchild);
    }
}
int Node_1_Count(BiTree T)
{//统计二叉树的度为1的结点个数
    if(!T) return 0;
    if((!T->lchild)&&(T->rchild)||(T->lchild)&&(!T->rchild))
        return 1 + Node_1_Count(T->lchild) + Node_1_Count(T->rchild);
    else
        return Node_1_Count(T->lchild) + Node_1_Count(T->rchild);
}
void PrintAllPath(BiTree T, char path[], int pathlen)
{//二叉树中从每个叶子结点到根结点的路径
  int i;
  if(T != NULL) {
    path[pathlen] = T->data; //将当前结点放入路径中
    if(T->lchild == NULL && T->rchild == NULL) {//叶子结点
        for(i = pathlen; i >= 0; i--)
            cout << path[i] << " " ;
      cout << endl;
    }else{
      PrintAllPath(T->lchild, path, pathlen + 1);
      PrintAllPath(T->rchild, path, pathlen + 1);
    }
  }
}
void ExChangeTree(BiTree &T)
{//构造函数，使用递归算法进行左右结点转换
    BiTree temp;
    if(T!=NULL){//判断T是否为空，非空进行转换，否则不转换
        temp=T->lchild;
        T->lchild=T->rchild;//直接交换节点地址
        T->rchild=temp;
        ExChangeTree(T->lchild);
        ExChangeTree(T->rchild);
    }
}
void DblOrderTraverse(BiTree T)
{//二叉树的双序遍历
    if(T)
    {
        cout<<T->data;
        DblOrderTraverse(T->lchild);
        cout<<T->data;//访问两遍
        DblOrderTraverse(T->rchild);
    }
}
int main()
{
    BiTree T;
    //测试例子AB#CD##E##F#GH###
    cout<<"先序遍历输入(以#结束):";
    CreateBiTree(T);
    cout<<"中序遍历输出:";
    InOrderTraverse(T);
    cout<<endl<<"先序遍历输出:";
    PreOrderTraverse(T);
    cout<<endl<<"后序遍历输出:";
    PostOrderTraverse(T);
    cout<<endl<<"树的深度:"<<Depth(T);
    cout<<endl<<"结点的个数:"<<NodeCount(T);
    cout<<endl<<"叶结点的个数:"<<LeafCount(T);
    cout<<endl<<"度为1的结点个数:"<<Node_1_Count(T);
    cout<<endl<<"二叉树中从每个叶子结点到根结点的所有路径："<<endl;
    char path[256];
    int pathlen=0;
    PrintAllPath(T,path,pathlen);//
    //交换二叉树每个结点的左孩子和右孩子
    BiTree tem=T;//直接复制一颗树，在不改变原树的前提下，对临时树进行交换。
    ExChangeTree(tem);
    cout<<"先序遍历输出交换后的结果:";
    PreOrderTraverse(tem);
    cout<<endl<<"双序遍历输出:";
    DblOrderTraverse(T);
    printf("\n");
    return 0;
}

运行结果为

先序遍历输入(以#结束):AB#CD##E##F#GH###
中序遍历输出:BDCEAFHG
先序遍历输出:ABCDEFGH
后序遍历输出:DECBHGFA
树的深度:4
结点的个数:8
叶结点的个数:3
度为1的结点个数:3
二叉树中从每个叶子结点到根结点的所有路径：
D C B A 
E C B A 
H G F A 
先序遍历输出交换后的结果:AFGHBCED
双序遍历输出:AFGGHHFABCEECDDB

1|0中序遍历算法

void InOrderTraverse(BiTree T)
{//中序遍历
    if(T)
    {
        InOrderTraverse(T->lchild);
        cout<<T->data;
        InOrderTraverse(T->rchild);
    }
}

其中中序遍历还比较模糊，所以画了个图再推了一遍

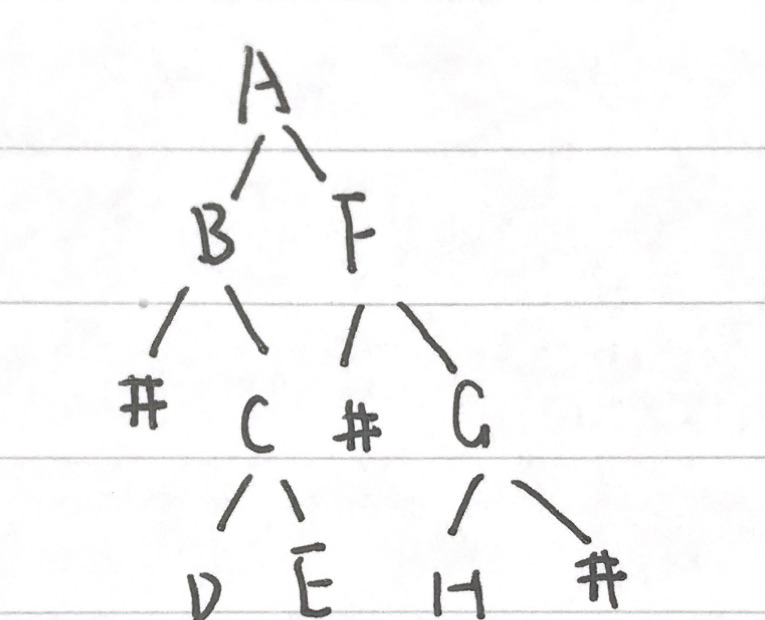
第一次推的结果是DCEBAHGF
但是中序遍历先访问左子树，再访问根节点，即左节点为空直接访问根节点再访问右节点
所以结果应该是BDCEAFHG

__EOF__

本文作者：noobwei
本文链接：https://www.cnblogs.com/noobwei/p/17258976.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！