欧拉函数φ(x)简要介绍及c++实现
我还是很喜欢数论,从此吃喝不问,就此沉沦。
欧拉函数φ(x)的值为在[1,x)的区间内与x互质的数的个数
通式: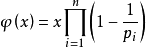 其中p1, p2……pn为x的所有质因数,x是不为0的整数。φ(1)=1。
其中p1, p2……pn为x的所有质因数,x是不为0的整数。φ(1)=1。
注意:每种质因数只一个。 比如12=2*2*3那么φ(12)=12*(1-1/2)*(1-1/3)=4
介绍几个性质:
1.若n是质数p的k次幂,则 ,因为除了p的倍数外,其他数都跟n互质。
,因为除了p的倍数外,其他数都跟n互质。
2.积性函数——若m,n互质,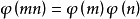 。
。
3.当n为质数时,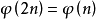 , 其实与上述类似。
, 其实与上述类似。
4.若n为质数则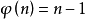 , 这个挺重要的。
, 这个挺重要的。
5.一个数的所有质因子之和是φ(n)*n/2。

1 //用通式算的 2 int euler(int n){ //返回euler(n) 3 int res=n,a=n; 4 for(int i=2;i*i<=a;i++){ 5 if(a%i==0){ 6 res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出 7 while(a%i==0) a/=i; 8 } 9 } 10 if(a>1) res=res/a*(a-1); 11 return res; 12 }

1 //筛选法打欧拉函数表 2 #define Max 1000001 3 int euler[Max]; 4 void Init(){ 5 euler[1]=1; 6 for(int i=2;i<Max;i++) 7 euler[i]=i; 8 for(int i=2;i<Max;i++) 9 if(euler[i]==i) 10 for(int j=i;j<Max;j+=i) 11 euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出 12 } 13 */
Stay Hungry, Stay Foolish



 浙公网安备 33010602011771号
浙公网安备 33010602011771号