数据结构-树

判断题

1.'关于树和二叉树

二叉树是度为 2 的树。

     T      F

2.具有10个叶结点的二叉树中，有9个度为2的结点。

     T      F

3.某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无左孩子。

     T      F

4.若一个结点是某二叉树的中序遍历序列的最后一个结点，则它必是该树的前序遍历序列中的最后一个结点。

     T      F

5.某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无右孩子。

     T      F

6.若A和B都是一棵二叉树的叶子结点，则存在这样的二叉树，其前序遍历序列为...A...B...，而中序遍历序列为...B...A...。

     T      F

先序中序后序是对根结点而言的，叶子结点的顺序保持不变。

7.二叉树的前序遍历并不能唯一确定这棵树，但是如果我们还知道该树的根结点是那一个，则可以确定这棵二叉树（ ）。

     T      F

8.将一棵完全二叉树存于数组中（根结点的下标为1）。则下标为23和24的两个结点是兄弟。

     T      F

选择题

1.设树T的度为4，其中度为1、2、3、4的结点个数分别为4、2、1、1。则T中有多少个叶子结点？

    A.4
    B.6
    C.8
    D.10

结点个数和度数满足下面的公式:

\[\color{red}{\sum\limits_{i=1}^{n}Degree(i)+1=n} \]

2.设每个d叉树的结点有d个指针指向子树，有n个结点的d叉树有多少空链域？

    A.nd
    B.n(d−1)
    C.n(d−1)+1
    D.以上都不是

3.已知一棵二叉树的先序遍历结果是ABC，则以下哪个序列是不可能的中序遍历结果：

    A.ABC
    B.BAC
    C.CBA
    D.CAB

叶子结点的相对顺序不能变，A肯定是根结点，C一定是叶子结点，B不一定，可以排除A、B，中序CAB说明B和C都是叶子结点，所以错。

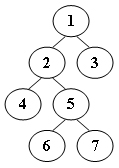
4.给定二叉树如下图所示。设N代表二叉树的根，L代表根结点的左子树，R代表根结点的右子树。若遍历后的结点序列为3、1、7、5、6、2、4，则其遍历方式是：

    A.NRL
    B.RNL
    C.LRN
    D.RLN

5.设高为h的二叉树（规定叶子结点的高度为1）只有度为0和2的结点，则此类二叉树的最少结点数和最多结点数分别为：

    A.2h, 2^h−1
    B.2h−1, 2^h−1
    C.2h−1, 2^h-1−1
    D.2^h-1+1, 2^h−1

最少的情况为除了第一层，其他层结点个数为0；最多的情况是满二叉树。

6.在下述结论中，正确的是：

①只有一个结点的二叉树的度为0;

②二叉树的度为2；

③二叉树的左右子树可任意交换；

④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。

    A.①④
    B.②④
    C.①②③
    D.②③④

7.任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序

    A.发生改变
    B.不发生改变
    C.不能确定
    D.以上都不对

8.如果二叉树的前序遍历结果是12345，后序遍历结果是32541，那么该二叉树的中序遍历结果是什么？

    A.23145
    B.23154
    C.24135
    D.无法确定

能确定2和4一定是1的子节点，但无法确定3和5，先序和后序不能确定树。

9.要使一棵非空二叉树的先序序列与中序序列相同，其所有非叶结点须满足的条件是：

    A.只有左子树
    B.只有右子树
    C.结点的度均为1
    D.结点的度均为2

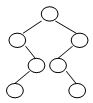
10.已知一棵二叉树的树形如下图所示，其后序序列为{ e, a, c, b, d, g, f }。树中与结点a同层的结点是：

    A.c
    B.d
    C.f
    D.g

11.如果二叉树的后序遍历结果是FDEBGCA，中序遍历结果是FDBEACG，那么该二叉树的前序遍历结果是什么？

    A.ABCDEFG
    B.ABDFEGC
    C.ABDFECG
    D.ABDEFCG

12.已知二叉树的后序遍历是dabec，中序遍历是debac，则其前序遍历是（）。

    A.acbed
    B.decab
    C.deabc
    D.cedba

13.某二叉树的先序序列和后序序列正好相反，则下列说法错误的是（）。

    A.二叉树不存在
    B.若二叉树不为空，则二叉树的深度等于结点数
    C.若二叉树不为空，则任一结点不能同时拥有左孩子和 右孩子
    D.若二叉树不为空，则任一结点的度均为1

14.对二叉树的结点从1开始进行编号，要求每个结点的编号大于其左右孩子的编号，同一结点的左右孩子中，其左孩子的编号小于其右孩子的编号，可采用（）遍历实现编号。

    A.中序
    B.后序
    C.层序
    D.先序

15.在一非空二叉树的中序遍历中，根结点的右边（）。

    A.只有右子树上的所有结点
    B.只有右子树上的部分结点
    C.只有左子树上的部分结点
    D.只有左子树上的全部结点

16.一棵树可转换成为与其对应的二叉树，则下面叙述正确的是（）。

    A.树的先根遍历序列与其对应的二叉树的先序 遍历相同
    B.树的后根遍历序列与其对应的二叉树的后序遍历相同
    C.树的先根遍历序列与其对应的二叉树的中序遍历相同
    D.以上都不对

将树转换成与其对应的二叉树，将结点的孩子放在左子树；将结点的兄弟放在右子树。

17.已知一棵二叉树的先序序列和中序序列分别为GFDBHCEA和DFHBGCAE，则该二叉树的后序序列为（）。

    A.DHBFAECG
    B.DHBFEACG
    C.DBHFAECG
    D.DFAEHBCG

18.设x和y是二叉树中的任意两个结点，若在先序遍历中x在y之前，而在后序遍历中x在y之后，则x和y的关系是（）。

    A.x是y的左兄弟
    B.x是y的右兄弟
    C.x是y的祖先
    D.x是y的子孙

19.以下算法的功能是（）。

int function(BTreeNode* BT, ElemType x){
   int n=0;
   if(BT!=NULL)
   {   
        if(BT->data==x)   n++;
        n+= function (BT->left, x);
        n+= function (BT->right, x);
}
   return n;
}

    A.求二叉树结点个数
    B.求二叉树中值为x的结点个数
    C.求二叉树中值为x结点为根的子树结点数
    D.求二叉树左右子树结点数

20.以下算法的功能是（）。

void test(bitree *t)
{
   if (t) 
   {
      test(t->lchild);
      test(t->rchild);
      cout<<t->data;
   }
}

    A.输出二叉树的根结点值
    B.前序遍历二叉树
    C.中序遍历二叉树
    D.后序遍历二叉树

21.一棵有1025个结点的二叉树的高度为多少?

    A.10
    B.11
    C.11～1025之间
    D.10～1024之间

小心不一定是完全二叉树

22.一棵度为4的树中有20个度为4的结点、10个度为3的结点、1个度为2的结点和10个度为1的结点, 则叶子结点有多少个?

    A.41
    B.82
    C.113
    D.122

程序填空题

下列代码的功能是将二叉树T中的结点按照层序遍历的顺序输出。

typedef struct TreeNode *Tree;
struct TreeNode
{
    int Key;
    Tree Left;
    Tree Right;
};

void Level_order ( Tree T )
{
    Queue Q;
    if ( !T ) return;
    Q = CreateQueue( MaxElements );
    Enqueue( T, Q );
    while ( !IsEmpty( Q ) ){
        T = Front_Dequeue ( Q ); /* return the front element and delete it from Q */
        printf("%d ", T->Key);
        if ( T->Left )
            (3分);
        if ( (3分) )
            (3分);
    }
}