hdu6775 Fibonacci Sum(裴波纳妾通项公式+二项式定理展开+等比数列求和)

题目
求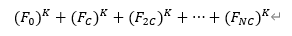，mod1e9+9.
解法：首先要知道通项公式且能将其转化为mod意义下整数（解二次同余方程）。
将每一项展开，观察到纵向为一个n+1项的等比数列，等比数列求和可以有优化掉些快速幂，

#include<bits/stdc++.h>
typedef  long long ll ;
#define mod 1000000009
#define gcd __gcd
#define rep(i , j , n) for(int i = j ; i <= n ; i++)
#define red(i , n , j)  for(int i = n ; i >= j ; i--)
#define ME(x , y) memset(x , y , sizeof(x))
#define INF  0x3f3f3f3f
#define PI acos(-1)
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define all(v) v.begin(),v.end()
#define size(v) (int)(v.size())
#define lson l,mid,root<<1
#define rson mid+1,r,root<<1|1
#define int ll
using namespace std;
const int N = 1e6+9;
const int maxn = 1e5+9;
const int esp = 1e-4;
int fac[maxn] , inv[maxn];
int A = 691504013 , B = 308495997 , C = 276601605 , AA = 691504012;
//Fn ≡ 276601605（691504013^n - 308495997^n）(mod (1e9+9))
int quickpow(int a , int b){
    int ans = 1 ;
    while(b){
        if(b&1){
            ans = ans * a % mod ;
        }
        b >>= 1 ;
        a = a * a % mod;
    }
    return ans ;
}

void init(){
    fac[0] = inv[0] = 1 ;
    rep(i , 1 , maxn-9){
        fac[i] = fac[i-1] * i % mod;
    }
    inv[maxn-9] = quickpow(fac[maxn-9] , mod-2);
    red(i , maxn-10 , 1){
        inv[i] = inv[i+1] * (i + 1) % mod ;
    }
}

int Cn(int n , int k){
    return fac[n] * inv[k] % mod * inv[n-k] % mod ;
}

void solve(){
    int ans = 0 ;
    int n , c , k;
    scanf("%lld%lld%lld" , &n , &c , &k);
    int nn = n%(mod-1) , cc = c%(mod-1);
    int DD = quickpow(AA*B%mod , c);//二项式递推
    int q = quickpow(quickpow(A , c) , k);//公比
    int n1 = (n+1)%mod;//(n+1)项
    int n2 = (n+1)%(mod-1);//降幂
    int Q = quickpow(q , n2);//an项
    int D = quickpow(DD , n2);//an项递推
    rep(i , 0 , k){
        int cur = Cn(k , i);//组合数
        if(i&1) cur = mod - cur ;
        if(q == 1) ans = (ans + cur * n1%mod) % mod ;//公比为1
        else{
            ans = (ans + cur*(Q+mod-1)%mod * quickpow(q-1 , mod-2)%mod)%mod;//首项为1的等比数列求和
        }
        q = q * DD % mod ;//公比递推
        Q = Q * D % mod ;//an项递推
    }
    cout << ans * quickpow(C , k) % mod << endl;
}

signed main()
{
/*#ifdef ONLINE_JUDGE
#else
    freopen("D:\\c++\\in.txt", "r", stdin);
#endif*/
    init();
    int t ;
    scanf("%lld" , &t);
    while(t--)
        solve();

}