Codeforces Round #652 (Div. 2)A、B、C、D

题目
A题意：给出一个n条边的正多边形可以任意旋转，问能否使至少一边平行x轴，一条边平行y轴。
解法：该图形得关于x轴和y轴对称能像正方形一样被4等分，所以是4得倍数。

void solve(){
    int n ;
    cin >> n ;
    if(n%4==0){
        cout << "YES" << endl;
    }else{
        cout << "NO" << endl;
    }
}

B题意：给出一个01字符串，操作：如果存在两个字符\(s_i = 1 , s_{i+1} = 0\)可以选择任意一个删除。经过操作后，输出字典序最小得字符串。
解法：找到第一个1，最后一个0，这之间得字符串除最后一个零都可以删除，如果没找到则原串输出。

const int maxn = 1e5+9;
char s[maxn];
void solve(){
    int n ;
    cin >> n ;
    scanf("%s" , s+1);
    int index = -1;
    red(i , n , 1){
        if(s[i] == '0'){
            index = i ;
            break;
        }
    }
    int index2 = -1 ;
    rep(i , 1 , index-1){
        if(s[i] == '1'){
            index2 = i ;
            break;
        }
    }
    if(index != -1 && index2 != -1){
        rep(i , 1 , n){
            if(i >= index2 && i < index){
                continue;
            }else{
                cout << s[i] ;
            }
        }
        cout << endl;
    }else{
        printf("%s" , s+1);
        cout << endl;
    }
}

C题意：给出n个数ai，k个人每个分配wi给数，定义每个人得和为该人获得得最大值加最小值之和，问所以人之和最大为多少。
解法：排序，贪心。

const int maxn = 2e5+9;
vector<int>v[maxn];
void solve(){
    int n , k ;
    cin >> n >> k ;
    rep(i , 0 , n) v[i].clear();
    vector<int>a(n) , w(k);
    rep(i , 0 , n-1){
        cin >> a[i];
    }
    rep(i , 0 , k-1){
        cin >> w[i];
    }
    sort(all(a));
    sort(all(w));
    reverse(all(a));
    rep(i , 0 , k-1){//按w从小到大分配，依次从大到小分配a给每个人
        v[i].pb(a[i]);
        w[i]--;
    }
    int j = k ;//前k个数已经分配完毕，从第k大一直到最小值
    rep(i , 0 , k-1){同样按w从小到大分配
        while(w[i]){
            v[i].pb(a[j]);
            j++;
            w[i]--;
        }
    }
    int ans = 0 ;
    rep(i , 0 , k-1){
        ans += v[i][0] + v[i][size(v[i])-1] ;//最大加最小
    }
    cout << ans << endl;
}

D题意：最初有一个结点，衍生规则如下：

• 如果结点 u 没有子结点，添加 1 个子结点
• 如果结点 u 有 1 个子结点，添加 2 个子结点
• 如果结点 u 有 3 个子结点，跳过该结点
  如
  
  

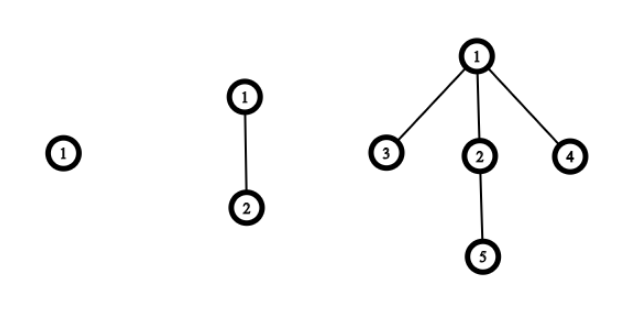
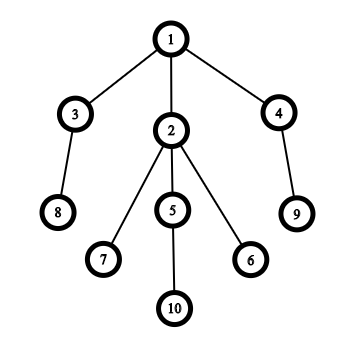
爪形结构如下：

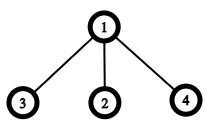
问可以在 \(level_n\) 选出几个互不相交的爪形结构。
解法：根据前前四个level，可以发现有\(level_i由两个level_{i-2}、一个level_{i-1}和一个根节点构成\)。
所以有递推式：\(dp[i] = 2*dp[i-2] + dp[i-1] + (i\%3==0)\),当i是3得倍数时，根节点可以作为1个爪形且不影响其子树得爪形。

const int maxn = 2e6+9;
int n , k ;
int dp[maxn];
void init(){
    dp[1] = dp[2] = 0 ;
    dp[3] = dp[4] = 1 ;
    rep(i , 5 , 2e6){
        dp[i] = (2*dp[i-2] + dp[i-1] + (i%3==0))%mod;
    }
}
void solve(){
    int n ;
    cin >> n ;
    cout << 4*dp[n]%mod << endl;
}