GarsiaWachs算法
这个算法可以用来解决石子合并问题(大数据版）。
洛谷有题：P5569 [SDOI2008]石子合并
对于一堆石子（链式）：
1. 从最左边开始向右走直到 stone[ k ] <= stone[ k + 2 ] 然后合并 stone[ k + 1 ] += stone[ k ]；
2. 从k 往前走 直到 stone[ j ] > stone[ k ] + stone[ k + 1 ] 然后将新合并的数放在 j 后面
如果不存在这样的 j ，就放在最前面
3. 如果我们找不到这样的 k , 就合并最后的两个数即 stone[ n ] 和 stone[ n - 1 ] （显然这两个数是最小的)
4. 重复第一步。
代码如下：
1 /* 2 2019-10-30 3 P5569 [SDOI2008]石子合并 4 czq 5 */ 6 7 #include <cstdio> 8 #include <iostream> 9 #include <algorithm> 10 using namespace std; 11 const int N = 4e4 + 10; 12 13 int n; 14 int stone[N]; 15 16 int main() 17 { 18 cin >> n; 19 for(int i = 1; i <= n; i++) scanf("%d", &stone[i]); 20 21 //left 代表最左边的下标， ans 记录答案 22 int ans = 0, left = 1; 23 24 //当至少存在三堆石子时， 即 left n-1 n 25 while(left < n - 1) 26 { 27 int k; 28 for(k = left; k < n - 1; k++) 29 { 30 if(stone[k] <= stone[k+2]) 31 { 32 stone[k+1] += stone[k]; //合并 33 ans += stone[k+1]; //加到答案里 34 // k 左边的往右移一位 将 k 覆盖掉 35 for(int j = k; j > left; j--) stone[j] = stone[j - 1]; 36 left ++; //由于移位所以最左边要加 1 37 38 //向左查找 也就是第二步 39 int j = k + 1; 40 while(stone[j] > stone[j-1] && j > left) 41 { 42 //交换，将新合并石子的前移 43 swap(stone[j], stone[j-1]); 44 j --; 45 } 46 break; 47 } 48 } 49 //不存在这样的 k 50 if(k == n - 1) 51 { 52 //将最右边的石子加到倒数第二堆， 53 stone[n - 1] += stone[n]; 54 //加上目前最右边的石子, 最右边的石子已经不存在了 所以 --n 55 ans += stone[--n]; 56 } 57 } 58 59 //加上还剩下的两堆石子 60 ans += stone[n] + stone[n-1]; 61 62 cout << ans << endl; 63 64 return 0; 65 }
如果看不懂代码看例子
接下来举个例子：假设有 6 堆石子： left = 1 n = 6 ans = 0 d 为新合并的数
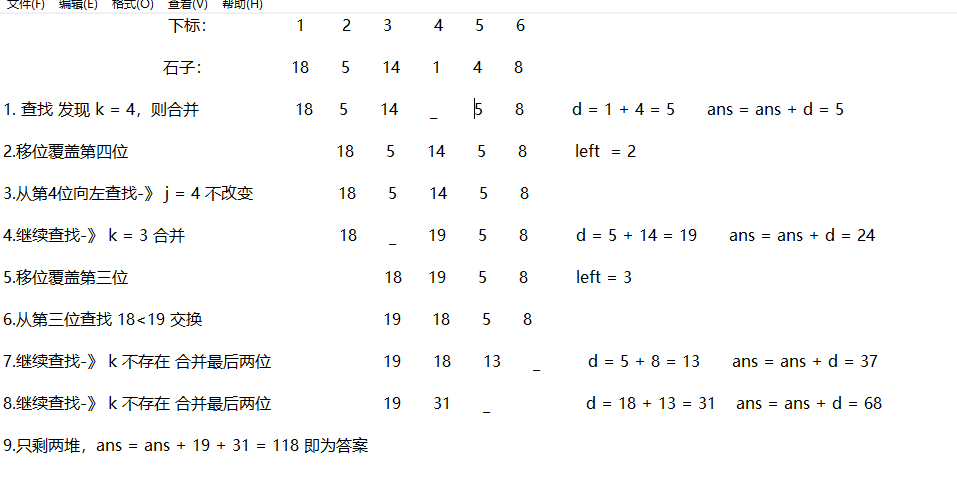
代码运行截图：
随机举的例子，不是很好，可以自己在理解一下
