推荐系统实践 0x0e LS-PLM
在之前介绍的几个模型中,存在这些问题:
- LR不能捕捉非线性,只能进行一次的回归预测
- GBDT+LR虽然能够产生非线性特征组合,但是树模型不适用于超高维稀疏数据
- FM利用二阶信息来产生变量之间的相关性,但是无法适应高阶组合特征,高阶组合容易爆炸
那么,下面介绍的LS-PLM模型一定程度上缓解了这个问题。
LS-PLM
LS-PLM是阿里巴巴曾经主流的推荐模型,这一篇文章就来介绍一下LS-PLM模型的内容。LS-PLM可以看做是对LR模型的自然推广,它采用的是分而治之的策略。先对样本分片,然后样本分片中运用逻辑回归进行预估。分片的作用是为了能够让CTR模型对不同的用户群体。不同使用场景都具有针对性。先对全量样本进行聚类,然后在对每个分类实施逻辑回归。透漏一下,这里阿里巴巴使用的分片聚类的经验值是12。
论文当中LS-PLM的效果与LR模型效果进行对比,如下图所示。
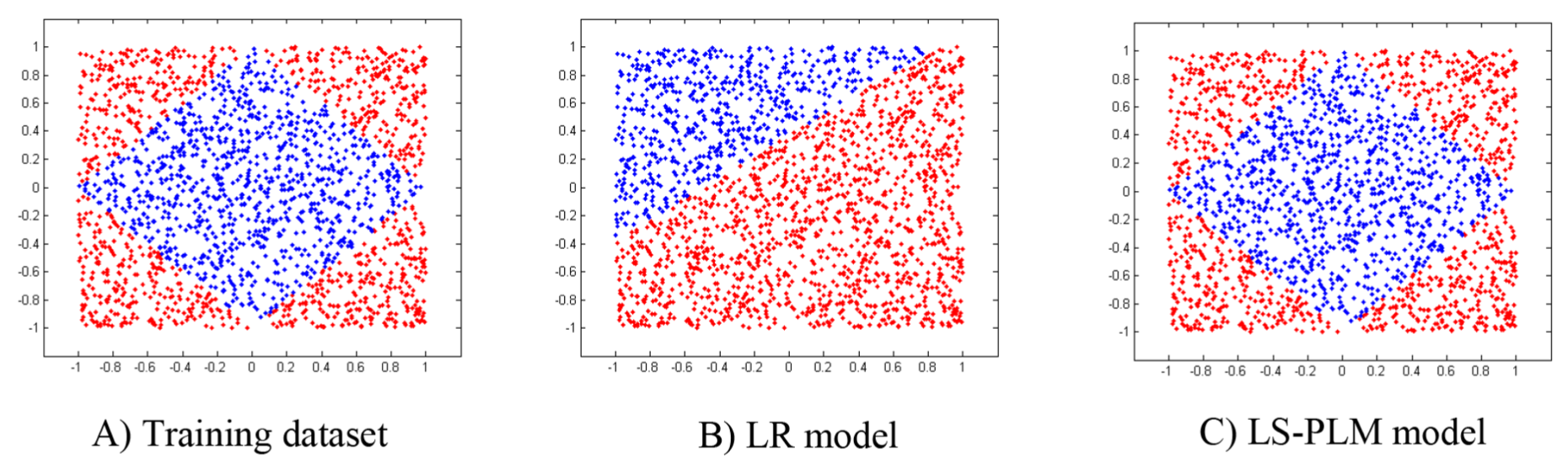
优势
LS-PLM存在三个优势:
- 端到端的非线性学习能力。通过足够的划分区域,LS-PLM可以拟合任何复杂的非线性函数,挖掘数据中的非线性模式,节省大量人工处理样本和特征工程的过程。
- 可扩展性。与LR模型类似,LS-PLM可以扩展到大量样本和高维特征。在这之上设计了一个分布式系统,可以在数百台机器上并行训练模型。在线产品系统中,每天都会训练和部署几十个具有数千万参数的LS-PLM模型。
- 稀疏性。模型稀疏性是工业环境下在线服务的一个实际问题。这里展示了采用L1和L2,1正则器的LS-PLM可以实现良好的稀疏性。使得部署更加轻量级,在线推断效率也更高。
论文基于directional derivatives(方向导数)和quasi-Newton(拟牛顿)方法来解决因为正则项使得目标函数非凸的问题。
数学形式
LS-PLM的数学形式如下面公式所示
首先用聚类函数\(\pi\)对模型进行分类分片,再用LR模型计算样本在分片中具体的CTR,然后将两者相乘之后求和。公式中的\(m\)就是分片数,可以较好地平衡模型的拟合能力和推广能力。当\(m=1\)时就会退化为普通的逻辑回归。
实际上,LS-PLM采用的softma函数x进行分类,sigmoid函数作为回归。于是公式变成:
\(\{u_1,...u_m\}\)为聚类函数(分片函数)\(\pi_i\)的参数,\(\{w_1,...w_m\}\)为拟合函数\(\eta_i\)的参数。
优化
由于目标函数中的加入的正则化项\(L_1\),\(L_{2,1}\)都是非平滑函数,所以目标函数也是非平滑的、非凸函数。因为目标函数的负梯度方向并不存在,所以用能够得到f最小的方向导数的方向b作为负梯度的近似值。这里的推导比较复杂,可以看一下原来论文,之后我尽可能用通俗易懂的语言补充这里。
这个\(L_{2,1}\)挺意思的,贴一下它原来的公式:
代码
import torch
import torch.nn as nn
import torch.optim as optim
class LSPLM(nn.Module):
def __init__(self, m, optimizer, penalty='l2', batch_size=32, epoch=100, learning_rate=0.1, verbose=False):
super(LSPLM, self).__init__()
self.m = m
self.optimizer = optimizer
self.batch_size = batch_size
self.epoch = epoch
self.verbose = verbose
self.learning_rate = learning_rate
self.penalty = penalty
self.softmax = None
self.logistic = None
self.loss_fn = nn.BCELoss(reduction='mean')
def fit(self, X, y):
if self.softmax is None and self.logistic is None:
self.softmax = nn.Sequential(
nn.Linear(X.shape[1], self.m).double(),
nn.Softmax(dim=1).double()
)
self.logistic = nn.Sequential(
nn.Linear(X.shape[1], self.m, bias=True).double()
, nn.Sigmoid())
if self.optimizer == 'Adam':
self.optimizer = optim.Adam(self.parameters(), lr=self.learning_rate)
elif self.optimizer == 'SGD':
self.optimizer = optim.SGD(self.parameters(), lr=self.learning_rate, weight_decay=1e-5, momentum=0.1,
nesterov=True)
# noinspection DuplicatedCode
for epoch in range(self.epoch):
start = 0
end = start + self.batch_size
while start < X.shape[0]:
if end >= X.shape[0]:
end = X.shape[0]
X_batch = torch.from_numpy(X[start:end, :])
y_batch = torch.from_numpy(y[start:end]).reshape(1, end - start)
y_batch_pred = self.forward(X_batch).reshape(1, end - start)
loss = self.loss_fn(y_batch_pred, y_batch)
loss.backward()
self.optimizer.step()
start = end
end += self.batch_size
if self.verbose and epoch % (self.epoch / 20) == 0:
print('EPOCH: %d, loss: %f' % (epoch, loss))
return self
def forward(self, X):
logistic_out = self.logistic(X)
softmax_out = self.softmax(X)
combine_out = logistic_out.mul(softmax_out)
return combine_out.sum(1)
def predict_proba(self, X):
X = torch.from_numpy(X)
return self.forward(X)
def predict(self, X):
X = torch.from_numpy(X)
out = self.forward(X)
out[out >= 0.5] = 1.0
out[out < 0.5] = 0.0
return out
参考
深度学习推荐系统 王喆编著
Learning Piece-wise Linear Models from Large Scale Data for Ad Click Predict
Github:hailingu/MLFM
LS-PLM学习笔记
文章转载请注明出处,喜欢文章的话请我喝一杯咖啡吧!在右边赞助里面哦!谢谢! NoMornings.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号