论文出自:Shazeer N, Mirhoseini A, Maziarz K, et al. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer[J]. arXiv preprint arXiv:1701.06538, 2017.
摘要
- 神经网络的吸收信息的容量(capacity)受限于参数数目。
- 条件计算(conditional computation)针对于每个样本,激活网络的部分子网络进行计算,它在理论上已证明,可以作为一种显著增加模型容量的方法。
- 在实际中,我们在牺牲少量计算效率的情况下,实现了 1000 倍的模型容量(model capacity)的提升。
- 我们引入了稀疏门控专家混合层(Sparsely-Gated Mixture-of-Experts Layer),包括数以千计的前馈子网络。对于每一个样本,有一个可训练的门控网络(gating network)会计算这些专家(指前馈子网络)的稀疏组合。
- 我们把专家混合(MoE)应用于语言建模和机器翻译任务中,对于这些任务,从训练语料库中吸收的巨量知识,是十分关键的。
- 在我们提出的模型架构里,MoE 包含 1370 亿个参数,以卷积的方式放在堆叠 LSTM 层之间。
- 在大型语言建模和及其翻译的基准测试中,该模型以更少的计算成本,实现了比最先进方法更好的结果。
1 介绍和相关工作
1.1 条件计算
- 充分利用训练数据和模型大小的规模,一直以来都是深度学习成功的关键。
- 当训练集足够大,增加神经网络的容量(即参数数目),可以得到更高的预测准确度。
- 对于传统的深度学习模型,对每一个样本都会激活整个模型,这会导致在训练成本上,以大约二次方的速度增长,因为模型大小和训练样本数目都增加了。
- 当前计算能力和分布式计算的进展,并不能满足这样的需求。
- 因此有很多工作提出了各种形式的条件计算,它们在不显著增加计算成本的情况下,尽量增加模型的容量。
- 在这些算法里,以每个样本为基础(on a per-example basis),会激活或冻结网络中的大部分。
- 这种门控决策机制,可以是二进制的,也可以是稀疏而连续的;可以是随机性的,也可以是确定性的。
- 门控决策通过有各种形式的强化学习和反向传播来训练。
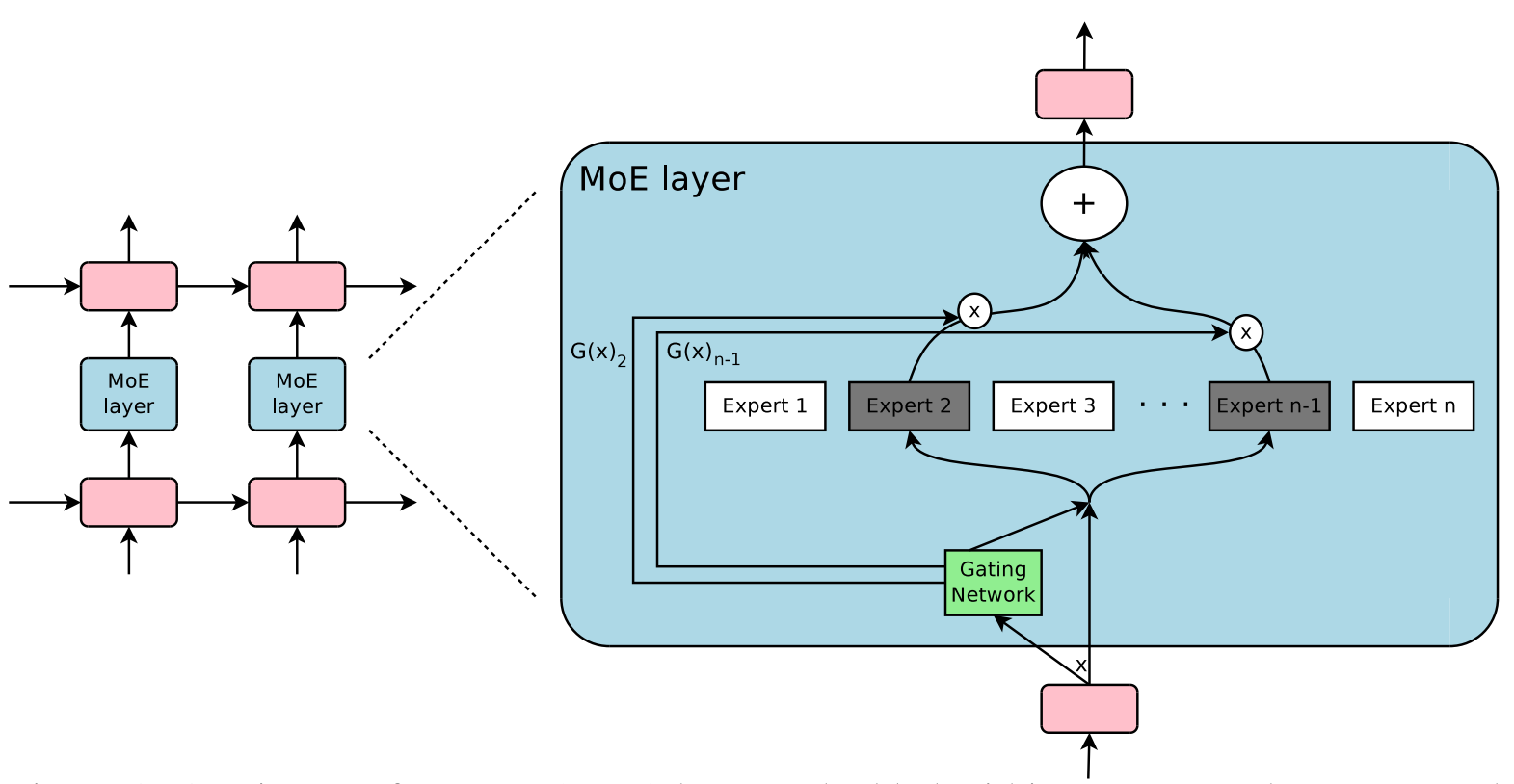
Figure 1:MoE 层嵌入到循环语言模型中。在本例中,稀疏的门控函数选择两个专家来执行计算。门控网络会调整专家的输出。
- 尽管这种思想在理论上很有前景,但是目前为止,还没有工作展现在模型容量、训练时间或模型质量上有足够的提升。我们把原因归结为这些挑战:
- 现代计算设备(特别是 GPU),相比分支(branching)而言,在数值计算上更快。
- 大的批量大小对于性能很关键。而条件计算减少了批量大小。
- 网络带宽会成为性能瓶颈。
- 损失项可能对于实现好的效果是必需的,因此损失项可能会影响模型质量和负载平衡。
- 对于大型数据集,模型容量是最关键的。目前条件计算的文献处理的图像识别数据集都相对太小了,难以为大模型提供足够多的信号。
- 本文首先解决了上述挑战,并且最后看到了条件计算的前景。
- 我们得到了 1000 倍的模型容量提升,只花费了少量计算开销
- 得到的结果也优于最顶尖的结果
1.2 本文方法:稀疏门控专家混合层
- 我们的条件计算方法,就是引入了一个新的通用神经网络组件类型:稀疏门控专家混合层。
- MoE 包含:
- 一些专家,每个专家都是一个简单的前馈神经网络。
- 一个可训练的门控网络,它会挑选专家的一个稀疏组合,用来处理每个输入。
- 所有网络都是使用反向传播联合训练的。
- 尽管该技术是通用的,但是本文聚焦在语言建模和机器翻译任务中(这些任务都受益于非常大的模型)。
- 具体说来,如图一所示,我们把 MoE 以卷积的方式(convolutionally)放在多层 LSTM 层之间。
- 在文本的每个位置上,就会调用 MoE 一次,进而可能选择不同的专家组合。
- 不同的专家会倾向于变得高度专业化(基于语法和语义)。
1.3 专家混合的相关工作
2 混合专家层的结构
MoE 层包括 :
- $n$ 个“专家网络”:$E_{1}, \cdots, E_{n}$。
- 一个门控网络 $G$,其输出是一个稀疏的 $n$ 维向量。
尽管从理论上讲,每个专家网络只要保持一致的输入大小和输出大小就可以了;但是,在本文的研究里,我们限制了专家网络具有相同的网络结构,而网络参数保持独立。
给定输入 $x$,定义 $G(x)$ 是门控网络的输出;$E_{i}(x)$ 是第 $i$ 个专家网络的输出。于是 MoE 模块的输出为:
\begin{equation}
y=\sum_{i=1}^{n} G(x)_{i} E_{i}(x)
\end{equation}
基于 $G(x)$ 输出的稀疏性,我们可以节省计算量。
- 当 $G(x)_{i}=0$ 时,我们无需计算 $E_{i}(x)$。
- 在我们的实验中,我们有数以千计的专家,但是针对每个样本,只需要用到少量的专家。
- 如果专家数目非常大,我们可能要采用层次化的 MoE;本文我们不会使用层次化的 MoE,相关细节感兴趣可以见附录 B。
2.1 门控网络
Softmax Gating
一种朴素的想法是,用一个矩阵乘上输入,然后经过一个 Softmax 函数,这种方法实际上是一种非稀疏的门控函数:
\begin{equation}
G_{\sigma}(x)=\operatorname{Softmax}\left(x \cdot W_{g}\right)
\end{equation}
Noise Top-K Gating
我们在 Softmax 门控网络基础上,加入两个元素:稀疏性和噪声。在执行 Softmax 函数之前:
- 我们加入了可调的高斯噪声
- 噪声项是为了帮助负载均衡(load balancing),我们在附录 A 有详细讨论。
- 并且保留前 k 个值
- 这种稀疏性是为了节省计算资源,尽管这种形式的稀疏性,从理论上会造成一些可怕的输出间断性,但在实际使用中,我们并没有观察到这种问题。
每个分量的噪音量,通过另一个可训练的权重矩阵 $W_{\text {noise }}$ 来控制。
\begin{equation}
G(x)=\operatorname{Softmax}(\operatorname{KeepTopK}(H(x), k))
\end{equation}
\begin{equation}
H(x)_{i}=\left(x \cdot W_{g}\right)_{i}+\text { StandardNormal }() \cdot \operatorname{Softplus}\left(\left(x \cdot W_{\text {noise }}\right)_{i}\right)
\end{equation}
\begin{equation}
\text { KeepTopK }(v, k)_{i}=\left\{\begin{array}{ll}
v_{i} & \text { if } v_{i} \text { is in the top } k \text { elements of } v . \\
-\infty & \text { otherwise. }
\end{array}\right.
\end{equation}
训练门控网络
我们使用简单的反向传播来训练门控网络以及接下来的模型。
3 解决性能挑战
3.1 批量减小问题(The Shrinking Batch Problem)
由于门控网络对每个样本,在 $n$ 个专家中,选择 $k$ 个。那么对于 $b$ 个样本的批次,每个转接都会收到更加更加小的批次(大概 $\frac{k b}{n} \ll b$)。这会导致朴素的 MoE 实现在专家数量增加时,非常低效。解决批量减小问题,就是需要让原始的批量大小尽可能的大。然而,批量大小会收到内存的限制。我们提出如下技术来提高批量大小:
- 混合数据并行和模型并行(Mixing Data Parallelism and Model Parallelism)
- 充分利用卷积
- 增加循环 MoE 的批量大小
3.2 网络带宽
4 平衡专家的利用率
我们观察到,门控网络倾向于收敛到一种不好的状态,即对相同的少量专家,总是会得到较大的权重。这种不平衡是不断自我强化的,随着更好的专家不断训练学习,它们更有可能被门控网络选中。面对这种问题,过去文献有的用硬性约束,有的用软性约束。
而我们采用软性约束方法。我们定义对于一个批次训练样本的专家重要度(the importance of an expert),即该专家在一个批次上的门控输出值的和。并且定义损失项 $L_{\text {importance }}$,加入到模型的总损失上。该损失项等于所有专家重要度的方差的平方,再加上一个手工调节的比例因子 $w_{important}$。这个损失项会鼓励所有专家有相同的重要度。
\begin{equation}
\text { Importance }(X)=\sum_{x \in X} G(x)
\end{equation}
\begin{equation}
L_{\text {importance }}(X)=w_{\text {importance }} \cdot C V(\text { Importance }(X))^{2}
\end{equation}
尽管现在的损失函数可以保证相同的重要度,专家仍然可能接收到差异很大的样本数目。例如,某些专家可能接收到少量的大权重的样本;而某些专家可能接收到更多的小权重的样本。为了解决这个问题,我们引入了第二个损失函数:$L_{\text {load }}$,它可以保证负载均衡。附录 A 会包含该函数的定义。
5 实验
5.1 10 亿词汇的语言建模基准
5.2 1000 亿词汇的谷歌新闻语料库
5.3 机器翻译
5.4 多语言机器翻译
6 结论
- 该工作是第一个展现基于深度网络的条件计算的重大胜利。
- 我们探讨了设计考虑、条件计算的挑战、从算法和工程上的解决方案。
- 虽然我们聚焦在文本领域上,条件计算仍然可以在其他领域发挥作用。我们期望有更多条件计算的实现和应用。


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号