在本系列上一篇《【几何系列】复数基础与二维空间旋转》讲述了复数和二维旋转之间的联系。
在本文,向量是线性代数中的基本知识,本文只会侧重它们在计算机图形学和旋转几何学中的要点。
向量的记号
向量(vector)常用粗体来表示,与标量相区分(不过我为了方便,仅在此处加粗体)。例如:
$$\mathbf{u}=\begin{bmatrix}
2\\
3
\end{bmatrix}$$
其中 2 和 3 都称为向量 $\mathbf{u}$ 的分量(component)。向量还可以分为列向量和行向量,列向量常常是推荐的表示方法。
向量的图示
向量作为一种代数元素,在计算机图形学中常用于表示空间中的有向线段和点。
如下图所示:

利用向量的表示,有向线段 $u$ 可以通过 $A$ 和 $B$ 两点相减计算得到:
$$\mathbf{u}=\begin{bmatrix}
3\\
4
\end{bmatrix}-\begin{bmatrix}
1\\
1
\end{bmatrix}=\begin{bmatrix}
2\\
3
\end{bmatrix}$$
可以看到,对于有向线段 $u$ 来说,它的向量表示保存了两条信息:方向和长度。而对于坐标点 $A$ 和 $B$ 来说,实际上也隐含了两条类似的信息:原点到坐标点的方向和原点到坐标点的距离长度。方向通过向量各分量的比例而确定,而长度则是通过向量大小(magnitude)确定。
向量大小
向量大小写作 $\left | u \right |$,对分量应用毕达哥拉斯定理(国内称勾股定理)计算得到:
$$\left | u \right |=\sqrt{x^2+y^2}$$
其中 $x$ 和 $y$ 表示 $u$ 的两个分量。
推广到三维
前面考虑的是二维平面,如果推广到三维,则可以用向量表示出三维空间的点或有向线段:
$$u=\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}$$
其大小为:
$$\left | u \right |=\sqrt{x^2+y^2+z^2}$$
单位向量
前面说到,向量包含方向和大小的信息。那如果我们只关注方向信息呢?自然会想到把大小固定下来,进而引入了单位向量。
单位向量就是大小为 1 的向量,把普通向量转换为单位向量的过程称为规范化或标准化(normalization)。
向量的规范化很容易,将向量除以它的大小即可。
$$\hat{u}=\frac{u}{\left | u \right |}$$
其中 $\hat{u}$ 是 $u$ 所对应的单位向量。
笛卡尔向量
笛卡尔向量是特殊的单位向量,对应于笛卡尔坐标系中的 x/y/z 轴。即:
$$i=[1,0,0]^T,j=[0,1,0]^T,k=[0,0,1]^T$$
向量乘法
有两种向量乘法的定义,一种是两个向量相乘得到一个标量,称为标量积,又称点乘、点积、数量积;另一种是两个向量相乘得到一个向量,称为向量积,又称叉乘、叉积、矢量积。
标量积
标量积通过两个向量相乘得到一个标量。标量积的几何定义为:
$$r\cdot s=\left | r \right |\left | s \right |cos\beta $$

简单来说,就是向量 $r$ 对 $s$ 作投影,得到 $rcos\beta$,再将投影的大小 $\left | r \right |cos\beta$ 和 $s$ 向量的大小 $\left | s \right |$ 相乘(可以交换,不管哪个向量对另一个向量作投影结果都是相同的)。
标量积的设计是有道理的。
一方面,标量积在一定程度衡量了两个向量方向的“相似性”。固定大小的两个向量,夹角越小,方向越接近,相似度越高。
另一方面,标量积既然得到的是一个标量,向量又是标量的一种推广,我们自然希望它和普通标量的乘法统一起来。
与标量不同的是,向量具有方向性。那么在设计标量积的时候,一些显然需要考虑的场景是:
- 当两个向量方向一致时,我们希望这个标量积就等于两个向量大小的乘积。
- 当两个向量方向相反时,我们希望这个标量积等于向量方向一致情况的相反数。
- 当两个向量相互垂直(正交)时,这两个向量其实是线性无关的,我们认为它们俩其实没啥交流语言(或者说相似性为 0),乘积为 0 最好。
利用以上特殊场景,当面对更普遍的情况时,对向量进行正交分解,不难得到 $r\cdot s=\left | r \right |\left | s \right |cos\beta $ 的定义。
当然,这只是定义而已,前面这些考虑都只是为了帮助理解这个定义的几何含义。
标量积还有它的代数定义:
$$r\cdot s=r_xs_x+r_ys_y+r_zs_z$$
即两个向量的各个分量分别相乘,再相加。
标量积的几何定义和代数定义在笛卡尔坐标系上是等价的。即:从几何定义出发可以推导出代数定义,而从代数定义也可以推导出几何定义。
这两种定义给了我们两条解决问题的路径,显然,利用数量积作为桥梁,求两个向量的夹角也变得容易起来:
$$\beta =arccos(\frac{r_xs_x+r_ys_y+r_zs_z}{\left | r \right |\left | s \right |})$$
马里奥赛车里面的标量积应用:

要获得最大程度的加速效果,开车的方向要与加速板的方向尽可能一致,对加速板方向的投影大小要尽可能大。
向量积
向量积通过两个向量相乘得到另一个向量。
向量积定义为:
$$\left |a \right |\times \left | b \right |=\left | t \right |$$
其中 $t$ 的向量大小为:
$$\left | t \right |=\left |a \right | \left | b \right |sin\theta$$
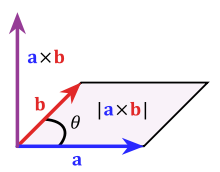
由于向量积得到的一个向量,那么向量就会有方向和大小两条信息。
对于向量 $t$ 的大小,如上图所示,向量积大小等于两个向量张成的平行四边形的面积。该面积衡量了两个向量的差异性(difference)。如果 $a$ 和 $b$ 是垂直(正交)的,两者的差异性最大,在两个向量大小不变的情况此时面积最大($sin\theta=1$);如果 $a$ 和 $b$ 是共线的,两者的差异性最小,此时面积等于 0。
对于向量 $t$ 的方向,考虑的是这样的问题:两个向量虽然张成的面积一样,但是方向却可能不同,只考虑张成的平行四边形面积大小会丢失掉这样的差异。例如笛卡尔向量,如果只考虑面积大小,$i\times j$ 和 $i\times k$ 得到的结果是完全一样的,但是 $j$ 和 $k$ 却是不同的方向。因此为了添加这个方向信息,如下图所示,通常采用右手法则(一种约定,区别于左手法则),规定了向量积 $t$ 的方向,即垂直于 $a$ 和 $b$ 张成的平面。于是 $i\times j$ 和 $i\times k$ 虽然向量大小相同,向量方向却不同。

向量积不满足交换律,但满足反对称关系:

根据这种关系,可以很容易知道笛卡尔向量的计算规律:
$$i\times j=k$$
$$j\times i=-k$$
$$j\times k=i$$
$$k\times j=-i$$
$$k\times i=j$$
$$i\times k=-j$$
我们还知道同一向量的向量积为 0(因为夹角 $\theta$ 为 0):
$$i\times i=0$$
$$j\times j=0$$
$$k\times k=0$$
基于以上关系,我们可以推导出向量积的代数计算公式。
已知两个向量 $a=a_xi+a_yj+a_zk$ 和 $b=b_xi+b_yj+b_zk$,计算:
\begin{align*}
a\times b &= (a_xi+a_yj+a_zk)\times(b_xi+b_yj+b_zk)\\
&=a_xb_xi\times i + a_yb_yj\times j+a_zb_zk\times k+a_xb_yi\times j+a_xb_zi\times k+a_yb_xj\times i+a_yb_zj\times k+a_zb_xk\times i+a_zb_yk\times j\\
&=0+0+0+a_xb_yk-a_xb_zj-a_yb_xk+a_yb_zi+a_zb_xj-a_zb_yi\\
&=(a_yb_z-a_zb_y)i+(a_zb_x-a_xb_z)j+(a_xb_y-a_yb_x)k\\
&=\begin{vmatrix}
a_y & a_z\\
b_y & b_z
\end{vmatrix}i-\begin{vmatrix}
a_x & a_z\\
b_x & b_z
\end{vmatrix}j+\begin{vmatrix}
a_x & a_y\\
b_x & b_y
\end{vmatrix}k \\
&=\begin{vmatrix}
i & j & k\\
a_x & a_y & a_z\\
b_x & b_y & b_z
\end{vmatrix}
\end{align*}
最后两步使用了行列式进行整理。最后,我们把向量积的定义和代数计算公式结合起来就是:
\begin{align*}
\mathbf{a}\times \mathbf{b} &= \left | \mathbf{a} \right |\left | \mathbf{b} \right |sin\theta \hat{\mathbf{t}} \\
&=\begin{vmatrix}
i & j & k\\
a_x & a_y & a_z\\
b_x & b_y & b_z
\end{vmatrix}\\
&=\begin{vmatrix}
a_y & a_z\\
b_y & b_z
\end{vmatrix}i-\begin{vmatrix}
a_x & a_z\\
b_x & b_z
\end{vmatrix}j+\begin{vmatrix}
a_x & a_y\\
b_x & b_y
\end{vmatrix}k
\end{align*}
$\hat{\mathbf{t}}$ 表示满足右手定则的单位法向量。
向量插值
这里仅讨论两种向量插值技术:线性插值和球形插值。线性插值的路径是直线,球形插值的路径是圆形或者曲线。
线性插值
线性插值非常直观,已知两个向量,给这两个向量各分配一个权重相加,权重和为 1。令插值得到的向量为 $v(t)$,则
$$v(t)=(1-t)v_1+tv_2=v_1+t(v_2-v_1)$$
其中 $t\in [0,1]$,当 $t=0$ 时,$v(t)=v_1$,当 $t=1$ 时,$v(t)=v_2$。
根据上式中的第二个等号,可以利用几何的方法推断出插值的路径:

$(v_2-v_1)$ 就是 $v_1$ 箭头端点指向 $v_2$ 箭头端点的向量,而 $t(v_2-v_1)$ 的箭头端点就在这个向量表示的线段上移动。通过与 $v_1$ 相加后发现,插值出来的 $v(t)$ 的箭头端点也在这条线段上,这就是线性插值的路径。
通过图示我们可以看到,这种线性插值在当两个向量大小相等时,无法保证插值向量的大小不变,在很多应用中我们其实希望这个向量大小是稳定的。比如 $v_1$ 和 $v_2$ 假设表示一条手臂在 $t_1$ 时刻和 $t_2$ 时刻的位置状态的话,我们希望插值得到 $t_1$ 和 $t_2$ 时刻之间的手臂的位置状态,如果用线性插值,我们会发现这个本来长度固定不变的手臂,插值后长度竟然发生变化了。
这就引入了球形插值。
球形插值
球形插值的推导过程暂且不表,但是其核心思想是加入了这样的限制条件:两个单位向量插值出来必然也是单位向量,进而保证了我们希望长度稳定的需求。
如果两个向量大小相同,它的插值路径是圆形;如果向量大小不同,则插值路径是曲线。一些例子:
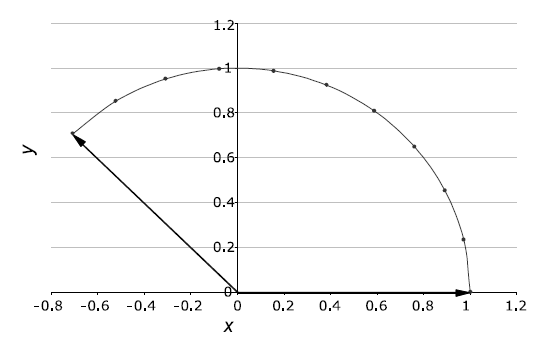
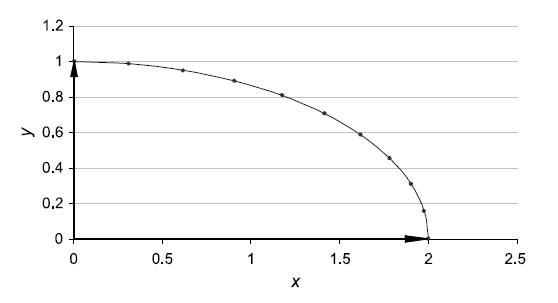
插值公式如下:
$$v(t)=\frac{sin(1-t)\theta}{sin\theta}v_1+\frac{sint\theta}{sin\theta}v_2$$
其中,$t\in [0,1]$,当 $t=0$ 时,$v(t)=v_1$,当 $t=1$ 时,$v(t)=v_2$。而 $\theta$ 是 $v_1$ 和 $v_2$ 的夹角,可以通过点乘的公式计算余弦。
参考
- 维基百科:数量积
- 维基百科:叉积
- Vector Calculus: Understanding the Dot Product
- Vector Calculus: Understanding the Cross Product
- 探讨:向量(方向)之间的插值-四元数法VS.旋转矩阵法的性能比较
- 《Rotation Transforms for Computer Graphics》by John Vince



 posted on
posted on

