本文我们讨论复数及其旋转的含义。复数很有意思,本文介绍了复数的基本定义和性质,以及它关于旋转的几何意义。
复数对于旋转的表示非常重要:
1. 它引入了旋转算子(rotational operator)的思想:可以通过复数表示一个旋转变换。
2. 它是四元数和多向量的内在属性。
虽然我们暂时不讨论四元数和多向量(后面文章会介绍),但是我们会讨论复数的旋转含义(复平面上的 2D 旋转),以及引入的旋转子(rotor),我们发现通过特定的复数可以描述一个 2D 旋转。
介绍
复数(complex number)又称为数字王国中的“国王”,它可以解决普通实数不能很好解决的问题。
例如,对于以下方程:
$$x^2+1=0$$
尽管方程如此简单,但并没有实数解。实际上,实数无法解决这样的问题:
$$x=\sqrt{-1}$$
但这没有妨碍数学家们找到解决此类问题的方法,他们提出一个很牛很简单的思想,就是承认 $i$ 的存在,它满足 $i^2=-1$,于是前面的方程我们可以解出:
$$x=\pm i$$
那么 $i$ 到底是什么呢?我们可以不必纠结,$i$ 就是数学家提出的数学工具,一个简单的数学对象,满足 $i^2=-1$。本文会探讨这个数学工具对于旋转如何发挥作用。
复数基础
复数的定义
复数由两个部分组成:实部(real part)和虚部(imaginary part)。实部就是我们平常遇到的数(正数、负数、0),而虚部是一个实数和 $i$ 的乘积。
例如,$2+3i$ 是一个复数,2 是实部,$3i$ 是虚部。
复数集就像是实数集的扩展,它包含了所有实数(虚部为 0)。而虚部不为 0 的复数不是实数。以下都属于复数:
- 2
- $2+2i$
- $1-3i$
- $-4i$
- $17i$
- $isin\theta$
- $4.5+icos\theta$
不过在 Python 中,复数的 $i$ 符号用 $j$ 表示,在 Jupyter 中运行 Python:
1 z = 3 + 4j 2 z, z.real, z.imag # 复数、实部、虚部
输出:
((3+4j), 3.0, 4.0) 5.0
复数的公理
下面的公理体现了复数的性质。对于任意的复数 $z_1$、$z_2$ 和 $z_3$,满足:
- 加法交换律:$z_1+z_2=z_2+z_1$
- 加法结合律:$(z_1+z_2)+z_3=z_1+(z_2+z_3)$
- 乘法交换律:$z_1z_2=z_2z_1$
- 乘法结合律:$(z_1z_2)z_3=z_1(z_2z_3)$
- 乘法分配律:$z_1(z_2+z_3)=z_1z_2+z_1z_3$、$(z_1+z_2)z_3=z_1z_3+z_2z_3$
其实复数的这些加法和乘法的公理和实数一样的。由于复数集里面包含实数集,如果不和实数一致,反而比较奇怪的。
复数的模
模(modulus)有长度的含义。对于复数 $z=a+bi$,它的模定义为:
$$\left | z \right |=\sqrt{a^2+b^2}$$
例如,$3+4i$ 的模为 5。
后面我们会看到,模定义在复数的极坐标表示中的作用。
例子:
abs(3 + 4j) # 模
输出:
5.0
复数的加减
对于两个复数:$z_1=a+bi$ 和 $z_2=c+di$,其加减法为
$$z_1\pm z_2=(a\pm c)+(b\pm d)i$$
即实部和虚部分别相加减。
例子:
(2 + 3j) + (3 - 4j) # 加法
输出:
(5-1j)
复数的标量乘法
标量乘法同样符合我们的直觉。对于标量 $\lambda$ 和复数 $a+bi$,有
$$\lambda(a+bi)=\lambda a+\lambda bi$$
例如:
$$2(3+5i)=6+10i$$
2 * (3 + 5j) # 标量乘法
输出:
(6+10j)
两个复数的乘积
两个复数的乘积就是各项分别相乘并相加。对于两个复数 $z_1=a+bi$ 和 $z_2=c+di$,有
\begin{align*}
z_1z_2 &= (a+bi)(c+di)\\
&= ac+adi+bci+bdi^2\\
&= (ac-bd)+(ad+bc)i
\end{align*}
例如,对于 $z_1=3+4i$ 和 $z_2=5-2i$,有
\begin{align*}
z_1z_2 &= (3+4i)(5-2i)\\
&= 15-6i+20i-8i^2\\
&= 23+14i
\end{align*}
可以看到。两个复数的加减和乘积都是一个复数。
(3 + 4j) * (5 - 2j) # 两复数的乘法
输出:
(23+14j)
共轭复数
两个复数相乘还有个特殊情况:
\begin{align*}
(a+bi)(a-bi)&=a^2-b^2i \\
&= a^2+b^2
\end{align*}
其中 $a-bi$ 称作是 $a+bi$ 的共轭复数(conjugate complex number),又称复共轭、复数共轭。
更一般的定义,$z=a+bi$ 的共轭复数用 $\bar{z}$ 或 $z^*$ 表示,其中:
$$z^*=a-bi$$
而
$$zz^*=a^2+b^2=\left |z \right |^2$$
例子:
(3 + 4j).conjugate() # 共轭复数
输出:
(3-4j)
两个复数的除法
利用共轭复数的性质,我们再来看复数的除法。
对于 $z_1=a+bi$ 和 $z_2=c+di$,其中 $z_2\neq 0$。
那么,
\begin{align*}
\frac{z_1}{z_2}&=\frac{z_1z_2^*}{z_2z_2^*} \\
&= \frac{z_1z_2^*}{\left | z_2 \right |^2} \\
&= \frac{(a+bi)(c-di)}{c^2+d^2} \\
&= \frac{(ac+bd)+(bc-ad)i}{c^2+d^2}
\end{align*}
例子:
\begin{align*}
\frac{4+3i}{3+4i}&=\frac{(4*3+3*4)+(3*3-4*4)i}{3^2+4^2} \\
&= \frac{24}{25}-\frac{7}{25}i
\end{align*}
(4 + 3j) / (3 + 4j) # 两复数的除法
输出:
(0.96-0.28j)
复数的逆
已知一个复数 $z\neq 0$,定义它的逆 $z^{-1}=\frac{1}{z}$。利用共轭复数的性质,我们可以推导:
$$\frac{z^{-1}}{z^*}=\frac{1}{zz^*} = \frac{1}{\left | z \right |^2}$$
$$\Rightarrow z^{-1}=\frac{z^*}{\left | z \right |^2}$$
例子:
\begin{align*}
\frac{1}{3+4i} &=(3+4i)^{-1} \\
&= \frac{3-4i}{25} \\
&= \frac{3}{25}-\frac{4}{25}i
\end{align*}
检查:$(3+4i)(\frac{3}{25}-\frac{4}{25}i)=\frac{9}{25}-\frac{12}{25}i+\frac{12}{25}i+\frac{16}{25}=1$
1 / (3 + 4j) # 复数求逆
输出:
(0.12-0.16j)
复数与旋转
首先,考虑一条实数轴,想象对于一个实数而言,与它的相反数究竟有什么关系?
我们可以把相反数看成:原实数绕原点旋转了 180°。
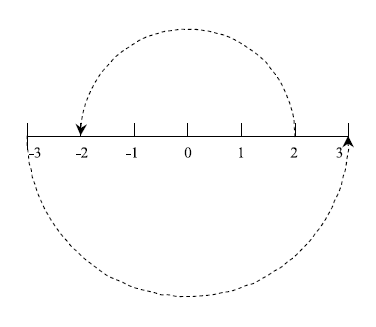
例如,“2” 旋转 180° 后变成 -2,“-3” 旋转 180° 后变成 “3”。由于复数的定义,我们可以把相反数 $-n$ 写成:
$$-n=i^2n$$
于是我们可以把乘以 $i^2$ 看成是绕原点 180° 的旋转。那么乘以 $i$ 表示什么呢?
90° 的旋转。
复平面
当我们用复数的实部和虚部构建一个 2D 坐标系,这就是复平面(complex plane)。复平面的横坐标表示实部,纵坐标表示虚部。
使用复平面,我们来观察这个 90° 的旋转是什么意思。
下面我们画出 4 个复数:$z_1=1+2i$、$z_2=-2+i$、$z_3=-1-2i$、$z_4=2-i$,它们分别可以代表 4 个长度相等的向量:$u$、$v$、$w$、$a$。之所以长度相等,是因为这 4 个复数的模相等。

我们可以看到它们依次逆时针旋转 90°。例如,
对 $u$ 旋转 90°:$i(1+2i)=-2+i=v$,得到 $v$。
对 $v$ 旋转 90°:$i(-2+i)=-1-2i=w$,得到 $w$。
对 $w$ 旋转 90°:$i(-1-2i)=2-i=a$,得到 $a$。
对 $a$ 旋转 90°:$i(2-i)=1+2i=u$,得到 $u$。
于是我们发现,要对一个复数(这个复数在复平面可以表示为一个 2D 向量)旋转 90°,只需乘以 $i$ 即可。
几百年前,Euler 通过复平面把复数画了出来,而其中蕴含的“复数可以表示旋转”的思想,在现在很多领域得到了应用。
极坐标表示
我们再整理一下上两节的内容。我们实际上发现:复数在几何上的有一些有意思的性质。
如果我们用复数来表示一个 2 维直角坐标系上的向量的话(当然复数是一个数学工具,也可以表示其他含义),看起来乘以 $i$ 表示旋转 90°。
那么自然地,我们就会去进一步思考,如果旋转任意角度应该怎么表达呢?旋转 45° 究竟是乘以 $\frac{1}{2}i$,还是乘以 $\sqrt{i}$,还是乘以其他的什么东西?
以及,为什么乘以复数会表示旋转?
为了解决这两个问题,我们开始引入复平面上的极坐标表示。
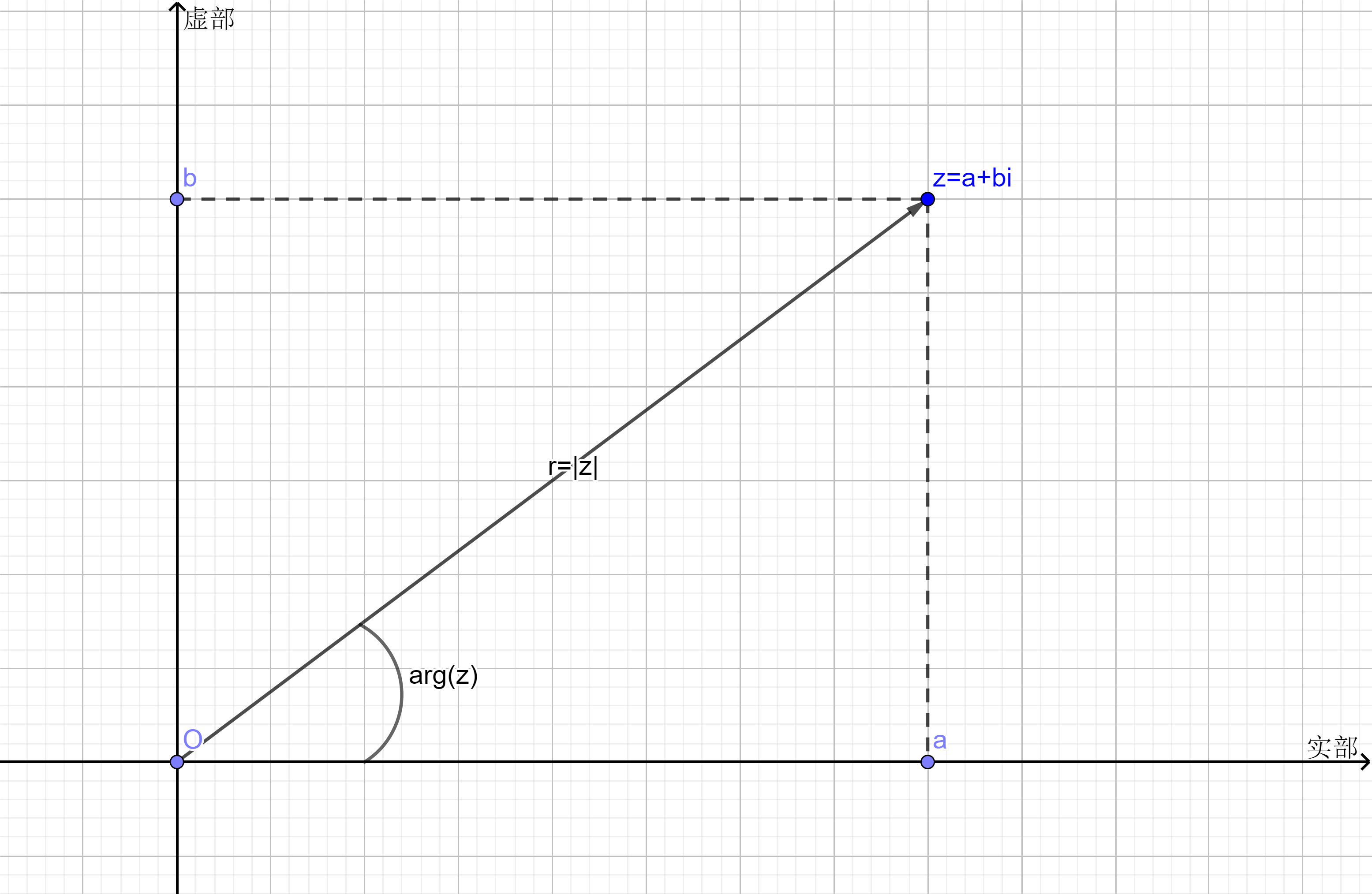
在这样的极坐标下,复数 $z=a+bi$ 可以通过长度 $\left r=| z \right |$ 和角度 $\theta=arg(z) $ 来唯一确定。
长度 $r$ 等于复数的模,而角度 $\theta$ 是实数轴和复数所表示的向量的夹角,称为幅角(argument),记为 $arg(z)$。接下来根据三角函数,我们有 $a=rcos\theta $ 和 $b=rsin\theta $,于是可以得到:
\begin{align*}
z&=a+bi \\
&=rcos\theta+irsin\theta \\
&=r(cos\theta+isin\theta)
\end{align*}
根据欧拉公式 $e^{i\theta}=cos\theta+isin\theta$,复数的极坐标表示可以写成更为简洁的形式:
$$z=re^{i\theta}$$
关于欧拉公式
Euler 提出的欧拉公式体现了自然底数 $e$ 和三角函数 $sin\theta$、$cos\theta$ 之间的关系。
关于它的含义一眼看去并不直观。欧拉方程的其中一种证明方法是利用泰勒级数展开式把 $e^x$ 、$cosx$ 和 $sinx$ 关联起来。以下是简单证明。
根据级数展开:
$$e^{i\theta}=1+(i\theta)+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+...$$
$$cos\theta=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+...$$
$$sin\theta=1-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+...$$
根据复数的定义 $i^2=-1$,于是有:
\begin{align*}
e^{i\theta} &= 1 + i\theta - \frac{\theta^2}{2!} - i\frac{\theta^3}{3!} + \frac{\theta^4}{4!}+i\frac{\theta^5}{5!}- \frac{\theta^6}{6!} - i\frac{\theta^7}{7!}+...\\
&= (1-\frac{\theta^2}{2!}+ \frac{\theta^4}{4!}- \frac{\theta^6}{6!}+...)+i(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+...) \\
&=cos\theta+isin\theta
\end{align*}
到了这种表达形式后,我们再看两个复数的乘法,就会发现它的几何含义。
给定两个任意用极坐标表示的复数:$z_1=r_1e^{i\theta _1}$ 和 $z_2=r_2e^{i\theta _2}$。那么我们会得到:
\begin{align*}
z_1z_2 &= r_1r_2e^{i\theta _1}e^{i\theta _2} \\
&= r_1r_2e^{i(\theta _1+\theta _2)}
\end{align*}
可以看到,两个复数的乘积得到另一个复数。
它的模等于两个复数的模的乘积:$\left | z_1z_2 \right |=r_1r_2$。
它的幅角等于两个复数的幅角的和:$arg(z_1z_2)=\theta _1+\theta _2$
于是看起来,考虑复平面这个几何情形,乘以一个复数,可以同时带来两种变换的效果。
1. 长度的缩放(通过改变模长)。
2. 旋转(通过改变幅角)。
旋转子
接下来一个很自然的想法,就是:乘以一个什么样的复数,不会产生缩放,只会产生旋转?
显然,通过前面极坐标下自然底数的表达形式的推导,我们知道乘以一个模为 1 的复数时,不会导致缩放,只会产生旋转。
这样的复数就称为旋转子(rotor),旋转子提供了“纯”旋转动作的数学表示,它可以将复数旋转任意角度。一般而言,将复数旋转角度 $\theta$ 的旋转子定义为:
$$R_\theta =cos\theta + isin\theta =e^{i\theta}$$
例如,对于复数 $2+2i$,我们如果需要对它进行逆时针 45° 的旋转,需要乘以:
$$1\cdot e^{i\cdot 45^{\circ}}=cos45^{\circ}+isin45^{\circ}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$$
我们通过手算计算出其乘积为 $2\sqrt{2}i$
$$(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)(2+2i)=\sqrt{2}+\sqrt{2}i+\sqrt{2}i+\sqrt{2}i^2=2\sqrt{2}i$$
如果通过 Python 计算会得到其对应的结果:
1 from math import pi, cos, sin 2 3 theta = pi / 4 # 定义角度 4 z1 = 2 + 2j 5 z2 = cos(theta) + 1j * sin(theta) 6 print(z1) 7 print(z2) 8 print(z1 * z2)
输出:
(2+2j) (0.7071067811865476+0.7071067811865476j) 2.8284271247461903j
通过下图,我们看到了旋转子的“纯”旋转效果。

接下来,我们看看旋转子的共轭复数是什么。由于旋转子模为 1,而根据前面共轭复数和逆的定义,我们不难证明:旋转子的共轭复数等于该旋转子的逆。
对于旋转子 $R_\theta=e^{i\theta}=cos\theta+isin\theta$,
它的共轭复数:$(R_\theta)^*=cos\theta-isin\theta=cos(-\theta)+isin(-\theta)=R_{-\theta}$
它的逆:$e^{i\theta}e^{-i\theta}=1\Rightarrow (R_\theta)^{-1}=e^{-i\theta}=R_{-\theta}$
那么接着前面的例子,$z_1$ 乘以 $z_2$ 的共轭复数(或者逆)后的效果,是顺时针旋转 45°。
$z_2$ 的共轭复数(或者逆)为:$R_{-\theta}=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$
手算:$(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)(2+2i)=\sqrt{2}-\sqrt{2}i+\sqrt{2}i-\sqrt{2}i^2=2\sqrt{2}$
用代码计算结果:
1 z3 = z2.conjugate() # z2 的共轭复数 2 print(z3) 3 print(z1 * z3)
输出:
(0.7071067811865476-0.7071067811865476j) (2.8284271247461903+0j)
最后再看看复平面图,确认复数 $z_1$ 沿着相反方向旋转 45°:
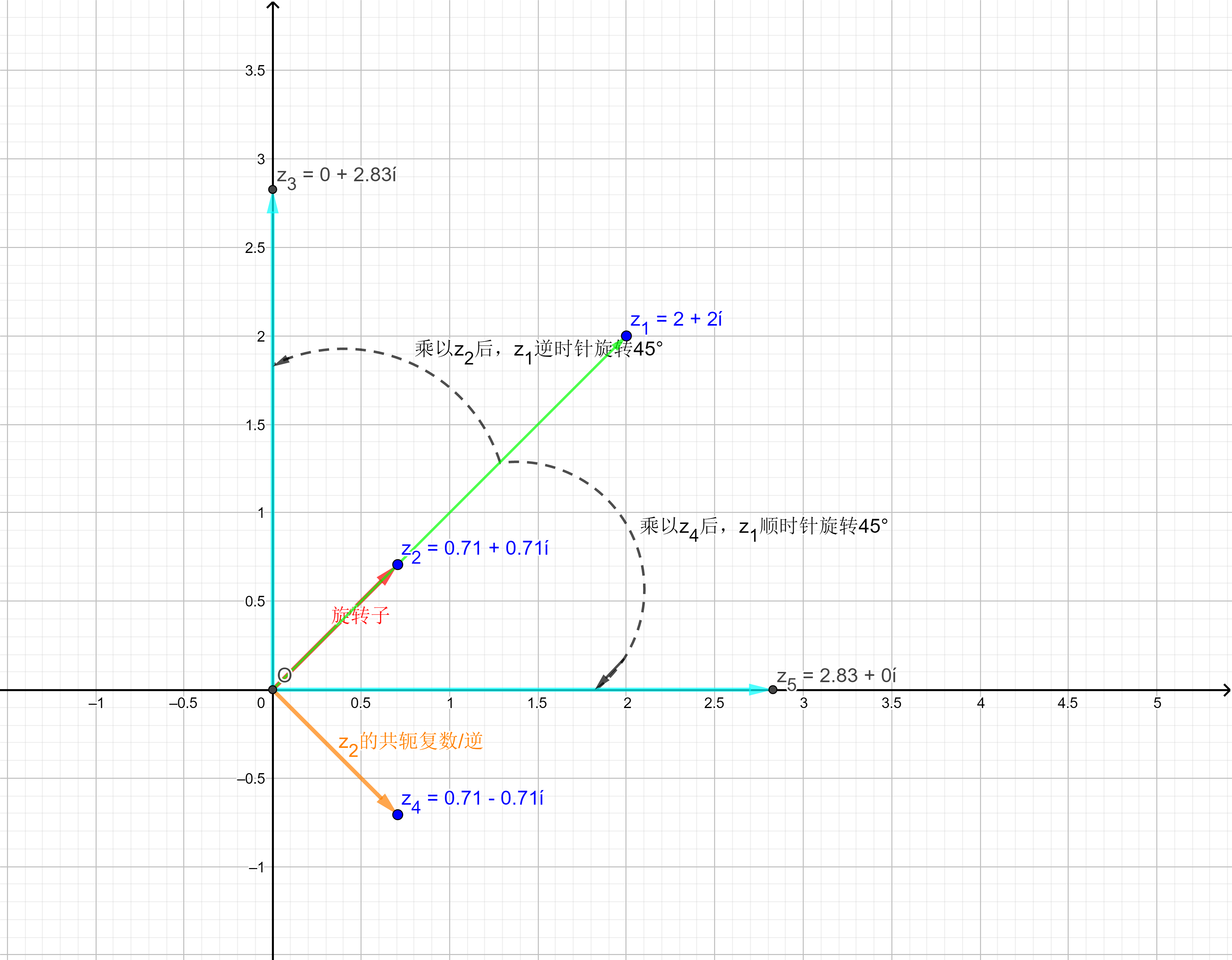
“逆”的含义也在于此,既然旋转子表示旋转任意角度,那么它的逆就应该是“抵消”这种旋转效果,于是它的作用就是朝相反的方向旋转对应的角度。
到此为止,我们已经可以用复数表示二维空间的任意旋转角度,并且利用复数的逆/共轭复数来表示旋转的抵消作用。后面我还会继续发布与旋转有关的文章。
原文作者:何雨龙
原文链接:https://www.cnblogs.com/noluye/p/11964513.html
许可协议:知识共享署名-非商业性使用 4.0 国际许可协议
总结
- 我们谈了复数的基础:复数的定义、公理、加减乘除、模、共轭复数、逆。复数域对实数域进行了很好的扩展,使我们可以去描述旋转。
- 我们定义了复平面,作为我们讨论的二维直角坐标系。
- 我们首先给出了复数的极坐标表示,并且利用欧拉公式推导出了等价的自然底数的表示。到了这一步,复数对于二维旋转的刻画性质已经呼之欲出。
- 复数的乘法运算表现了伸缩和旋转的两种性质,通过对模进行约束(模长等于 1),我们最终得到只表示旋转的复数,称为旋转子。
- 在旋转子中,共轭复数和逆是相等的,而逆表示相反方向的旋转。
参考
- Rotation Transforms for Computer Graphics by John Vince
- 欧拉公式



 posted on
posted on

