NumPy 是 Python 数值计算非常重要的一个包。很多科学计算包都是以 NumPy 的数组对象为基础开发的。

本文用代码快速过了一遍 NumPy 的基本操作，对 NumPy 整体有一个把握。希望能对读者有帮助。

NumPy ndarray：多维数组对象

ndarray 是 NumPy 很重要的特性，它是快速而灵活的数据集容器。ndarray 可以在整个数据集上进行类似于标量的运算，既快速又方便。

在 Jupyter Notebook 上，首先引入 NumPy 包：

1 import numpy as np

创建 ndarray，其中包含随机值（np.random.randn）：

1 np.random.seed(666)  # 设置随机种子
2 data = np.random.randn(2, 3)
3 data

array([[ 0.82418808,  0.479966  ,  1.17346801],
       [ 0.90904807, -0.57172145, -0.10949727]])

进行一些运算（乘法和加法）：

1 data * 10
2 data + data

array([[ 8.24188083,  4.79966003, 11.73468012],
       [ 9.09048069, -5.71721452, -1.09497268]])
array([[ 1.64837617,  0.95993201,  2.34693602],
       [ 1.81809614, -1.1434429 , -0.21899454]])

ndarray 所有的数据必须是相同类型，其属性 shape 表示形状大小，dtype 表示该数组的数据类型。

1 data.shape
2 data.dtype

(2, 3)
dtype('float64')

ndarray 的创建

最简单的创建方法是使用 array 函数。该函数根据接收的序列对象，生成新的 NumPy 数组。

1 data1 = [6, 66, 666, 6666, 66666]
2 arr1 = np.array(data1)
3 arr1

1 arr2.shape
2 arr2.ndim

array([    6,    66,   666,  6666, 66666])

嵌套的序列（比如说嵌套列表），可以生成多维的数组。

1 data2 = [[6, 66, 666], [6666, 66666, 666666]]
2 arr2 = np.array(data2)
3 arr2

array([[     6,     66,    666],
       [  6666,  66666, 666666]])

前面介绍了 ndarray 的属性 shape 表示形状大小，它还有一个属性 ndim 表示维度大小，我们可以对比两者的区别。

1 arr2.shape
2 arr2.ndim

(2, 3)
2

除了 np.array，还有一些函数可以创建新数组：zeros、ones、empty 等等。（注意到 empty 不一定返回零值，某些情况它可能返回未初始化的不确定值）

1 np.zeros(6)
2 np.ones([2, 3])
3 np.empty((2, 3, 2))

array([0., 0., 0., 0., 0., 0.])
Out[26]:
array([[1., 1., 1.],
       [1., 1., 1.]])
Out[26]:
array([[[0.00000000e+000, 0.00000000e+000],
        [2.96439388e-323, 0.00000000e+000],
        [2.14321575e-312, 1.58817677e-052]],

       [[6.50119216e-091, 1.74483574e-076],
        [1.28392645e+160, 1.35027265e+161],
        [3.99910963e+252, 9.02421558e-309]]])

np.arange 类似于 Python 的 range 函数，只不过它生成的是 ndarray。

1 np.arange(6)
2 np.array(range(6))  # arange 等价于该效果

array([0, 1, 2, 3, 4, 5])
array([0, 1, 2, 3, 4, 5])

ndarray 的数据类型

前面介绍的 dtype 可以在创建时指定：

1 arr1 = np.array([6, 66, 666], dtype=np.float64)
2 arr2 = np.array([6, 66, 666], dtype=np.int32)
3 arr1.dtype
4 arr2.dtype

dtype('float64')
dtype('int32')

一些典型的数据类型有：uint8、int32、float64、float128、complex64、bool、object、string_、unicode_ 等。

使用 astype 可以对数据类型进行显式转换。

1 arr = np.array([6, 66, 666])
2 arr.dtype
3 float_arr = arr.astype(np.float64)
4 float_arr.dtype

dtype('int64')
dtype('float64')

浮点数数组转为整型数组：

1 arr = np.array([1.7, 2.7, 3.7])
2 arr
3 arr.astype(np.int32)

array([1.7, 2.7, 3.7])
array([1, 2, 3], dtype=int32)

字符串数组转为浮点数数组（float 是 Python 类型，NumPy 自动解析识别）：

1 numeric_strings = np.array(['1.7', '-2.7', '3.7'], dtype=np.string_)
2 float_arr = numeric_strings.astype(float)
3 float_arr
4 float_arr.dtype

array([ 1.7, -2.7,  3.7])
dtype('float64')

使用其他数组的 dtype 属性来进行转换：

1 int_arr = np.arange(6)
2 int_arr
3 float_arr = np.array([6., 66., 666.], dtype=np.float64)
4 int_arr.astype(float_arr.dtype)

array([0, 1, 2, 3, 4, 5])
array([0., 1., 2., 3., 4., 5.])

ndarray 的算术运算

ndarray 的算术运算可以避免写 for 循环，这既方便，性能也好。

数组与相同大小的数组之间的运算：

1 arr = np.array([[1., 2., 3.], [4., 5., 6.]])
2 arr
3 arr * arr
4 arr - arr

array([[1., 2., 3.],
       [4., 5., 6.]])
array([[ 1.,  4.,  9.],
       [16., 25., 36.]])
array([[0., 0., 0.],
       [0., 0., 0.]])

数组与标量的运算，会按数组的元素一一进行计算。

1 1 / arr
2 arr ** 0.5

array([[1.        , 0.5       , 0.33333333],
       [0.25      , 0.2       , 0.16666667]])
array([[1.        , 1.41421356, 1.73205081],
       [2.        , 2.23606798, 2.44948974]])

相同大小的数组之间的比较运算，会返回布尔值的数组：

1 arr2 = np.array([[0., 4., 1.], [7., 2., 12.]])
2 arr2
3 arr
4 arr2 > arr

array([[ 0.,  4.,  1.],
       [ 7.,  2., 12.]])
array([[1., 2., 3.],
       [4., 5., 6.]])
array([[False,  True, False],
       [ True, False,  True]])

索引和切片

一维数组很简单，看起来类似于 Python 列表：

1 arr = np.arange(10)
2 arr
3 arr[5]
4 arr[5:8]
5 arr[5:8] = 12
6 arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])-
5
array([5, 6, 7])
array([ 0,  1,  2,  3,  4, 12, 12, 12,  8,  9])

第 5 行用到了 ndarray 的 broadcast 机制，这是和原生 Python 列表的第一个区别，我们可以看到列表会报错：

1 li = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
2 li
3 li[5]
4 li[5:8]
5 li[5:8] = 12
6 li

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
5
[5, 6, 7]
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-43-b59603238145> in <module>
      3 li[5]
      4 li[5:8]
----> 5 li[5:8] = 12
      6 li

TypeError: can only assign an iterable

ndarray 的切片（或索引）是一个指针（NumPy 称之为视图 view），不会复制底层数据，修改切片会直接影响到数组本身。

1 arr_slice = arr[5:8]
2 arr_slice
3 arr_slice[1] = 666
4 arr

array([12, 12, 12])
array([  0,   1,   2,   3,   4,  12, 666,  12,   8,   9])

切片 [:] 的赋值会影响到所有元素：

1 arr_slice[:] = 777
2 arr

array([  0,   1,   2,   3,   4, 777, 777, 777,   8,   9])

由于 NumPy 经常和大型数据集打交道，因此切片是指针并不奇怪。如果希望不影响原数组，应该使用 copy 方法。

1 arr_slice = arr[5:8].copy()
2 arr_slice[:] = 666
3 arr

array([  0,   1,   2,   3,   4, 777, 777, 777,   8,   9])

在二维数组中，每个索引代表的元素不再是标量。要找到每个元素有两种方法。

1 arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
2 arr2d[2]
3 # 法 1
4 arr2d[0][2]
5 # 法 2
6 arr2d[0, 2]

array([7, 8, 9])
3
3

在这样的二维数组中，axis 0 可以理解为行，axis 1 可以理解为列。

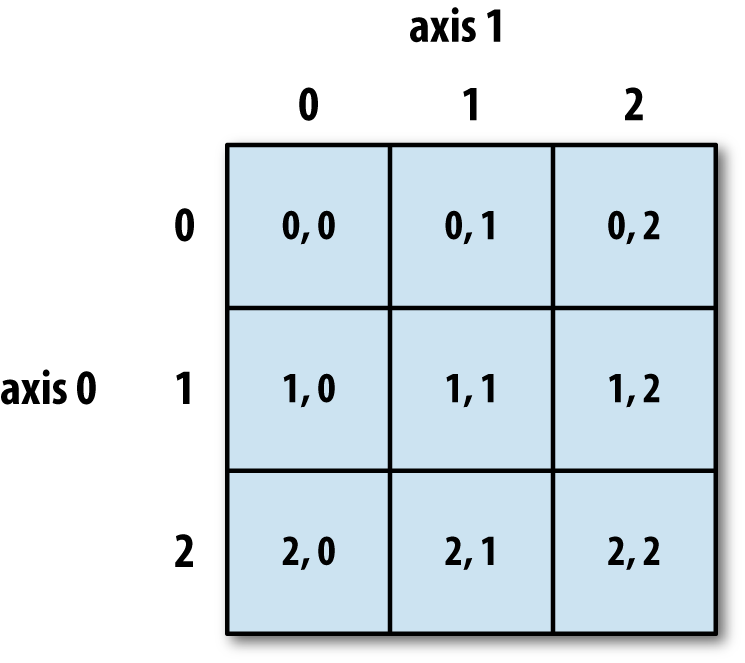
三维数组的使用示例：

1 arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
2 arr3d
3 arr3d[0]

array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])
array([[1, 2, 3],
       [4, 5, 6]])

标量和数组都可以赋值给 arr3d[0]：

1 old_values = arr3d[0].copy()
2 arr3d[0] = 666
3 arr3d
4 arr3d[0] = old_values
5 arr3d

array([[[666, 666, 666],
        [666, 666, 666]],

       [[  7,   8,   9],
        [ 10,  11,  12]]])
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

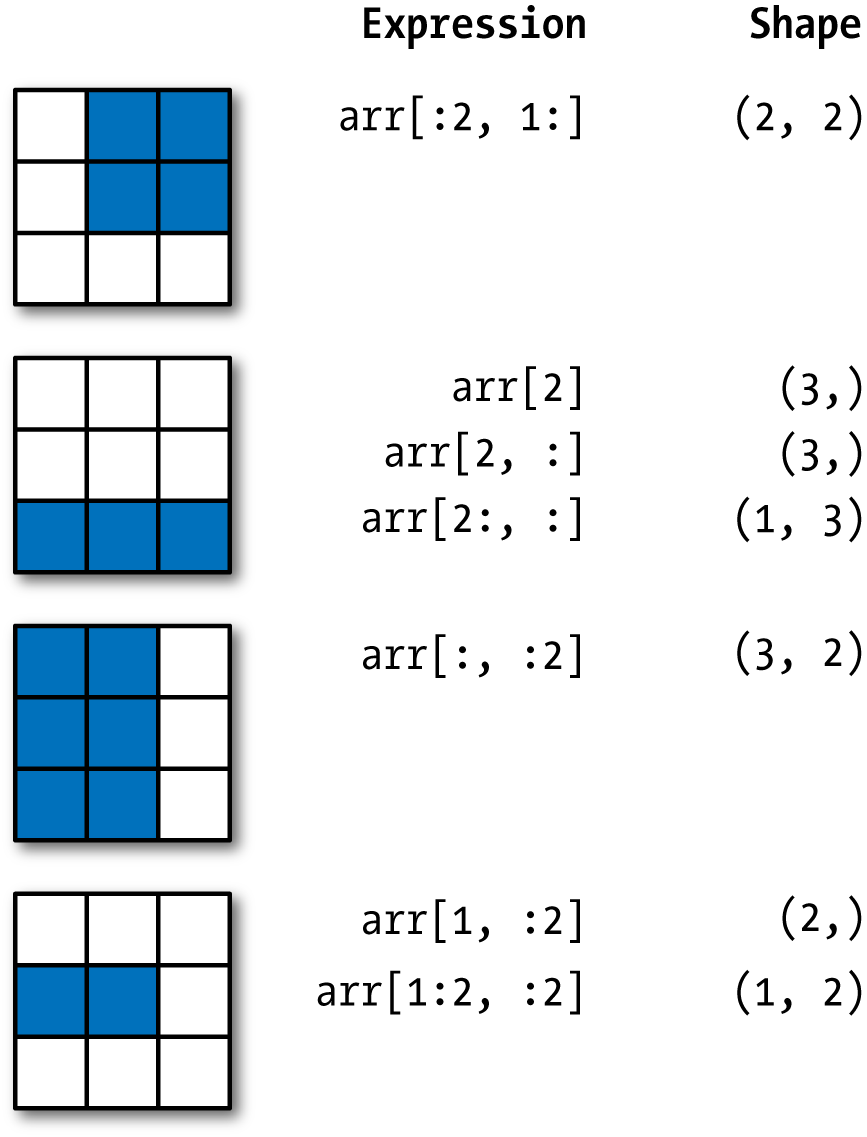
用切片进行索引

1 arr
2 arr[1:6]
3 arr2d
4 arr2d[:2]
5 arr2d[:2, 1:]

array([  0,   1,   2,   3,   4, 777, 777, 777,   8,   9])
array([  1,   2,   3,   4, 777])
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
array([[1, 2, 3],
       [4, 5, 6]])
array([[2, 3],
       [5, 6]])

注意，如果使用切片作为索引，得到的总是相同维度的视图，而如果使用索引，则必定得到的是低维的数组。

1 arr2d
2 # 使用切片
3 arr2d[1:2, :2]
4 # 使用了索引
5 arr2d[1, :2]
6 arr2d[:2, 2]

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
array([[4, 5]])
array([4, 5])
array([3, 6])

布尔索引

首先生成一些数据：

1 names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
2 np.random.seed(666)
3 data = np.random.randn(7, 4)
4 names
5 data

array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'], dtype='<U4')
array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525],
       [-1.75662522,  0.84463262,  0.27721986,  0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802]])

假设每个 name 对应着 data 中的每一行，我们希望选择 Bob 有关的数据。

1 names == 'Bob'
2 data[names == 'Bob']

array([ True, False, False,  True, False, False, False])
array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737]])

可以看到，选择了第 0 行和第 3 行的数据。需要注意的是布尔数组的长度必须和该维度的长度相同，否则会报错。

1 np.array([ True, False, False,  True, False, False, False])[:-1]
2 data[np.array([ True, False, False,  True, False, False, False])[:-1]]

array([ True, False, False,  True, False, False])
---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-72-07628751d568> in <module>
      1 np.array([ True, False, False,  True, False, False, False])[:-1]
----> 2 data[np.array([ True, False, False,  True, False, False, False])[:-1]]

IndexError: boolean index did not match indexed array along dimension 0; dimension is 7 but corresponding boolean dimension is 6

布尔索引结合切片或索引的情况：

1 data[names == 'Bob', 2:]
2 data[names == 'Bob', 3]

array([[ 1.17346801,  0.90904807],
       [-0.29873262, -0.46058737]])
array([ 0.90904807, -0.46058737])

要取反，可以使用 != 或者 ~：

1 data [names != 'Bob']
2 data[~(names == 'Bob')]

array([[-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525],
       [-1.75662522,  0.84463262,  0.27721986,  0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802]])
array([[-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525],
       [-1.75662522,  0.84463262,  0.27721986,  0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802]])

如果要结合多个布尔条件，使用布尔运算符 &（且）和 |（或）：

1 names
2 mask = (names == 'Bob') | (names == 'Will')
3 mask
4 data[mask]

array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'], dtype='<U4')
array([ True, False,  True,  True,  True, False, False])
array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525]])

注意：使用布尔进行索引后返回的数组总是是原数组的拷贝，而非指针，也没有 broadcast 机制。这是与索引或者切片所不同的地方。

1 data
2 data_copy = data[names == 'Bob']
3 data_copy
4 data_copy[:, :] = 666
5 data_copy
6 data

array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525],
       [-1.75662522,  0.84463262,  0.27721986,  0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802]])
array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737]])
array([[666., 666., 666., 666.],
       [666., 666., 666., 666.]])
array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737],
       [-1.08879299, -0.57577075, -1.68290077,  0.22918525],
       [-1.75662522,  0.84463262,  0.27721986,  0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802]])

但是注意是返回后的数组才是拷贝，可以用布尔索引来直接进行赋值，也可以使用 broadcast 机制。

1 data[names == 'Bob'] = 666
2 data

array([[ 6.66000000e+02,  6.66000000e+02,  6.66000000e+02,
         6.66000000e+02],
       [-5.71721452e-01, -1.09497268e-01,  1.90282649e-02,
        -9.43761065e-01],
       [ 6.40573153e-01, -7.86443172e-01,  6.08869993e-01,
        -9.31011849e-01],
       [ 6.66000000e+02,  6.66000000e+02,  6.66000000e+02,
         6.66000000e+02],
       [-1.08879299e+00, -5.75770746e-01, -1.68290077e+00,
         2.29185248e-01],
       [-1.75662522e+00,  8.44632619e-01,  2.77219863e-01,
         8.52901533e-01],
       [ 1.94599603e-01,  1.31063772e+00,  1.54384360e+00,
        -5.29048024e-01]])

fancy 索引

fancy 索引在 NumPy 中指的是使用整型数组来进行索引。

假设有以下一个 ndarray：

1 arr = np.empty((8, 4))
2 for i in range(8):
3     arr[i] = i
4 arr

array([[0., 0., 0., 0.],
       [1., 1., 1., 1.],
       [2., 2., 2., 2.],
       [3., 3., 3., 3.],
       [4., 4., 4., 4.],
       [5., 5., 5., 5.],
       [6., 6., 6., 6.],
       [7., 7., 7., 7.]])

使用 fancy 索引可以选择行的顺序：

1 arr[[7, 6, 5, 4, 3, 2, 1, 0]]
2 arr[[-1, 0]]

array([[7., 7., 7., 7.],
       [6., 6., 6., 6.],
       [5., 5., 5., 5.],
       [4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [2., 2., 2., 2.],
       [1., 1., 1., 1.],
       [0., 0., 0., 0.]])
array([[7., 7., 7., 7.],
       [0., 0., 0., 0.]])

如果传入多个索引数组的话，会针对每个既定顺序的行，选择既定顺序的列，最终得到几个元素的数组。

1 arr = np.arange(32).reshape((8, 4))
2 arr
3 arr[[3, 2, 1, 0], [3, 2, 1, 0]]

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])
array([15, 10,  5,  0])

下面示例的效果是变换数组所选行和列的顺序，而不会降维。

1 arr[[3, 2, 1, 0]][:, [3, 2, 1, 0]]

array([[15, 14, 13, 12],
       [11, 10,  9,  8],
       [ 7,  6,  5,  4],
       [ 3,  2,  1,  0]])

注意：fancy 索引同样返回的是数组的拷贝，而非指针。

数组的转置和轴的交换

转置（.T）返回的是底层数组的视图，而非数组的拷贝。

1 arr = np.arange(15). reshape((3, 5))
2 arr
3 arr.transpose()  # 转置
4 arr.T  # 更简便的写法

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])
array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

矩阵的内积计算使用 np.dot：

1 arr1 = np.array([[3, -1], [1, 2]])
2 arr1
3 arr2 = np.array([[2, 1]])
4 arr2
5 np.dot(arr1, arr2.T)

array([[ 3, -1],
       [ 1,  2]])
array([[2, 1]])
array([[5],
       [4]])

transpose 可以接收元组参数来交换轴：

 1 arr = np.arange(6).reshape((2, 3))
 2 arr
 3 arr.transpose((0, 1))
 4 arr.transpose((1, 0))
 5 arr = np.arange(16).reshape((2, 2, 4))
 6 arr
 7 # 置换 axis=1 和 axis=0, axis=2 不变
 8 # 由于 axis=2 不变，那么
 9 # 设 a = [0, 1, 2, 3] b = [4, 5, 6, 7] c = [8, 9, 10, 11] d = [12, 13, 14, 15]
10 # arr = [[a, b], [c, d]]
11 # arr.transpose(1, 0) = arr.T = [[a, c], [b, d]] = [[[0, 1, 2, 3], [8, 9, 10, 11]], [[4, 5, 6, 7], [12, 13, 14, 15]]]
12 arr.transpose((1, 0, 2))

array([[0, 1, 2],
       [3, 4, 5]])
array([[0, 1, 2],
       [3, 4, 5]])
array([[0, 3],
       [1, 4],
       [2, 5]])
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
array([[[ 0,  1,  2,  3],
        [ 8,  9, 10, 11]],

       [[ 4,  5,  6,  7],
        [12, 13, 14, 15]]])

swapaxes 同样可以交换轴：

1 arr
2 arr.swapaxes(1, 2)
3 arr.transpose(0, 2, 1)  # 类似于 arr.swapaxes(1, 2)

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
array([[[ 0,  4],
        [ 1,  5],
        [ 2,  6],
        [ 3,  7]],

       [[ 8, 12],
        [ 9, 13],
        [10, 14],
        [11, 15]]])
array([[[ 0,  4],
        [ 1,  5],
        [ 2,  6],
        [ 3,  7]],

       [[ 8, 12],
        [ 9, 13],
        [10, 14],
        [11, 15]]])

注意 swapaxes 同样返回的是数组的视图，而不是数组的拷贝。

通用函数

通用函数执行的是按元素的运算。

sqrt 和 exp：

1 arr = np.arange(10)
2 arr
3 np.sqrt(arr)
4 np.exp(arr)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
       2.98095799e+03, 8.10308393e+03])

maximum 和 minimum：

1 np.random.seed(666)
2 x = np.random.randn(8)
3 x
4 y = np.random.randn(8)
5 y
6 np.maximum(x, y)
7 np.minimum(x, y)

array([ 0.82418808,  0.479966  ,  1.17346801,  0.90904807, -0.57172145,
       -0.10949727,  0.01902826, -0.94376106])
array([ 0.64057315, -0.78644317,  0.60886999, -0.93101185,  0.97822225,
       -0.73691806, -0.29873262, -0.46058737])
array([ 0.82418808,  0.479966  ,  1.17346801,  0.90904807,  0.97822225,
       -0.10949727,  0.01902826, -0.46058737])
array([ 0.64057315, -0.78644317,  0.60886999, -0.93101185, -0.57172145,
       -0.73691806, -0.29873262, -0.94376106])

典型的一元通用函数有：

abs, fabs
sqrt
square
exp
log, log10, log2, log1p
sign
ceil, floor, rint
modf
isnan
isfinite, isinf
cos, cosh, sin, sinh, tan, tanh
arccos, arccosh, arcsin, arcsinh, arctan, arctanh
logical_not

典型的二元通用函数有：

add
subtract
multiply
divide, floor_divide
power
maximum, fmax
minimum, fmin
mod
copysign
greater, greater_equal, less, less_equal, equal, not_equal
logical_and, logical_or, logical_xor

面向数组编程

直接面向数组编程可以避免使用 for 循环，这又称为向量化（vectorization），一般来说性能会好上一两个量级以上。

1 points = np.arange(-5, 5, 0.01)
2 xs, ys = np.meshgrid(points, points)
3 xs
4 ys

array([[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       ...,
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99]])
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ...,
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

1 z = np.sqrt(xs ** 2 + ys ** 2)
2 z

array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
        7.06400028],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       ...,
       [7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
        7.04279774],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568]])

这里使用 matplotlib 建立这个二维数组的数据可视化。

1 import matplotlib.pyplot as plt
2 
3 plt.imshow(z, cmap=plt.cm.gray)
4 plt.colorbar()
5 
6 plt.title('Image plot of $\sqrt{x^2 + y^2}$ for a grid of values')

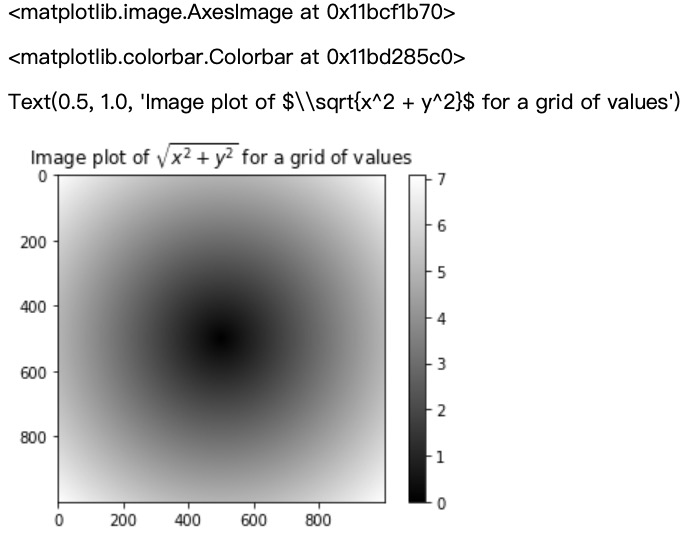
带条件逻辑的数组运算

numpy.where 函数是 x if condition else y 的向量化版本。

1 x = np.array([6, 66, 666, 6666, 66666])
2 y = np.array([7, 77, 777, 7777, 77777])
3 cond = np.array([True, False, True, True, False])
4 result = np.where(cond, x, y)
5 result

array([    6,    77,   666,  6666, 77777])

典型的使用场景：

1 np.random.seed(666)
2 arr = np.random.randn(4, 4)
3 arr
4 arr > 0
5 np.where(arr > 0, 1, -1)  # 对两种情况都赋值
6 np.where(arr > 0, arr, 0)  # 只处理小于零的情况

array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737]])
array([[ True,  True,  True,  True],
       [False, False,  True, False],
       [ True, False,  True, False],
       [ True, False, False, False]])
array([[ 1,  1,  1,  1],
       [-1, -1,  1, -1],
       [ 1, -1,  1, -1],
       [ 1, -1, -1, -1]])
array([[0.82418808, 0.479966  , 1.17346801, 0.90904807],
       [0.        , 0.        , 0.01902826, 0.        ],
       [0.64057315, 0.        , 0.60886999, 0.        ],
       [0.97822225, 0.        , 0.        , 0.        ]])

数学和统计运算

典型的聚合函数有：sum，mean，std。

1 np.random.seed(666)
2 arr = np.random.randn(6, 6)
3 arr
4 arr.mean()
5 np.mean(arr)
6 arr.sum()
7 arr.std()

array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807, -0.57172145,
        -0.10949727],
       [ 0.01902826, -0.94376106,  0.64057315, -0.78644317,  0.60886999,
        -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737, -1.08879299,
        -0.57577075],
       [-1.68290077,  0.22918525, -1.75662522,  0.84463262,  0.27721986,
         0.85290153],
       [ 0.1945996 ,  1.31063772,  1.5438436 , -0.52904802, -0.6564723 ,
        -0.2015057 ],
       [-0.70061583,  0.68713795, -0.02607576, -0.82975832,  0.29655378,
        -0.3126795 ]])
-0.03691228536732661
-0.03691228536732661
-1.328842273223758
0.81811319613762

mean 和 sum 有一个 axis 参数用于指定针对哪一行：

1 arr.mean(axis=1)
2 arr.sum(axis=0)

array([ 0.45090857, -0.23212411, -0.36376326, -0.20593112,  0.27700915,
       -0.14757295])
array([-0.3674784 ,  1.0262478 ,  1.27645117, -0.8521562 , -1.13434309,
       -1.27756353])

一些典型的统计性方法：

sum
mean
std, var
min, max
argmin, argmax
cumsum
cumprod

布尔数组的方法

any 检查某数组是否有一个以上的 True，all 检查某数组是否所有值都为 True。

1 bools = np.array([False, False, True, False])
2 bools.any()
3 bools.all()

True
False

排序

1 np.random.seed(666)
2 arr = np.random.randn(6)
3 arr
4 arr.sort()
5 arr

array([ 0.82418808,  0.479966  ,  1.17346801,  0.90904807, -0.57172145,
       -0.10949727])
array([-0.57172145, -0.10949727,  0.479966  ,  0.82418808,  0.90904807,
        1.17346801])

针对某一维度进行排序：

1 np.random.seed(666)
2 arr = np.random.randn(5, 3)
3 arr
4 arr.sort(1)
5 arr

array([[ 0.82418808,  0.479966  ,  1.17346801],
       [ 0.90904807, -0.57172145, -0.10949727],
       [ 0.01902826, -0.94376106,  0.64057315],
       [-0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262]])
array([[ 0.479966  ,  0.82418808,  1.17346801],
       [-0.57172145, -0.10949727,  0.90904807],
       [-0.94376106,  0.01902826,  0.64057315],
       [-0.93101185, -0.78644317,  0.60886999],
       [-0.73691806, -0.29873262,  0.97822225]])

查看四分位数：

1 np.random.seed(666)
2 arr = np.random.randn(1000)
3 arr.sort()
4 arr[int(0.25 * len(arr))]
5 arr[int(0.75 * len(arr))]

-0.6786323778244538
0.6879940536373379

唯一值和集合逻辑

NumPy 有一些一维数组的基本的集合运算。其中 np.unique 是非常常用的。

1 names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
2 np.unique(names)
3 ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
4 np.unique(ints)
5 # 纯 Python 实现
6 sorted(set(names))

array(['Bob', 'Joe', 'Will'], dtype='<U4')
array([1, 2, 3, 4])
['Bob', 'Joe', 'Will']

np.in1d 检查两个数组值的关系。

1 values = np.array([6, 0, 0, 3, 2, 5, 6])
2 np.in1d(values, [2, 3, 6])

array([ True, False, False,  True,  True, False,  True])

数组常用的集合运算有：

unique(x)
intersect1d(x, y)
union1d(x, y)
in1d(x, y)
setdiff1d(x, y)
setxor1d(x, y)

数组的文件输入和输出

NumPy 可以用文本或者二进制的方式把数据存储到硬盘，我们一般都选用二进制的方式。

np.save 和 np.load 分别是以二进制存储和加载的函数。

1 arr = np.arange(10)
2 # 持久化
3 np.save('arr_data.npy', arr)
4 # 加载
5 np.load('arr_data.npy')

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

还可以以非压缩或者压缩的格式保存多个 NumPy 数据：

1 # 非压缩
2 np.savez('arr_archive.npz', a=arr, b=arr)
3 # 压缩
4 np.savez_compressed('arr_compressed.npz', a=arr, b=arr)
5 # 加载
6 arch = np.load('arr_archive.npz')
7 arch['b']
8 cmp = np.load('arr_compressed.npz')
9 cmp['a']

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

线性代数

矩阵运算使用的是 dot 函数。

1 x = np.array([[1., 2., 3.], [4., 5., 6.]])
2 y = np.array([[1., 2.], [-1, 0], [0, 1]])
3 x
4 y
5 x.dot(y)
6 np.dot(x, y)  # 等价于 x.dot(y)
7 x @ y  # Python3.5，等价于 x.dot(y)

array([[1., 2., 3.],
       [4., 5., 6.]])
array([[ 1.,  2.],
       [-1.,  0.],
       [ 0.,  1.]])
array([[-1.,  5.],
       [-1., 14.]])
array([[-1.,  5.],
       [-1., 14.]])
array([[-1.,  5.],
       [-1., 14.]])

numpy.linalg 有很多关于矩阵分解（如求逆、行列式等）的函数。

1 from numpy.linalg import inv, qr
2 
3 np.random.seed(666)
4 X = np.random.randn(3, 3)
5 mat = X.T.dot(X)
6 inv(mat)
7 mat.dot(inv(mat))  # 等于单位矩阵
8 q, r = qr(mat)
9 r

array([[ 0.94360937,  0.09940334, -0.46256198],
       [ 0.09940334,  0.70123855, -0.05689685],
       [-0.46256198, -0.05689685,  0.78260277]])
array([[ 1.00000000e+00,  8.64663156e-18, -4.04784612e-17],
       [ 1.27360445e-17,  1.00000000e+00,  6.98841494e-18],
       [-7.26002573e-17, -9.92956304e-18,  1.00000000e+00]])
array([[-1.7499547 ,  0.22916446, -1.66008207],
       [ 0.        , -1.43686954, -0.22584526],
       [ 0.        ,  0.        ,  1.09786224]])

常用的 numpy.linalg 函数：

diag
dot
trace
det
eig
inv
pinv
qr
svd
solve
lstsq

生成伪随机数

numpy.random 有各种生成随机数样本的函数，比原生 Python 随机数生成模块速度快很多。

生成的随机数称为伪随机数，因为这些随机数实际上依赖于 np.random.seed 的值。

1 np.random.seed(666)
2 samples = np.random.normal(size=(4, 4))
3 samples

array([[ 0.82418808,  0.479966  ,  1.17346801,  0.90904807],
       [-0.57172145, -0.10949727,  0.01902826, -0.94376106],
       [ 0.64057315, -0.78644317,  0.60886999, -0.93101185],
       [ 0.97822225, -0.73691806, -0.29873262, -0.46058737]])

可以使用全局随机种子：

1 rng = np.random.RandomState(666)
2 rng.randn(10)

array([ 0.82418808,  0.479966  ,  1.17346801,  0.90904807, -0.57172145,
       -0.10949727,  0.01902826, -0.94376106,  0.64057315, -0.78644317])

常用的随机函数如下：

seed
permutation
shuffle
rand
randint
randn
binomial
normal
beta
chisquare
gamma
uniform

使用 NumPy 实现一个随机游走的例子

1 np.random.seed(666)
2 nsteps = 1000  # 随机游走的步数
3 draws = np.random.randint(0, 2, size=nsteps)  # 生成 0 或 1，一共 nsteps 个点
4 steps = np.where(draws == 0, 1, -1)  # 等于 0 则设为 1，不等于 0 则设为 -1
5 walk = steps.cumsum()  # 累积求和
6 walk.min()
7 walk.max()
8 (np.abs(walk) >= 10).argmax()  # 第一次绝对值超过 10 的索引
9 plt.plot(walk[:100])

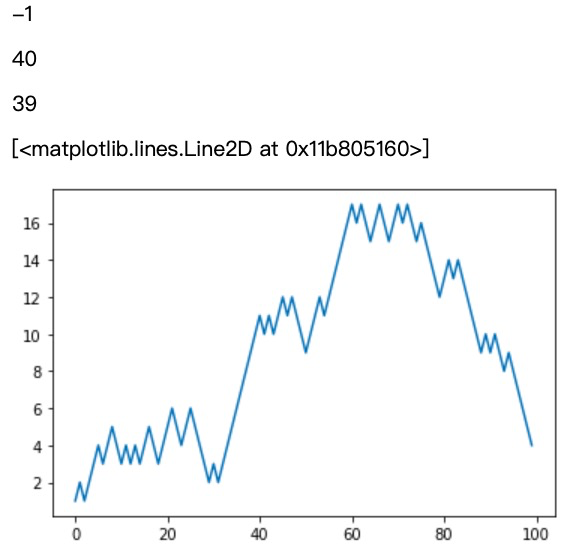
同时模拟多个随机游走

1 np.random.seed(666)
2 nwalks = 5000
3 nsteps = 1000
4 draws = np.random.randint(0, 2, size=(nwalks, nsteps))
5 steps = np.where(draws > 0, 1, -1)
6 walks = steps.cumsum(1)  # 1 表示针对 axis=1
7 walks
8 walks.shape  # 行表示模拟的不同随机游走趋势，列表示不同的步数

array([[ -1,  -2,  -1, ..., -22, -21, -22],
       [  1,   2,   1, ...,  20,  19,  20],
       [  1,   0,  -1, ..., -14, -13, -12],
       ...,
       [ -1,   0,   1, ...,  24,  25,  26],
       [ -1,  -2,  -1, ...,  16,  15,  16],
       [ -1,   0,  -1, ..., -24, -23, -22]])
(5000, 1000)

总结

本文介绍了 NumPy 基本操作。

NumPy 最重要的数据结构是 ndarray。我们熟悉了：

怎么创建 ndarray
ndarray 的数据类型
ndarray 的算术运算
如何使用索引、切片、布尔索引、fancy 索引
数组的转置和轴的变换

围绕着 ndarray，NumPy 还提供了很多函数和方法：

通用函数：实现快速的按元素的运算
面向数组的编程：条件逻辑、数学和统计方法、布尔数组的方法、排序方法、唯一值及集合逻辑
数组的持久化和加载方法
线性代数方面：dot 和 numpy.linalg 包
有关随机数生成的 np.random

最后是一个有关随机游走的简单示例。

通过本文我们主要知道了 NumPy 的核心数据结构 ndarray，以及有关它的各种函数出现的源头都是：

向量化的思想——数值计算尽量别用 for 循环，这样代码看起来简单，性能也好得多。

最后欢迎留言，有不足之处请指正。

参考

《Python for Data Analysis, 2nd Edition》by Wes McKinney

posted on 2019-08-11 21:12 何雨龙阅读(1135) 评论(0) 编辑收藏举报

刷新页面返回顶部