神经网络属于“联结主义”,和统计机器学习的理论基础区别还是很不一样。
以我自己的理解,统计机器学习的理论基于统计学,理论厚度足够强,让人有足够的安全感;而神经网络的理论更侧重于代数,表征能力特别强,不过可解释性欠佳。
这两个属于机器学习的两个不同的流派,偶尔也有相互等价的算法。
本文回顾神经网络最简单的构件:感知器、多层感知器。一些简单的代码实践可以参考:Python 实现感知器的逻辑电路(与门、与非门、或门、异或门)。
感知器
感知器是二类分类的线性分类模型,将实例划分为正负两类的分离超平面(separating hyperplane),属于判别模型。
感知器基于线性阈值单元(Linear Threshold Unit, LTU)构件的。以下是 LTU:
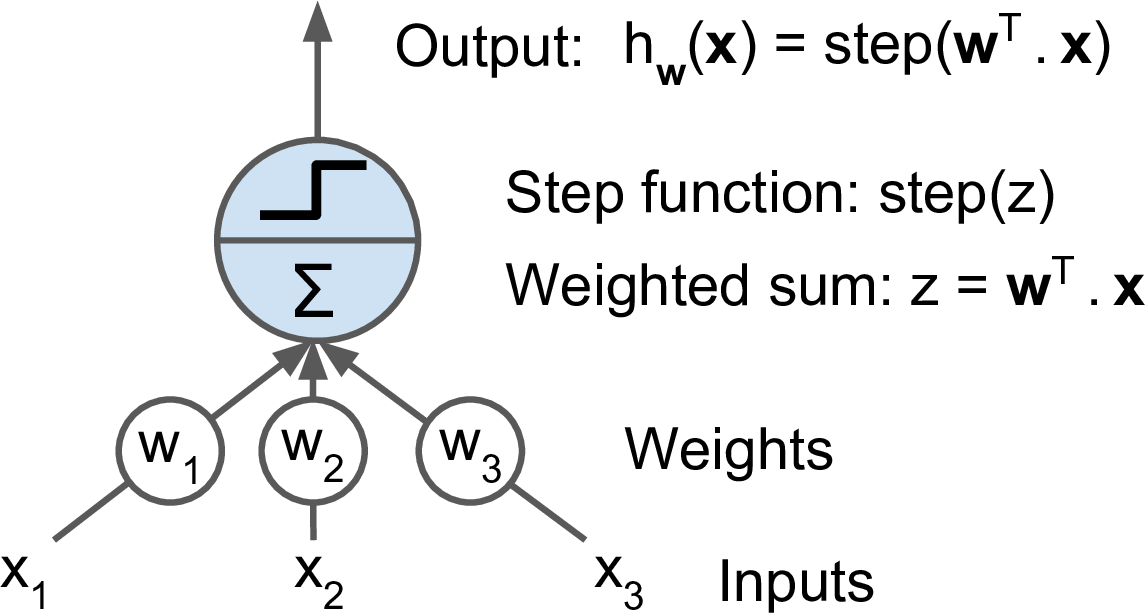
LTU 相当于对输入做一个线性组合,再加一个阶跃函数。
常用的阶跃函数是 Heaviside 和 Sign。
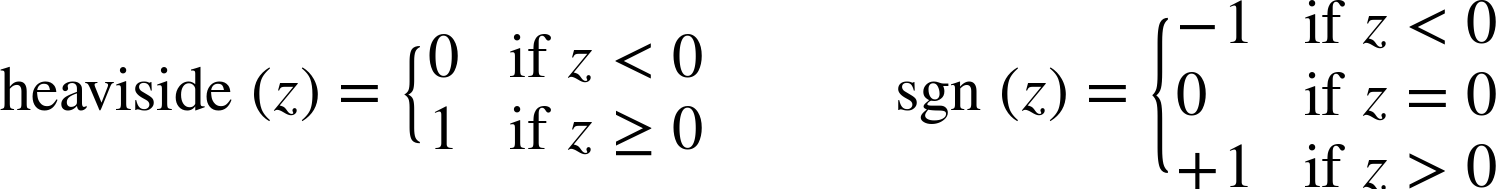
哪怕只有一个 LTU 也可以作为简单的线性二分类器,类似于逻辑回归或者线性 SVM。
感知器就是由一层 LTU 组成。以下是一个多输出分类器。
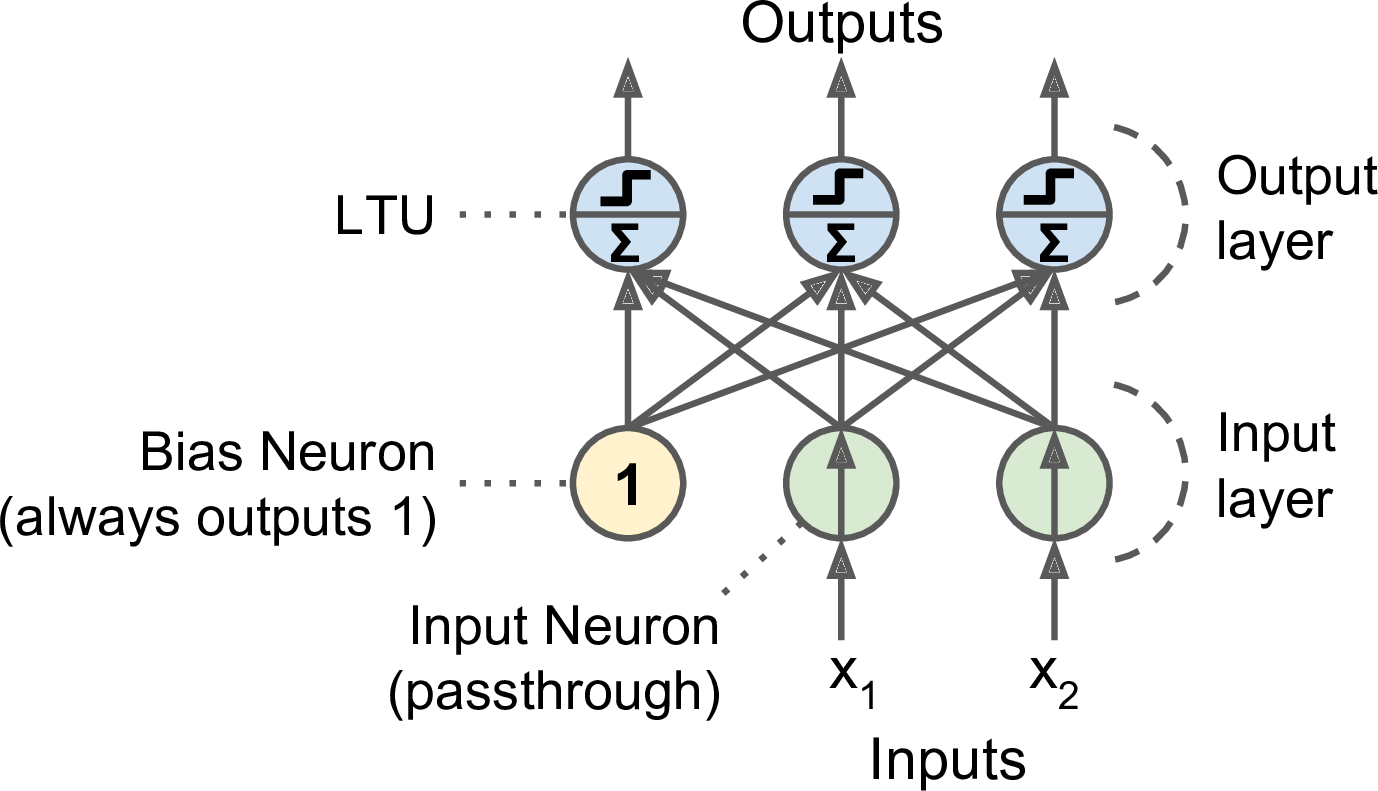
为了求得感知器的权重参数,需要确定一个学习策略,即定义损失函数并将损失函数极小化。有这样几种选择:
1. 误分类点的总数:损失函数不是 w, b 的连续可导函数,不易优化。
2. 误分类点到超平面的总距离:感知器所采用的损失函数。
感知器的损失函数是:
$$-\frac{1}{\left \| w \right \|}\sum_{x_i\in M}y_i(wx_i+b)$$
感知器学习问题转化为上式损失函数的最优化问题,最优化的方法是随机梯度下降法(stochastic gradient decent)。
感知器收敛性:当训练数据集线性可分时,感知器学习算法原始形式是收敛的。
感知器的具体算法分为两种形式:
1. 原始形式
2. 对偶形式:暂不介绍
原始形式算法:
$$w\leftarrow w+\eta y_ix_i$$
$$b\leftarrow b+\eta y_i$$
使用 sklearn 使用感知器算法:
1 import numpy as np 2 from sklearn.datasets import load_iris 3 from sklearn.linear_model import Perceptron 4 5 iris = load_iris() 6 X = iris.data[:, (2, 3)] # petal length, petal width 7 y = (iris.target == 0).astype(np.int) # Iris Setosa? 8 per_clf = Perceptron(random_state=42) 9 per_clf.fit(X, y) 10 11 y_pred = per_clf.predict([[2, 0.5]]) 12 13 print(y_pred)
输入如下:
[1]
与逻辑回归相比,感知器不能输出概率。
多层感知器
MLP 的组成:
- 1 个输入层
- 1 个以上的隐藏层
- 1 个输出层
当隐藏层多于 2 层时,又叫深度神经网络(Deep Neural Network, DNN)。
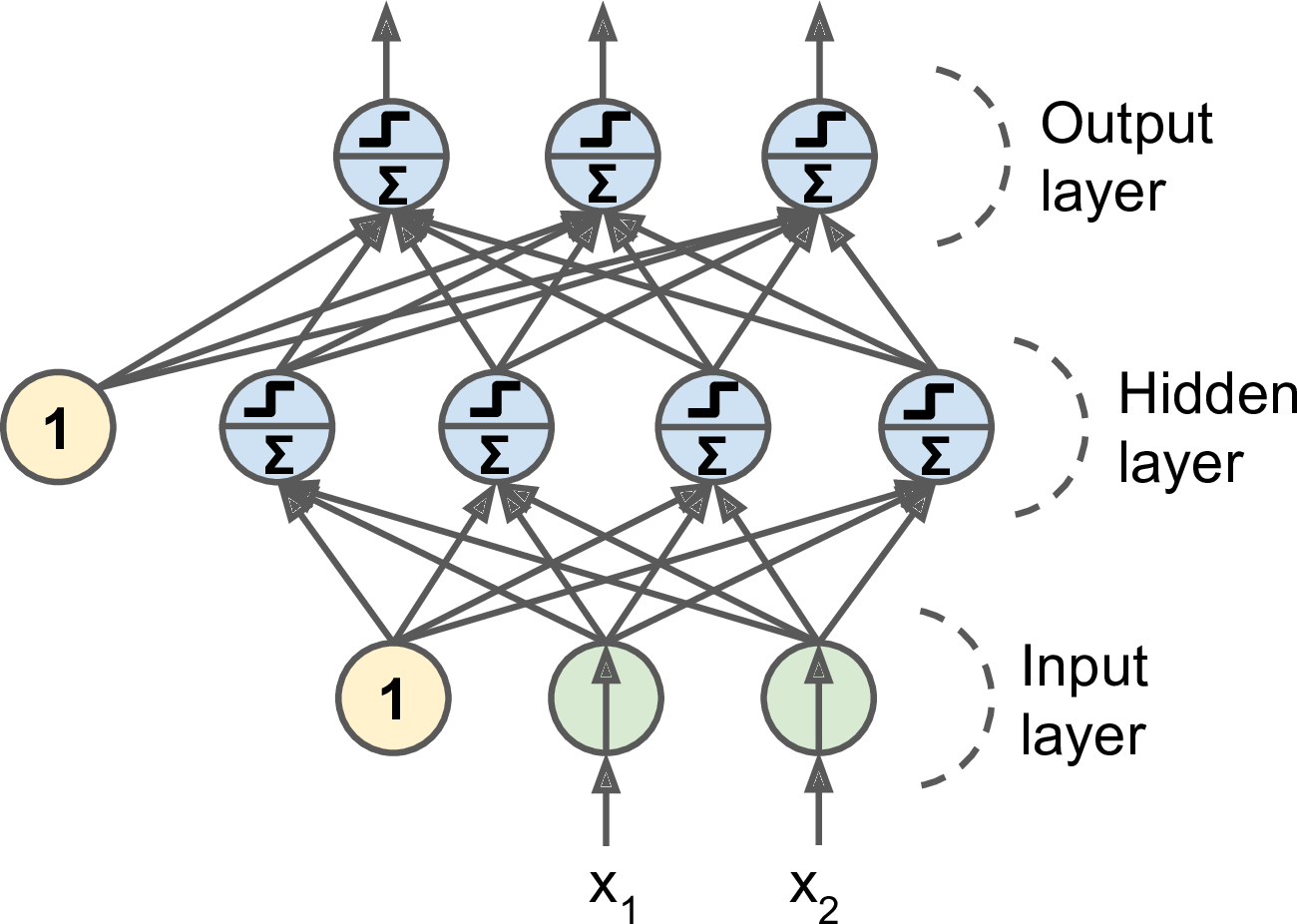
训练 MLP 的算法是后馈训练算法(backpropagation training algorithm)。后馈训练算法也就是使用反向自动求导(reverse-mode autodiff)的梯度下降法。
1. 前馈:在每个连接层计算每个神经元的输出。
2. 计算网络的输出误差,并且计算最后一层的每个神经元对于误差的贡献程度。
3. 继续计算上一层的每个神经元对于误差的贡献程度。
4. 直到算法到达输入层。
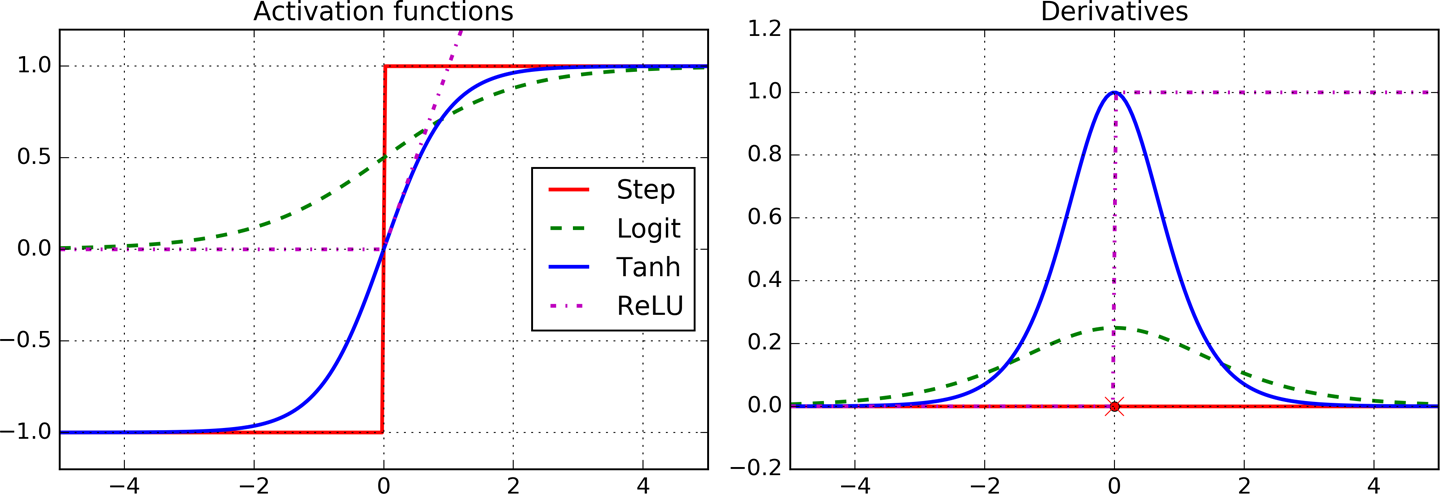
为了很好地实施后馈训练算法,D. E. Rumelhart 对于神经网络架构做了重大的改变:把阶跃函数改为了几率函数(logistic function)$f(z)=\frac{1}{1+e^{-z}}$。因为阶跃函数导数都为 0,无法实施梯度下降;而几率函数处处可导。
除了用几率函数作为激活函数之外,还有:
- 双曲正切函数:tanh (z) = 2σ(2z) – 1。S 形状、连续、可导,不过输出值在 -1 到 1 之间,使得训练开始时神经层输出更加正则化,常常加速收敛。
- ReLU 函数:ReLU (z) = max (0, z)。连续,但是在 z=0 处不可导,可能使梯度下降震荡。但在实际中,ReLU 效果不错,速度也快。此外,由于它没有最大值,可以缓解一些梯度下降的问题。
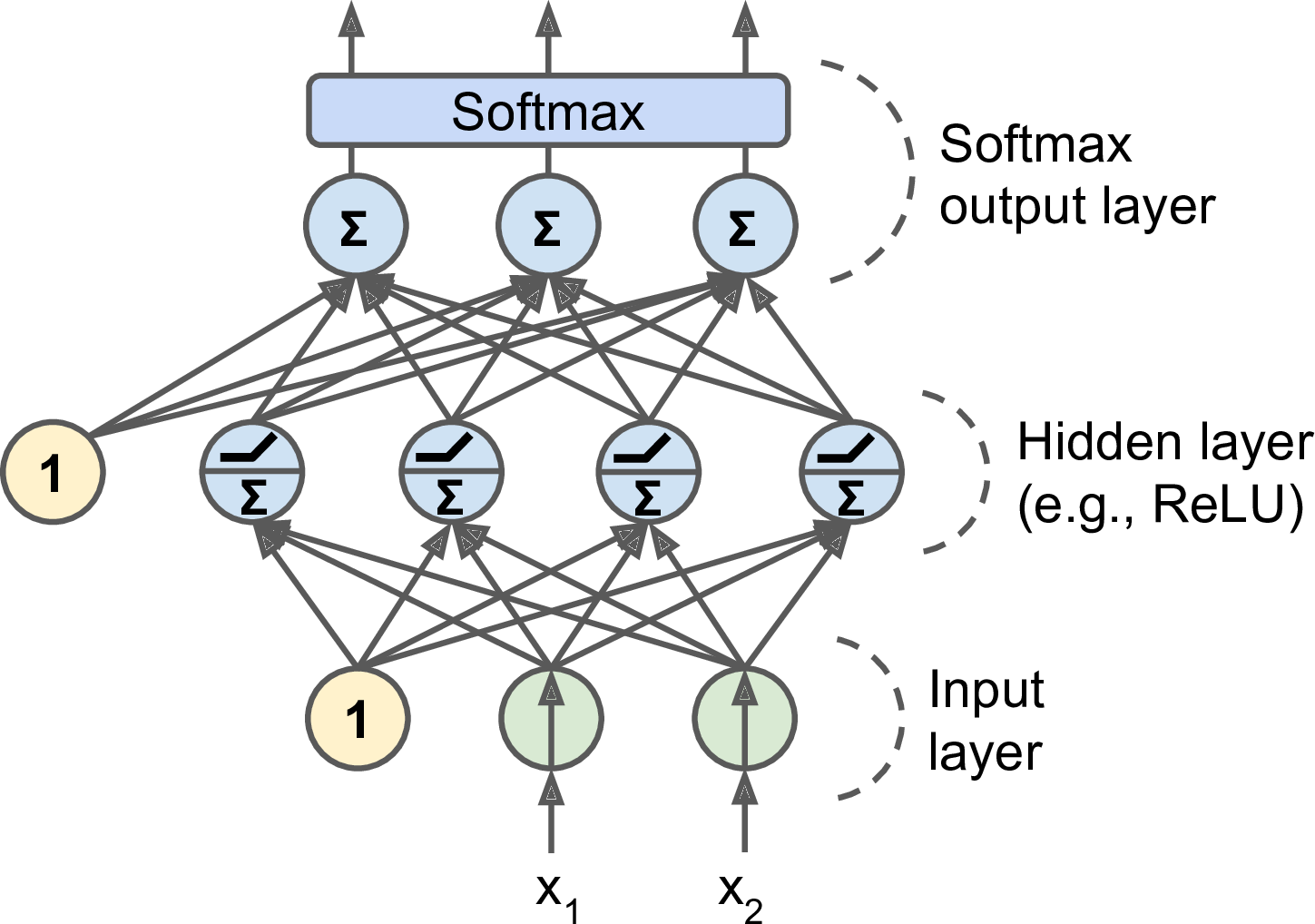
MLP 常常用于分类问题,每个输出对应一个不同的二值类别。如果类别太多了(比如数字图片 0~9),输出层常常用另一个共用的激活函数来代替:Softmax 函数。
参考
- 《Neural networks and deep learning》by Aurélien Géron


 posted on
posted on
