SVD与SVD++
参考自：http://blog.csdn.net/wjmishuai/article/details/71191945
http://www.cnblogs.com/Xnice/p/4522671.html
基于潜在（隐藏）因子的推荐，常采用SVD或改进的SVD++
奇异值分解（SVD）：
考虑CF中最为常见的用户给电影评分的场景，我们需要一个数学模型来模拟用户给电影打分的场景，比如对评分进行预测。
将评分矩阵U看作是两个矩阵的乘积：
其中，uxy 可以看作是user x对电影的隐藏特质y的热衷程度，而iyz可以看作是特质 y 在电影 z中的体现程度。那么上述模型的评分预测公式为：
q 和 p 分别对应了电影和用户在各个隐藏特质上的特征向量。
以上的模型中，用户和电影都体现得无差别，例如某些用户非常挑剔，总是给予很低的评分；或是某部电影拍得奇烂，恶评如潮。为了模拟以上的情况，需要引入 baseline predictor.
其中 μ 为所有评分基准，bi 为电影 i 的评分均值相对μ的偏移，bu 类似。注意，这些均为参数，需要通过训练得到具体数值，不过可以用相应的均值作为初始化时的估计。
模型参数bi,bu,qi,pu通过最优化下面这个目标函数获得：
可以用梯度下降方法或迭代的最小二乘算法求解。在迭代最小二乘算法中，首先固定pu优化qi，然后固定qi优化pu，交替更新。梯度下降方法中参数的更新式子如下（为了简便，把目标函数中的μ+bi+bu+q⊤ipu整体替换为r^ui）：
其中α是更新步长。
SVD++：
某个用户对某个电影进行了评分，那么说明他看过这部电影，那么这样的行为事实上蕴含了一定的信息，因此我们可以这样来理解问题：评分的行为从侧面反映了用户的喜好，可以将这样的反映通过隐式参数的形式体现在模型中，从而得到一个更为精细的模型，便是 SVD++.
其中 I(u) 为该用户所评价过的所有电影的集合，yj为隐藏的“评价了电影 j”反映出的个人喜好偏置。收缩因子取集合大小的根号是一个经验公式，并没有理论依据。
模型参数bi,bu,qi,pu,yj通过最优化下面这个目标函数获得：
与SVD方法类似，可以通过梯度下降算法进行求解。
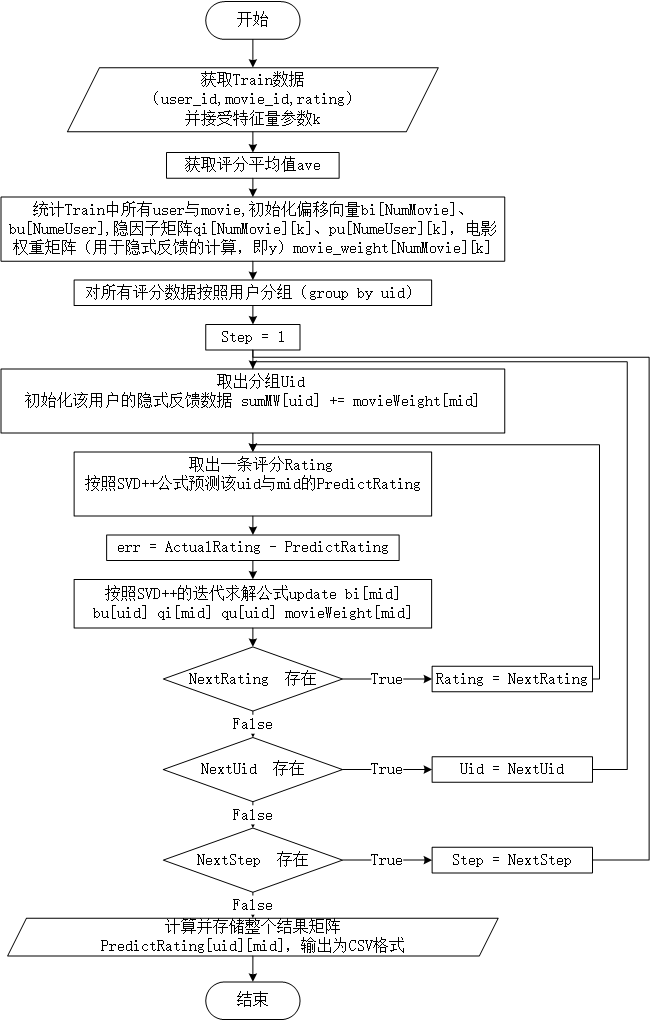
使用用户的历史评价数据作为隐式反馈，算法流程图如下：
