隐马尔科夫模型

马尔科夫过程

马尔科夫过程可以看做是一个自动机，以一定的概率在各个状态之间跳转。

考虑一个系统，在每个时刻都可能处于N个状态中的一个，N个状态集合是 {S₁,S₂,S₃,...S_N}。我们现在用q₁,q₂,q₃,…q_n来表示系统在t=1,2,3,…n时刻下的状态。在t=1时，系统所在的状态q取决于一个初始概率分布PI，PI(S_N)表示t=1时系统状态为S_N的概率。

马尔科夫模型有两个假设：

1. 系统在时刻t的状态只与时刻t-1处的状态相关；（也称为无后效性）

2. 状态转移概率与时间无关；（也称为齐次性或时齐性）

第一条具体可以用如下公式表示：

P(q_t=S_j|q_t-1=S_i,q_t-2=S_k,…)= P(q_t=S_j|q_t-1=S_i)

其中，t为大于1的任意数值，S_k为任意状态

第二个假设则可以用如下公式表示：

P(q_t=S_j|q_t-1=S_i)= P(q_k=S_j|q_k-1=S_i)

其中，k为任意时刻。

隐马尔科夫模型由初始状态向量S、状态转移概率矩阵A和观测概率矩阵B决定，S和A决定状态序列，B决定观测序列，因此，隐马尔科夫模型λ可以用三元组符号表示，即

　　　　λ=(A,B,S)

A,B,S称为隐马尔科夫模型的三要素。

隐马尔科夫可以解决的三个问题

(1)概率计算问题：给定模型λ=(A,B,S)和观测序列O=(o₁,o₂,...,o_r),计算在模型λ下观测序列O出现的概率p(O|λ)

①直接计算法

如果穷尽所有的状态组合，即S₁S₁...S₁, S₁S₁...S₂, S₁S₁...S₃, ..., S₃S₃...S₃。这样的话t₁时刻有N个状态，t₂时刻有N个状态...t_T时刻有N个状态，这样的话一共有N*N*...*N= N^T种组合，时间复杂度为O(N^T),计算时，就会出现“指数爆炸”，当T很大时，简直无法计算这个值。为解决这一问题，Baum提出了前向算法。

②前向算法

归纳过程

首先引入前向变量α_t(i):在时间t时刻，HMM输出序列为O₁O₂...O_T,在第t时刻位于状态s_i的概率。

当T=1时，输出序列为O₁,此时计算概率为P(O₁|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₁得概率为b₁(O₁),从状态2发出观察值O₁得概率为b₂(O₁),从状态3发出观察值O₁得概率为b₃(O₁)。因此可以算出

P(O₁|μ）= π₁*b₁(O₁)+π₂*b₂(O₁) + π₃*b₃(O₁)= α₁(1) + α₁(2) + α₁(3)

当T=2时，输出序列为O₁O₂,此时计算概率为P(O₁O₂|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₂得概率为b₁(O₂),从状态2发出观察值O₂得概率为b₂(O₂),从状态3发出观察值O₂得概率为b₃(O₂)。

要是从状态1发出观察值O₂，可能从第一时刻的1、2或3状态装换过来，要是从状态1转换过来，概率为α₁(1)*a₁₁*b₁(O₂),要是从状态2转换过来，概率为α₁(2)*a₂₁*b₁(O₂),要是从状态3转换过来，概率为α₁(3)*a₃₁*b₁(O₂),因此

P(O₁O_₂,q₂₌s₁|μ）= α₁(1)*a₁₁*b₁(O₂) + α₁(2)*a₂₁*b₁(O₂) + α₁(3)*a₃₁*b₁(O₂)=α₂(1)

同理：P(O₁O_₂_,q₂₌s₁|μ）= α₁(1)*a₁₂*b₂(O₂) + α₁(2)*a₂₂*b₂(O₂) + α₁(3)*a₃₂*b₂(O₂)=α₂(2)

P(O₁O_₂_,q₂₌s₁|μ）= α₁(1)*a₁₃*b₁(O₂) + α₁(2)*a₂₃*b₃(O₂) + α₁(3)*a₃₃*b₃(O₂)=α₂(3)

所以：P(O₁O_₂|μ）=P(O₁O_₂,q₂₌s₁|μ）+ P(O₁O_₂_,q₂₌s₁|μ）+ P(O₁O_₂_,q₂₌s₁|μ）

=α₂(1) + α₂(2) + α₂(3)

以此类推。。。

前向算法

step1 初始化：α₁(i) = π_i*b_i(O₁), 1≤i≤N

step2 归纳计算:

step3 终结：

P(O|μ）=

时间复杂度

计算某时刻的某个状态的前向变量需要看前一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

程序例证

前向算法计算P(O|M)：

step1：α₁(1) =π₁*b₁(red)=0.2*0.5=0.1 α₁(2)=π₂*b₂(red)==0.4*0.4= 0.16 α₁(3)=π₃*b₃(red)==0.4*0.7=0.21

step2：α₂(1)=α₁(1)*a₁₁*b₁(white) + α₁(2)*a₂₁*b₁(white) + α₁(3)*a₃₁*b₁(white)

...

step3:P(O|M) = α₃(1)+α₃(2)+α₃(3)程序代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float alpha[4][3];
        int i,j,k, count = 1;
        //output list
        int list[4] = {0,1,0,1};
        //step1:Initialization
        alpha[0][0] = 0.2 * 0.5;
        alpha[0][1] = 0.4 * 0.4;
        alpha[0][2] = 0.4 * 0.7;
        //step2:iteration
        for (i=1; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                alpha[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   alpha[i][j] += alpha[i-1][k] * a[k][j] * b[j][list[count]];
                }
            }
            count += 1;
        }
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("a[%d][%d]=%f\n",i+1,j+1,alpha[i][j]);
            }
        }
       //step3:end
       printf("Forward:%f\n", alpha[3][0]+alpha[3][1]+alpha[3][2]);
       return 0;
}

③后向算法

对于HMM的评估问题，利用动态规划可以用前向算法，从前到后算出前向变量；也可以采用后向算法，从后到前算出后向变量。

先介绍后向变量β_t(i):给定模型μ=（A,B,π），并且在时间 时刻t 状态为s_i的前提下，输出序列为O_t+1O_t+2...O_T的概率，即

β_t(i)=P(O_t+1O_t+2...O_T|q_t=s_i,μ)

归纳过程

假设仍然有3个状态

当t=T时，按照定义：时间t 状态q_T输出为O_T+1......的概率，从T+1开始的输出是不存在的（因为T时刻是终止终止状态），即T之后是空，是个必然事件，因此β_t(i)=1,1≤1≤N

当t=T-1时，

β_T-1(i)=P(O_T|q_T-1=s_i,μ) = a_i1*b₁（O_T)*β_T(1) + a_i2*b₂（O_T)*β_T(2) + a_i3*b₃（O_T)*β_T(3)

......

当t=1时，

β₁(1)=P(O₂O_3...O_T|q₂=s₁,μ) = a₁₁*b₁（O₂)*β₂(1) + a₁₂*b₂（O₂)*β₂(2) + a₁₃*b₃（O₂)*β₂(3)

β₁(2)=P(O₂O_3...O_T|q₂=s₁,μ) = a₂₁*b₁（O₂)*β₂(1) + a₂₂*b₂（O₂)*β₂(2) + a₂₃*b₃（O₂)*β₂(3)

β₁(3)=P(O₂O_3...O_T|q₂=s₁,μ) = a₃₁*b₁（O₂)*β₂(1) + a₃₂*b₂（O₂)*β₂(2) + a₃₃*b₃（O₂)*β₂(3)

P(O₁O₂...O_T|μ) =

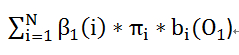
后向算法

step1 初始化：β_T(i)=1, 1≤1≤N

step2 归纳计算：

1≤t≤T-1, 1≤i≤N

step3 求终结和：

P(O|μ）=

时间复杂度

计算某时刻在某个状态下的后向变量需要看后一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

程序例证

后向算法

计算P(O|M)：

step1：β₄(1) = 1 β₄(2) = 1 β₄(3) = 1

step2：β₃(1) = β₄(1)*a₁₁*b₁(white) + β₄(2)*a₁₂*b₂(white) + β₄(3)*a₁₃*b₃(white)

...

step3:P(O|M) = π₁*β₁(1)*b₁(O₁) + π₂*β₁(2)*b₂(O₁) + π₃*β₁(3)*b₃(O₁)

程序代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float result[4][3];
        int list[4] = {0,1,0,1};
        result[3][0] = 1;
        result[3][1] = 1;
        result[3][2] = 1;
        int i,j,k, count = 3;
        for (i=2; i>=0; i--)
        {
            for(j=0; j<=2; j++)
            {
                result[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   result[i][j] += result[i+1][k] * a[j][k] * b[k][list[count]];
                }
            }
            count -= 1;
        }
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("b[%d][%d] = %f\n",i+1,j+1,result[i][j]);

            }
        }
        printf("backward:%f\n", result[0][0]*0.2*0.5+result[0][1]*0.4*0.4+result[0][2]*0.4*0.7);
        return 0;
}

④前向后向算法

重新回顾：

前向变量α_t(i):在时刻t,在已知模型μ=（A,B,π）的条件下，状态处于s_i,输出序列为O₁0₂...O_t,前向变量为α_t(i)

后向变量β_t(i):在时刻t,在已知模型μ=（A,B,π）和状态处于s_i的条件下，输出序列为O_t+1O_t+2...O_T,后向变量为β_t(i)

公式推导：

P(O,q_t=s_i|μ） = P(O₁O₂...O_T, q_t=s_i|μ）

=P(O₁O₂...O_t,q_t=si,O_t+1O_t+2...O_T|μ)

=P(O₁O₂...O_t,q_t=si|μ) * P(O_t+1O_t+2...O_T|O₁O₂...O_t,q_t=si,μ)

=P(O₁O₂...O_t,q_t=si|μ) * P(O_t+1O_t+2...O_T|q_t=si,μ)

=α_t(i) * β_t(i)

P(O|μ）=

案例分析：

分析：

P(q₄=s₃|O,M) = P(q₄=s₃, O|M)/P(O|M)

= P(O,q₄=s₃|M)/P(O|M)

= α₄(3) * β₄(3)/

程序代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float result_b[8][3];
        float result_f[8][3];
        float result, result_t;
        int list[8] = {0,1,0,0,1,0,1,1};
        result_b[7][0] = 1;
        result_b[7][1] = 1;
        result_b[7][2] = 1;
        result_f[0][0] = 0.2 * 0.5;
        result_f[0][1] = 0.4 * 0.4;
        result_f[0][2] = 0.4 * 0.7;
        //Backward
        int i,j,k, count = 7;
        for (i=6; i>=0; i--)
        {
            for(j=0; j<=2; j++)
            {
                result_b[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   result_b[i][j] += result_b[i+1][k] * a[j][k] * b[k][list[count]];
                }
            }
            count -= 1;
        }
       for (i=0; i<=7; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("b[%d][%d]= %f\n",i+1,j+1, result_b[i][j]);

            }
        }
        printf("Backward:%f\n", result_b[0][0]*0.2*0.5+result_b[0][1]*0.4*0.4+result_b[0][2]*0.4*0.7);
        //Forward
        count = 1;
        for (i=1; i<=7; i++)
        {
            for(j=0; j<=2; j++)
            {
                result_f[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                    result_f[i][j] += result_f[i-1][k] * a[k][j] * b[j][list[count]];
                }
            }
            count += 1;
        }
        for (i=0; i<=7; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("a[%d][%d]= %f\n", i+1, j+1, result_f[i][j]);
            }
        }
        result = result_f[7][0] + result_f[7][1] + result_f[7][2];
        printf("Forward: %f\n", result);
        
        result_t = 0;
        for (i=0; i<=2; i++)
        {
            result_t += result_f[3][i] * result_b[3][i];
        }
        printf("Result:%f\n", result_f[3][2]*result_b[3][2]/result_t);

        return 0;
}

(2)学习模型：已知观测序列O=(o₁,o₂,...,o_r)，估计模型λ=(A,B,S)的参数，使得在该模型下观测序列概率p(O|λ)最大，即用极大似然估计的方法估计参数

隐马尔可夫模型的学习问题：给定一个输出序列O=O₁O₂...O_T,如何调节模型μ=(A,B,π）的参数，使得P(O|M)最大。

最大似然估计是一种解决方法，如果产生的状态序列为Q=q₁q₂...q_T,根据最大似然估计，可以通过以下公式推算：

π_i‘ = δ（q₁,s_i)

a_ij' = Q中从状态q_i转移到q_j的次数/Q中从状态q_i转移到另一状态（包括q_j)的次数

b_j(k)' = Q中从状态q_j发出符号V_k的次数/ Q中到达状态q_j的次数

δ（x,y)为克罗奈克函数，当x=y时，δ（x,y)=1；否则，δ（x,y)=0

但是注意，在实际中，状态Q=q₁q₂...q_T是观察不到的（隐变量），因此上述的这种求法是有问题的。幸好希望最大化，可以用于含有隐变量的统计模型的参数最大似然估计。基本思想是初始时，随机的给模型参数赋值，但是要遵循模型对参数的限制，例如，从一个状态发出的所有状态转移概率之和为1，得到模型μ₀。然后根据μ₀中的具体值，带入下式，可以得到u₁.依次往下迭代，直到收敛于最大似然估计值。这种迭代爬山算法可以局部使P(O|μ）最大。称为Baum-Welch算法或前向后向算法。

给定HMM的参数μ和观察序列O=O₁O₂...O_T,在时间t位于状态s_i,在时间t+1位于状态s_j的概率为ξ_t(i,j)=P(q_t=s_i,q_t+1=s_j|O,μ），公式推导如下：

................(1)

给定HMM μ 和序列O=O₁O₂...O_T，在时间t位于状态si的概率为：.........(2)

这样求μ的参数估计重新改写：

π_i‘ = r₁(i) ...........(3)

a_ij' = Q中从状态q_i转移到q_j的次数/Q中从状态q_i转移到另一状态（包括q_j)的次数

= ..........(4)

b_j(k)' = Q中从状态q_j发出符号V_k的次数/ Q中到达状态q_j的次数

= ..............(5)

前向后项算法：

step1 初始化：随机地给定参数 π_i, a_ij, b_j(k),使其满足条件：

由此得到μ₀，令i=0

step2 EM计算：

E步骤：根据（1）（2）式计算期望ξ_t(i,j) 和 r_t(i)

M步骤：根据期望ξ_t(i,j) 和 r_t(i),带入（3）（4）（5）重新得到π_i, a_ij, b_j(k)，得到μ_i+1

step3 循环计算： i = i+1, 直到π_i, a_ij, b_j(k)收敛

(3)预测问题：已知模型λ=(A,B,S)和观测序列O=(o₁,o₂,...,o_r)，求给定观测序列条件概率p(O|λ)最大的状态序列。即给定观测序列，求最优可能的对应的状态序列。

一种想法是求出每个状态的概率r_t(i)最大(r_t(i)=P(qt=si,O|μ）)，记q'_t(i)=arg_Qmax(r_t(i))，但是这样做，忽略了状态之间的关系，很可能两个状态之间的概率为0，即a_{q't(i)q't+1(i)}=0,这样求得的“最优”状态序列是不合法的。

为防止状态之间转移概率为0（断续问题），换一种思路，不是求单个状态求得最大值，而是求得整个状态序列最大值，即求

Q'= arg_QmaxP(Q|O,μ）

此时用维特比算法，先定义下维特比变量δt(i):在时间t，HMM沿着一条路径到达状态si，并输出观察序列O=O₁O₂...O_t的最大概率:

　 δ_t(i)=max P(q₁q₂...q_t=s_i,O₁O₂...O_t|μ)

t t+1

上图中，对于从t时刻三个到 t+1时刻的状态1，到底取状态1,2还是3，不是看单独状态1,2还是3的概率，而是看在状态1,2,3各自的维特比变量值乘以相应的状态转换概率，从中选出最大值，假设2时最大，那么记下t+1时刻状态1之前的路径是t时刻的状态2，以此类推。

δ_t(i)的递归关系式: δ_t+1(i)=max_j δ_t(j)*a_ji*b_i(O_t+1),为了记忆路径，定义路径变量ψ_t(i)，记录该路径上的状态s_i的前一个状态。

维特比算法

step1 初始化：

δ_t(i) = π_i*b_i(O₁), 1≤i≤N

ψ_t(i) = 0

step2 归纳计算：

　　　　 δ_t(i)=max_1≤j≤N δ_t-1(j)*a_ji*b_i(O_t),2≤t≤T;1≤i≤N

记忆路径 ψ_t(i) = arg [max_1≤j≤Nδ_t-1(j)*a_ji*b_i(O_t)]

step3 终结:

Q_T' = arg max_1≤i≤N[δ_T(i)]

P'(Q_T') = max_1≤i≤N[δ_T(i)]

　　 step4 路径回溯:

q_t'=ψ_t+1(q_t+1') , t=T-1,T-2...1

时间复杂度

计算某时刻的某个状态的前向变量需要比较前一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

程序例证

step1 初始化：δ₁(1) = 0.2*0.5=0.1 ，δ₁(2) = 0.4*0.4=0.16， δ₁(3) = 0.4*0.7=0.21

step2 归纳计算：δ₂(1) =max[0.1*0.5,0.16*0.3,0.21*0.2]*0.6

...

step3 终结：最佳路径是δ₄(1)δ₄(2)δ₄(3)最大的一个对应的状态

step4 回溯：从最后一个状态往回返

程序代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float result[4][3];
        int list[4] = {0,1,0,1};
        int max[4][3];
        float tmp;
        //step1:Initialization
        result[0][0] = 0.2*0.5;
        result[0][1] = 0.4*0.4;
        result[0][2] = 0.4*0.7;
        
        int i,j,k, count = 1, max_node;
        float max_v;
        //step2:归纳运算
        for (i=1; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                tmp = result[i-1][0] * a[0][j] * b[j][list[count]];
                max[i][j] = 0;
                for(k=1; k<=2; k++)
                {
                    if(result[i-1][k] * a[k][j] * b[j][list[count]] > tmp)
                    {
                        tmp = result[i-1][k] * a[k][j]* b[j][list[count]];
                        max[i][j] = k;
                    }
                   result[i][j] = tmp;
                }
                max_v = result[3][0];
                max_node = 0;
                for (k=1; k<=2; k++)
                {
                    if(result[3][k] > max_v)
                    {
                        max_v = result[3][k];
                        max_node = k;
                    }
                }
            }
            count += 1;
        }
        //step3:终结
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("%d %d     %f\n",i+1,j+1,result[i][j]);

            }
        }
        printf("Pmax=%f\n", max_v);
        printf("step4:%d   \n", max_node+1);
        //step4:回溯
        for(k=3; k>=1; k--)
        {
            printf("step%d:%d  \n",k, max[k][max_node]+1);
            max_node = max[k][max_node];
        }
        return 0;
    }

转自http://www.cnblogs.com/kaituorensheng/archive/2012/12/01/2797230.html

posted @ 2017-05-13 16:07 nolonely 阅读(231) 评论(0) 编辑收藏举报

刷新页面返回顶部

nolonely

很多时候不是我们做不好，而是没有竭尽全力......

隐马尔科夫模型

马尔科夫过程

维特比算法

时间复杂度

程序例证