并查集(Java实现)
(最好在电脑下浏览本篇博客...手机上看代码不方便)
当时学的时候看的一本印度的数据结构书(好像是..有点忘了..反正跟同学们看的都不一样...)...里面把本文提到的所有情况都提到了,我这里只是重复实现,再加上一些个人的理解的图解,最后附上两道并查集的题来帮助理解.
并查集:基本
介绍并查集-> 并查集是一种数据结构, 常用于描述集合,经常用于解决此类问题:某个元素是否属于某个集合,或者 某个元素 和 另一个元素是否同属于一个集合
思路
数组里存的数字代表所属的集合。比如arr[4]==1;代表4是第一组。如果arr[7]==1,代表7也是第一组。既然 arr[4] == arr[7] == 1 ,那么说明4 和 7同属于一个集合,
例子
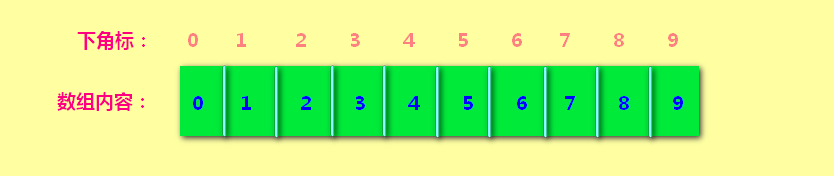
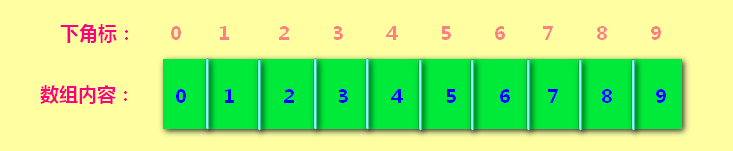
先初始化一个数组。初始时数组内的值与数组的下角标一致。即每个数字都自成立一个小组。
0属于第0个小组(集合),1属于第1个小组(集合),2属于第2个小组(集合)..........
接下来让几个数字进行合并操作,就是组队的过程(合并集合)。合并函数unionElements()介绍:
初始情况如下:
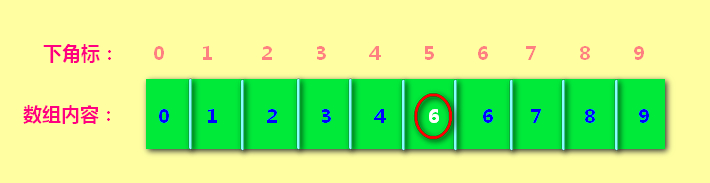
让 5和6进行组队。5里的值就变为6了。含义就是:5放弃了第5小组,加入到了第6小组。5和6属于第6小组。

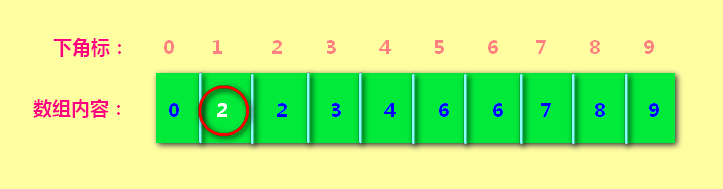
接下来 让1 和2 进行组队。1的下角标就变为2了。含义就是:1和2都属于第2小组。
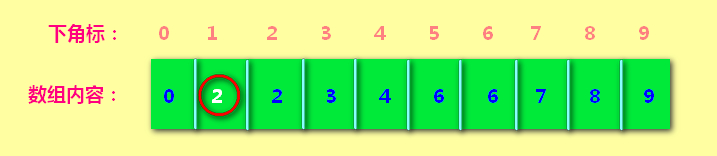
接下来让 2 3进行组队:2想和3进行组队,2就带着原先的所有队友,加入到了3所在的队伍。看下面arr[1] == arr[2]==arr[3]==3,意思就是1 2 3 都属于第3小组。

接下来 1 和 4 进行组队:1就带着原先所有的队友一起加入到4所在的队伍中了。看下面arr[1] == arr[2]==arr[3]==arr[4]==4,意思就是1 2 3 4都属于第4小组。
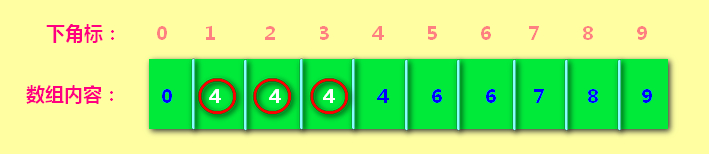
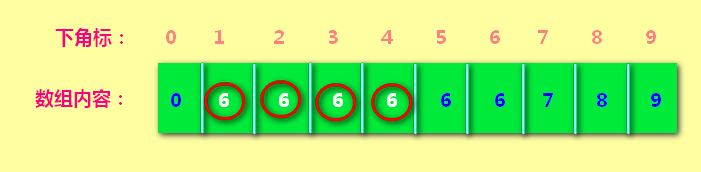
接下来1 和 5进行组队:1就带着原先所有的队友一起加入到5所在的队伍中。5在哪个队伍呢? 因为arr[5]==6,所以5在第6小组。1就带着所有队友进入了小组6。
看下面arr[1] == arr[2]==arr[3]==arr[4]==arr[5]==arr[6]==6,意思就是1 2 3 4 5 6都属于第6小组。
将这个例子的并查集用树形表示来,如下图所示:
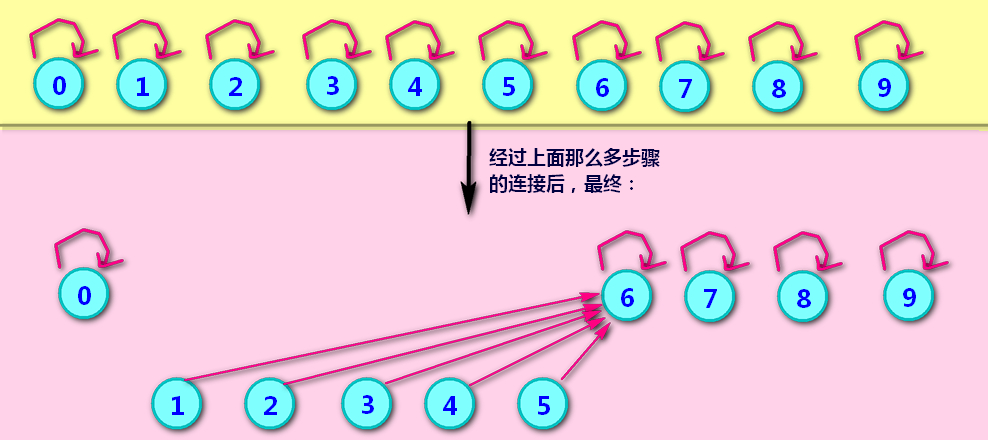
find()函数介绍:怎么求出4属于哪个集合呢,调用find(4)就好了。find(4)返回的结果是什么呢,其实就是arr[4],也就是6,表示4属于第6小组。
isConnected函数介绍:
判断1和6是不是队友(1 和 6 是不是属于同一个集合):arr[1]==arr[6]可知,是队友(属于同一个集合)
判断1和8是不是队友(1 和 8 是不是属于同一个集合):arr[1] != arr[8]可知,不是队友(不属于同一个集合)
代码
/**
* 数组实现并查集,元素内数字代表集合号
*/
public class UnionFind {
/**
* 数组,表示并查集所有元素
*/
private int[] id;
/**
* 并查集的元素个数
*/
private int size;
/**
* 构造一个新的并查集
*
* @param size 初始大小
*/
public UnionFind(int size) {
//初始化个数
this.size = size;
//初始化数组,每个并查集都指向自己
id = new int[size];
for (int i = 0; i < size; i++) {
id[i] = i;
}
}
/**
* 查看元素所属于哪个集合
*
* @param element 要查看的元素
* @return element元素所在的集合
*/
private int find(int element) {
return id[element];
}
/**
* 判断两个元素是否同属于一个集合
*
* @param firstElement 第一个元素
* @param secondElement 第二个元素
* @return <code>boolean</code> 如果是则返回true。
*/
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
/**
* 合并两个元素所在的集合,也就是连接两个元素
*
* @param firstElement 第一个元素
* @param secondElement 第二个元素
*/
public void unionElements(int firstElement, int secondElement) {
//找出firstElement所在的集合
int firstUnion = find(firstElement);
//找出secondElement所在的集合
int secondUnion = find(secondElement);
//如果这两个不是同一个集合,那么合并。
if (firstUnion != secondUnion) {
//遍历数组,使原来的firstUnion、secondUnion合并为secondUnion
for (int i = 0; i < this.size; i++) {
if (id[i] == firstUnion) {
id[i] = secondUnion;
}
}
}
}
/**
* 本并查集使用数组实现,为了更直观地看清内部数据,采用打印数组
*/
private void printArr() {
for (int id : this.id) {
System.out.print(id + "\t");
}
System.out.println();
}
public static void main(String[] args) {
int n = 10;
UnionFind union = new UnionFind(n);
System.out.println("初始:");
union.printArr();
System.out.println("连接了5 6");
union.unionElements(5, 6);
union.printArr();
System.out.println("连接了1 2");
union.unionElements(1, 2);
union.printArr();
System.out.println("连接了2 3");
union.unionElements(2, 3);
union.printArr();
System.out.println("连接了1 4");
union.unionElements(1, 4);
union.printArr();
System.out.println("连接了1 5");
union.unionElements(1, 5);
union.printArr();
System.out.println("1 6 是否连接:" + union.isConnected(1, 6));
System.out.println("1 8 是否连接:" + union.isConnected(1, 8));
}
}
并查集:快速Union,慢Find
上面基本的并查集中,数组里存的内容就是自己所在的小组号,或者可以理解为当前小组的队长号。
上面情况的最后一张图片中。元素1和元素5组队,那么就需要元素1所在队伍的所有成员都把自己的小组号改为新的小组号。伪代码如下:
for (int i = 0; i < 数组size; i++) {
if (是否和元素1同属于队伍4) {
id[i] = secondUnion;//改为新的队伍号
}
}
这样的合并操作太低效了,合并一次就O(n)。所以采用快速Union方式。
思路
原先的数组中存的是小组号(或者队长的编号),而现在数组中存的是自己的‘大哥’的编号。(应该说是父亲结点,和父亲数组,但为了更形象,还是叫‘大哥’更好理解)。
每个元素都可以去认一个大哥去保护自己,避免被欺负。只能认一个大哥...不能认多个
例子
初始情况如下:每个元素里的内容就是自己的下角标(编号)。表示自己就是自己大哥,表示很自由,不从属于任何人。如下图所示
连接5 6 : 后来5号总是受欺负,认6号为大哥,自己的内容就变为6了。如下图所示
连接1 2:后来1号发现自己单着也不行,认2号为大哥,自己的内容就变为2了。如下图所示
连接2 3:后来2号发现自己能力有限,就投奔了3号。
解读一下数组内的含义:arr[1]==2,表示元素1的大哥是2号;arr[2]==3,表示元素2的大哥是3号。所以元素1的老大哥其实是3号。

连接1和4:1号想和4号成为一个小组,怎么办呢?只需要让自己的‘最终老大哥’加入到4号所在的小组就行了。所以1号就撮合自己的‘最终老大’3号,让3号认4号为大哥。(4号是什么来头呢?4号是4号的‘最终老大’,4号自己就是自己的最终老大)。从此1 2 3 4这些元素都是一家子了。

上面这个情况其实用树形结构表示就更加形象了:
连接1 和 4就是把1所在的根指向4。

连接1 5 : 1号想和5号成为一个小组,怎么办呢?只需要让自己的‘最终老大哥’加入到5号所在的小组就行了。所以1号就撮合自己的‘最终老大’4号,让4号认6号为大哥。(6号是什么来头呢?6号是5号的‘最终老大’)。如下图所示。从此1 2 3 4 5 6这些元素都是一家子了。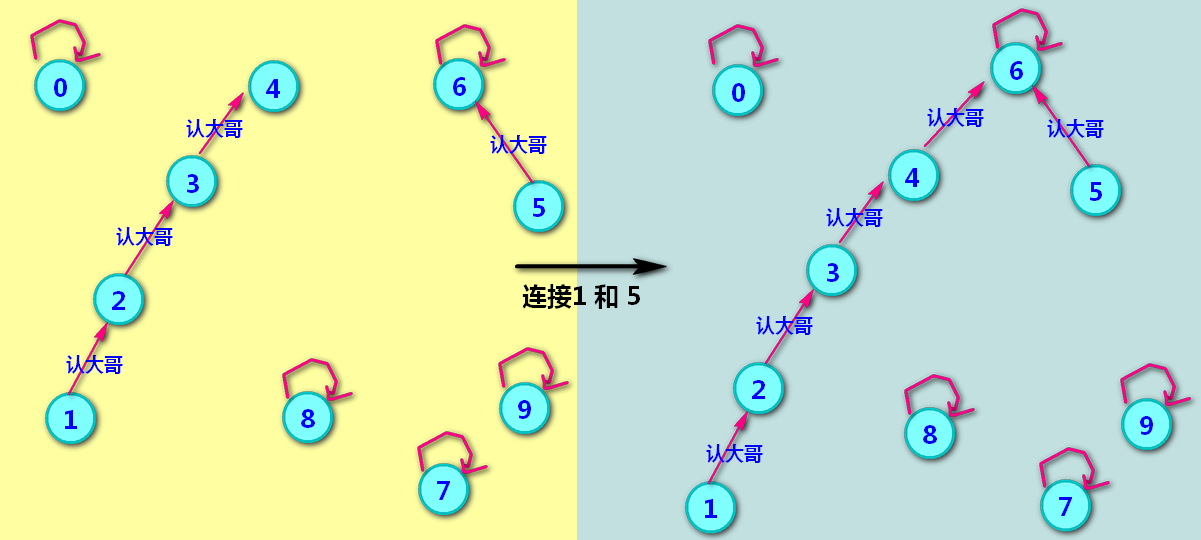
find()函数介绍:find函数就是找大哥的函数。怎么求出4属于哪个集合呢,调用find(1)就好了。find(1)返回的结果是什么呢,其实就是1的‘最终大哥’ 元素4。详细过程见代码。
isConnected函数介绍:
判断1和6是不是队友(1 和 6 是不是属于同一个集合):find(1) 是否等于 find(6),也就是 判断俩元素是否是同一个‘最终大哥’
判断1和8是不是队友(1 和 8 是不是属于同一个集合):find(1) 是否等于 find(8),也就是 判断俩元素是否是同一个‘最终大哥’
代码
/**
* 数组模拟树,实现并查集。数组内的元素表示父亲的下角表,相当于指针。
*/
public class UnionFind {
private int[] parent;
private int size;
public UnionFind(int size) {
this.size = size;
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
public int find(int element) {
while (element != parent[element]) {
element = parent[element];
}
return element;
}
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
if (firstRoot == secondRoot) {
return;
}
parent[firstRoot] = secondRoot;
}
/**
* 本并查集使用数组实现,为了更直观地看清内部数据,采用打印数组
*/
private void printArr() {
for (int parent : this.parent) {
System.out.print(parent + "\t");
}
System.out.println();
}
public static void main(String[] args) {
int n = 10;
UnionFind union = new UnionFind(n);
System.out.println("初始:");
union.printArr();
System.out.println("连接了5 6");
union.unionElements(5, 6);
union.printArr();
System.out.println("连接了1 2");
union.unionElements(1, 2);
union.printArr();
System.out.println("连接了2 3");
union.unionElements(2, 3);
union.printArr();
System.out.println("连接了1 4");
union.unionElements(1, 4);
union.printArr();
System.out.println("连接了1 5");
union.unionElements(1, 5);
union.printArr();
System.out.println("1 6 是否连接:" + union.isConnected(1, 6));
System.out.println("1 8 是否连接:" + union.isConnected(1, 8));
}
}
并查集:快速union,快速find,基于重量
思路和例子
其实上面讲的union函数,没有采取合理的手段去进行合并。每次都以secondElement为主,每次合并两个集合都让secondElement的根来继续充当合并之后的根。这样很可能达到线性的链表的状态。
那合并的时候怎么处理更好呢?
比如:有下面两个集合。其中 2 和 6 是两个集合的根。下面要让这两个集合合并,但是,合并之后只能有一个老大啊,到底谁来当呢?
在基于重量的union里,谁的人手多,就由谁来当合并之后的大哥。
2元素有4个手下,再算上自己,那就是5个人。
6元素有2个手下,再算上自己,那就是3个人。
很明显是2元素的人手多,所以2来充当合并之后的根节点。

代码
public class UnionFind {
private int[] parent;
private int[] weight;
private int size;
public UnionFind(int size) {
this.parent = new int[size];
this.weight = new int[size];
this.size = size;
for (int i = 0; i < size; i++) {
this.parent[i] = i;
this.weight[i] = 1;
}
}
public int find(int element) {
while (element != parent[element]) {
element = parent[element];
}
return element;
}
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
//如果已经属于同一个集合了,就不用再合并了。
if (firstRoot == secondRoot) {
return;
}
if (weight[firstRoot] > weight[secondRoot]) {
parent[secondRoot] = firstRoot;
weight[firstRoot] += weight[secondRoot];
} else {//weight[firstRoot] <= weight[secondRoot]
parent[firstRoot] = secondRoot;
weight[secondRoot] += weight[firstRoot];
}
}
private void printArr(int[] arr){
for(int p : arr){
System.out.print(p+"\t");
}
System.out.println();
}
public static void main(String[] args) {
int n = 10;
UnionFind union = new UnionFind(n);
System.out.println("初始parent:");
union.printArr(union.parent);
System.out.println("初始weight:");
union.printArr(union.weight);
System.out.println("连接了5 6 之后的parent:");
union.unionElements(5, 6);
union.printArr(union.parent);
System.out.println("连接了5 6 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 2 之后的parent:");
union.unionElements(1, 2);
union.printArr(union.parent);
System.out.println("连接了1 2 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了2 3 之后的parent:");
union.unionElements(2, 3);
union.printArr(union.parent);
System.out.println("连接了2 3 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 4 之后的parent:");
union.unionElements(1, 4);
union.printArr(union.parent);
System.out.println("连接了1 4 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 5 之后的parent:");
union.unionElements(1, 5);
union.printArr(union.parent);
System.out.println("连接了1 5 之后的weight:");
union.printArr(union.weight);
System.out.println("1 6 是否连接:" + union.isConnected(1, 6));
System.out.println("1 8 是否连接:" + union.isConnected(1, 8));
}
}
并查集:快速union,快速find,基于高度(基于秩)
思路
上面介绍的是,当两个集合合并时,谁的重量大,谁就来当合并之后的根。是比以前好多了。但还是有并查集深度太深的问题。并查集越深,就越接近线性,find函数就越接近O(n)
所以有了这种基于高度的union。合并时,谁的深度深,谁就是新的根。这样集合的深度最多是最大深度的集合的深度,而不会让深度增加。
比如上面的例子中,元素2的深度是2,元素6的深度是3,按基于重量的union合并后,新的集合深度是4。
但是如果不比重量,而是比高度呢?
那就是6的深度是3,2的深度是2。3大于2, 所以6是新集合的根。看下面图。 可以看到按高度合并后,新的结合的深度并没有加深,深度为3,而按基于重量的合并后的高度是4。

其他的地方与前面类似,只是大家可能对这段代码有疑惑。我来画个图讲解一下。
if (height[firstRoot] < height[secondRoot]) {
parent[firstRoot] = secondRoot;
} else if (height[firstRoot] > height[secondRoot]) {
parent[secondRoot] = firstRoot;
} else {
parent[firstRoot] = secondRoot;
height[secondRoot] += 1;
}
代码中的if 和 else if两种情况应该好理解。两个集合的高度不一样的时候,对它们进行合并,新集合高度肯定等于高度大的那个集合的高度。所以高度不用调整。
而两个集合高度相等时,哪个根来当新集合的根已经无所谓了,只需要让其中一个指向另一个就好了。然后会发现深度加了一层,所以新集合的根的高度就得+1,看下面图。

代码
public class UnionFind {
private int[] parent;
private int[] height;
int size;
public UnionFind(int size) {
this.size = size;
this.parent = new int[size];
this.height = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
height[i] = 1;
}
}
public int find(int element) {
while (element != parent[element]) {
element = parent[element];
}
return element;
}
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
if (height[firstRoot] < height[secondRoot]) {
parent[firstRoot] = secondRoot;
} else if (height[firstRoot] > height[secondRoot]) {
parent[secondRoot] = firstRoot;
} else {
parent[firstRoot] = secondRoot;
height[secondRoot] += 1;
}
}
/*
如果要合并的两个集合高度一样,那么随意选一个作为根
我这里选的是让secondRoot作为新集合的根。
然后secondRoot高度高了一层,所以+1
*/
private void printArr(int[] arr){
for(int p : arr){
System.out.print(p+"\t");
}
System.out.println();
}
public static void main(String[] args) {
int n = 10;
UnionFind union = new UnionFind(n);
System.out.println("初始parent:");
union.printArr(union.parent);
System.out.println("初始height:");
union.printArr(union.height);
System.out.println("连接了5 6 之后的parent:");
union.unionElements(5, 6);
union.printArr(union.parent);
System.out.println("连接了5 6 之后的height:");
union.printArr(union.height);
System.out.println("连接了1 2 之后的parent:");
union.unionElements(1, 2);
union.printArr(union.parent);
System.out.println("连接了1 2 之后的height:");
union.printArr(union.height);
System.out.println("连接了2 3 之后的parent:");
union.unionElements(2, 3);
union.printArr(union.parent);
System.out.println("连接了2 3 之后的height:");
union.printArr(union.height);
System.out.println("连接了1 4 之后的parent:");
union.unionElements(1, 4);
union.printArr(union.parent);
System.out.println("连接了1 4 之后的height:");
union.printArr(union.height);
System.out.println("连接了1 5 之后的parent:");
union.unionElements(1, 5);
union.printArr(union.parent);
System.out.println("连接了1 5 之后的height:");
union.printArr(union.height);
System.out.println("1 6 是否连接:" + union.isConnected(1, 6));
System.out.println("1 8 是否连接:" + union.isConnected(1, 8));
}
}
并查集优化:路径压缩
思路
路径压缩就是处理并查集中的深的结点。实现方法很简单,就是在find函数里加上一句 parent[element] = parent[parent[element]];就好了,就是让当前结点指向自己父亲的父亲,减少深度,同时还没有改变根结点的weight(非根节点的weight改变了无所谓)。
注:只能在基于重量的并查集上改find函数,而不能在基于高度的并查集上采用这种路径压缩。因为路径压缩后根的重量不变,但高度会变,然而高度改变后又不方便重新计算。
代码
public class UnionFind {
private int[] parent;
private int[] weight;
private int size;
public UnionFind(int size) {
this.parent = new int[size];
this.weight = new int[size];
this.size = size;
for (int i = 0; i < size; i++) {
this.parent[i] = i;
this.weight[i] = 1;
}
}
public int find(int element) {
while (element != parent[element]) {
parent[element] = parent[parent[element]];
element = parent[element];
}
return element;
}
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
//如果已经属于同一个集合了,就不用再合并了。
if (firstRoot == secondRoot) {
return;
}
if (weight[firstRoot] > weight[secondRoot]) {
parent[secondRoot] = firstRoot;
weight[firstRoot] += weight[secondRoot];
} else {//weight[firstRoot] <= weight[secondRoot]
parent[firstRoot] = secondRoot;
weight[secondRoot] += weight[firstRoot];
}
}
private void printArr(int[] arr){
for(int p : arr){
System.out.print(p+"\t");
}
System.out.println();
}
public static void main(String[] args) {
int n = 10;
UnionFind union = new UnionFind(n);
System.out.println("初始parent:");
union.printArr(union.parent);
System.out.println("初始weight:");
union.printArr(union.weight);
System.out.println("连接了5 6 之后的parent:");
union.unionElements(5, 6);
union.printArr(union.parent);
System.out.println("连接了5 6 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 2 之后的parent:");
union.unionElements(1, 2);
union.printArr(union.parent);
System.out.println("连接了1 2 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了2 3 之后的parent:");
union.unionElements(2, 3);
union.printArr(union.parent);
System.out.println("连接了2 3 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 4 之后的parent:");
union.unionElements(1, 4);
union.printArr(union.parent);
System.out.println("连接了1 4 之后的weight:");
union.printArr(union.weight);
System.out.println("连接了1 5 之后的parent:");
union.unionElements(1, 5);
union.printArr(union.parent);
System.out.println("连接了1 5 之后的weight:");
union.printArr(union.weight);
System.out.println("1 6 是否连接:" + union.isConnected(1, 6));
System.out.println("1 8 是否连接:" + union.isConnected(1, 8));
}
}
相关练习题
杭电ACM-1213-How Many Tables
链接:http://acm.hdu.edu.cn/showproblem.php?pid=1213
Today is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
翻译:N个人要坐在桌子上吃饭,但是人们拒绝和陌生人坐在一张桌子上。什么样的不算陌生人呢?主要是朋友的朋友的朋友的.....只要能扯上关系就不算陌生人。能扯上关系就可以坐在一张桌子上。所以至少要准备多少张桌子?
思路:其实就是对并查集进行合并操作,只要俩人认识,就组队。把队组好以后,看最后有多少个组(集合)就行了。最初每个人都自成一组,所以有多少人就有多少组。但是随着他们组队,每两个组合并成一个组,总的组数就会少1。如果组队的时候发现,他俩已经早就‘扯上关系了’,也就表名他俩早就是一组了,那就不用继续合并了,也就不用再 -1 了。
代码:
class UnionFind {
private int[] parent;
private int[] weight;
private int size;//代表并查集中元素个数
private int groups;//代表并查集中有多少个集合(小组)
public UnionFind(int size) {
this.parent = new int[size];
this.weight = new int[size];
this.size = size;
this.groups = size;//因为初始的时候每个人自成一组,所以有多少人就有多少组
for (int i = 0; i < size; i++) {
this.parent[i] = i;
this.weight[i] = 1;
}
}
public int find(int element) {
while (element != parent[element]) {
parent[element] = parent[parent[element]];
element = parent[element];
}
return element;
}
public boolean isConnected(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
//如果已经属于同一个集合了,就不用再合并了。
if (firstRoot == secondRoot) {
return;
}
if (weight[firstRoot] > weight[secondRoot]) {
parent[secondRoot] = firstRoot;
weight[firstRoot] += weight[secondRoot];
} else {//weight[firstRoot] <= weight[secondRoot]
parent[firstRoot] = secondRoot;
weight[secondRoot] += weight[firstRoot];
}
//合并 firstElement 和 secondElement 所在的两个组后,就少了一组。
this.groups--;
}
public int getGroups() {
return this.groups;
}
}
public class Main {
public static void main(String[] args) {
java.util.Scanner scanner = new java.util.Scanner(System.in);
int times = scanner.nextInt();
for (int i = 0; i < times; i++) {
int size = scanner.nextInt();
UnionFind union = new UnionFind(size);
int input = scanner.nextInt();
for (int j = 0; j < input; j++) {
//因为测试数据是从1开始,而我们的并查集是从数组的第0位开始
int first = scanner.nextInt() - 1;
int second = scanner.nextInt() - 1;
union.unionElements(first, second);
}
System.out.println(union.getGroups());
}
}
}
杭电ACM-1232-畅通工程
连接:http://acm.hdu.edu.cn/showproblem.php?pid=1232
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
思路:与上面题思路一样,在并查集中进行合并操作,求出最后剩下多少个组(集合)。这些组之间是互相不可达的。假如有M个组,那其实再需要M-1条连线就可以把他们连接起来了。所以组数 - 1 就是最后答案
代码:
class UnionFind {
/**
* 记录并查集对应位置的父亲结点位置
*/
private int[] parent;
/**
* 记录并查集对应结点的重量
*/
private int[] weight;
/**
* 表示并查集的元素个数
*/
private int size;
/**
* 表示并查集中集合的个数(组数)
*/
private int groups;
public UnionFind(int size) {
this.size = size;
this.groups = size;
this.parent = new int[size];
this.weight = new int[size];
for (int i = 0; i < size; i++) {
this.parent[i] = i;
this.weight[1] = 1;
}
}
public int find(int element) {
while (element != parent[element]) {
parent[element] = parent[parent[element]];
element = parent[element];
}
return element;
}
public boolean isConneted(int firstElement, int secondElement) {
return find(firstElement) == find(secondElement);
}
public void unionElements(int firstElement, int secondElement) {
int firstRoot = find(firstElement);
int secondRoot = find(secondElement);
if (firstRoot == secondRoot) {
return;
}
if (weight[firstRoot] < weight[secondRoot]) {
parent[firstRoot] = secondRoot;
weight[secondRoot] += weight[firstRoot];
} else {
parent[secondRoot] = firstRoot;
weight[firstRoot] += secondRoot;
}
this.groups--;
}
public int getGroups(){
return this.groups;
}
}
public class Main {
public static void main(String[] args) {
java.util.Scanner scanner = new java.util.Scanner(System.in);
int size = scanner.nextInt();
while(size!=0){
int input = scanner.nextInt();
UnionFind union = new UnionFind(size);
for(int i = 0;i<input;i++){
//因为测试数据中是从1开始技术。而我们的并查集是从0开始,所以每个输入都减1
int first = scanner.nextInt() - 1;
int second = scanner.nextInt() - 1;
union.unionElements(first,second);
}
//最后剩下的组数 - 1 就是最后的答案。因为连接M组的话,需要M-1条连线就可以了
System.out.println(union.getGroups() - 1);
size = scanner.nextInt();
}
}
}
学如不及,犹恐失之


 浙公网安备 33010602011771号
浙公网安备 33010602011771号