高精度加法

     高精度加法模拟常规的立竖式相加方法，各位对齐，诸位相加，如果相同位数上的数字大于10

则向前一位进一

高精度加法需要注意的问题：

1、运算法则     

同传统立竖式相加的方法，诸位对齐相加

2、进位   

  两种策略，一种是边计算边进位，第二种方式，加完以后进位

  边计算边进位，如下图所示：

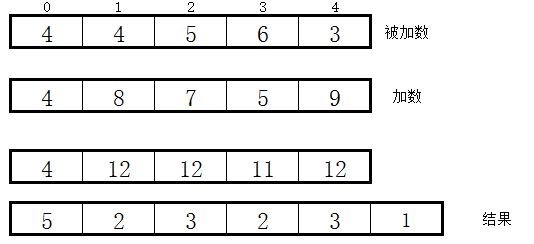
上图中，数组第一位存储数的长度

最后进位，如下图所示：

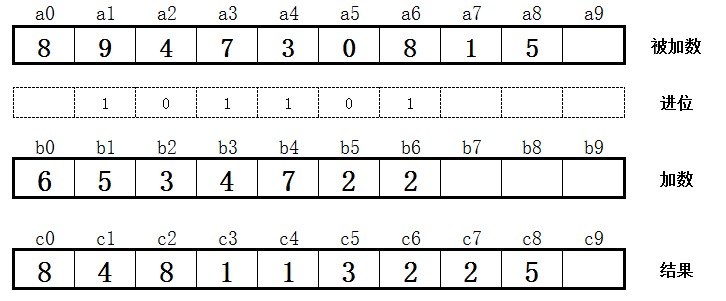
3、结果的位数确定

     被加数和加数中，取位数最大的数的长度，结果的位数，最大只可能是最长位数+1

高精度加法，代码实现如下：

#include <iostream>
#include <cstring>
using namespace std;
const int N =1001;
int aa[N],bb[N],cc[N]; //定义计算数和输出结果
 
void inputNum(string ss,int a[]); //输入需要计算的数保存到数组
void printArr(int a[]);  //输出数组的元素
void jisuan(int a[],int b[],int c[]);
 
int main()
{
    string s1 ="36895434535";
    string s2 ="46775492743";
    inputNum(s1,aa);
    printArr(aa);
    
    inputNum(s2,bb);
    printArr(bb);
    jisuan(bb,aa,cc);
    printArr(cc);
    return 0;
}
 
void jisuan(int a[],int b[],int c[])
{
    int x =0;  //临时保存的进位数
    int lenc =1;  //结果的开始位置
    while (lenc<=a[0] || lenc<=b[0])
    {
        c[lenc] =a[lenc]+b[lenc]+x;
        x = c[lenc]/10;
        c[lenc]%=10;
        lenc++;
    }
    c[lenc] =x;  //处理最后一个进位，结果是最大长度+1时，需要处理进位 
    
    while (c[lenc] ==0)  //求输出的结果有几位，赋值给结果数组的第0个元素
    {
        lenc--;
    }
    c[0]=lenc;
}
 
void inputNum(string ss,int a[])
{
    int len = ss.length();
    a[0] = len;
    for (int i=0;i<len;i++)
    {
        a[len-i] = ss[i] - 48;//字符变成数字，并且倒序存储
    }
}
void printArr(int a[])
{
    for (int i=a[0];i>0;i--)
    {
        cout<<a[i];
    }
    cout<<endl;
}

采用最后进位时，只需要改变上面代码中jisuan函数，代码如下

void jisuan(int a[],int b[],int c[])
{
    int i;
    if(a[0]>b[0])  
      c[0]=a[0];
    else
      c[0]=b[0];
    for(i=1;i<=C[0];i++)
    {
        c[i]+=a[i]+b[i];
        c[i+1]+=c[i]/10;
        c[i]%=10;
    }
    if(c[c[0]+1]>0) //求结果的位数 
      c[0]++;
    
}