二项树与二项堆

二项树与二项堆

一、概念

1. 二项树

二项树是一种递归定义的有序树，其递归定义如下：
$（1）二项树B_0只有一个节点；$
$（2）二项树B_k由两颗二项树B_{k-1}组成，其中一棵树是另一棵树的根的最左儿子。$
如下图所示：

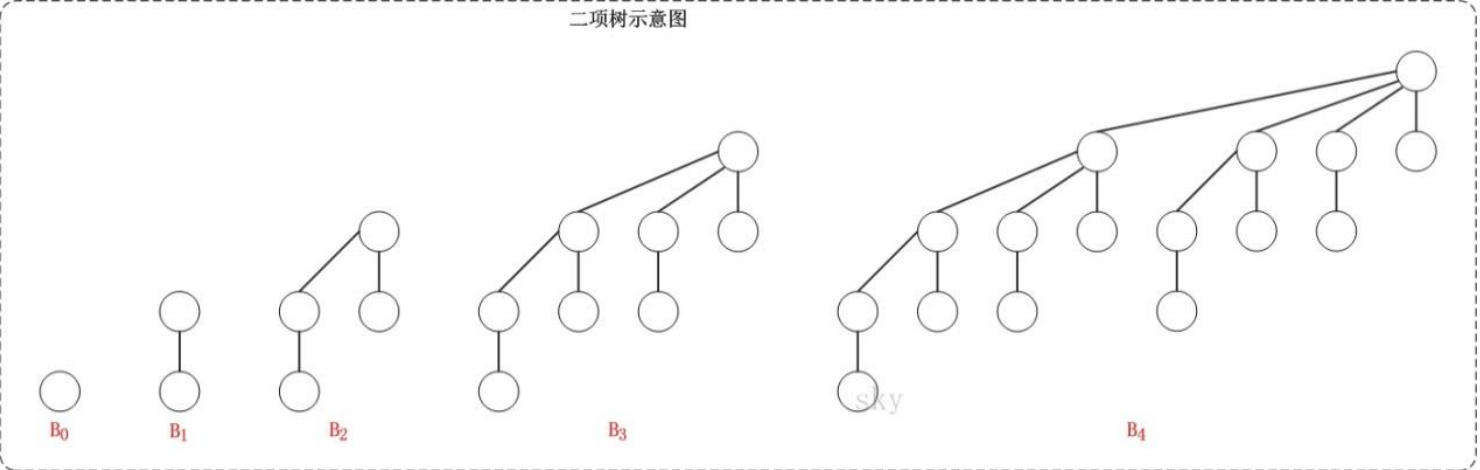
二项树具有如下性质：
$（1）B_k有2^k个节点；$
$（2）B_k的高度为k；$
$（3）B_k在深度i处恰好有C_k^i个节点，i\in [0,k]；$
$（4）根的度数为$k$，它大于任何其它节点的度数，并且如果根的儿子从左到右编号为k - 1,k - 2, ... , 0,儿 子i是子树B_i的根。$

2. 二项堆

二项堆是指满足以下性质的二项树的集合：
$（1）每颗二项树都满足最小（大）堆性质；$
$（2）不能有两棵或以上的二项树具有相同的度数(包括度数为0)。$
对于一个有$n$个节点的二项堆，它将有$[logn]+1$棵树，且树的类型与$n$的二进制位一一对应，如$n=13(1101)_2$，则该二项堆有$B_3,B_2,B_0$三棵树。如图所示：

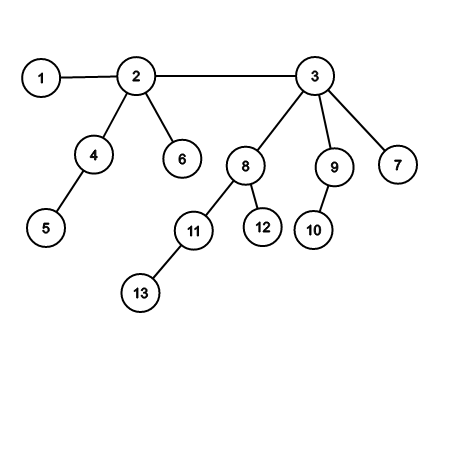
二项堆各操作：

建立	合并	查找最小值	查找节点	插入节点	删除节点
O(1)	O(logn)	O(logn)	O(logn)	O(logn)（均摊O(1)）	O(logn)

二、代码

合并：
现将两个二项堆中的二项树利用归并为度数单调不降的根链表，之后将其合并为新二项堆，过程类似模拟二进制加法。

点击查看代码

#ifndef BINOMIALHEAP_H
#define BINOMIALHEAP_H
template<class T>
class BinomialHeapNode
{
public:
    BinomialHeapNode<T> *parent, *child, *pre, *next;
    T value;
    int degree;
    BinomialHeapNode()
    {
        parent = child = pre = next = nullptr;
        value = T();
        degree = 0;
    }
    explicit BinomialHeapNode(T value)
    {
        parent = child = pre = next = nullptr;
        this->value = value;
        degree = 0;
    }
};

template<class T>
class BinomialHeap
{
private:
    BinomialHeapNode<T> *root;
    void release(BinomialHeapNode<T> *now)
    {
        if (now->child != nullptr)release(now->child);
        if (now->next != nullptr)release(now->next);
        delete now;
    }
    /*
     * 将两个二项堆的树的根表合并为度数单调递增的链表
     */
    static BinomialHeapNode<T> *mergeRoot(BinomialHeapNode<T> *root1, BinomialHeapNode<T> *root2)
    {
        BinomialHeapNode<T> *root = nullptr, *tail = nullptr;
        while (root1 != nullptr || root2 != nullptr)
        {
            BinomialHeapNode<T> *tmp = nullptr;
            if (root2 == nullptr || (root1 != nullptr && root1->degree <= root2->degree))
                tmp = root1, root1 = root1->next;
            else tmp = root2, root2 = root2->next;

            if (root == nullptr)root = tail = tmp;
            else tail->next = tmp, tmp->pre = tail, tail = tmp;
        }
        return root;
    }
    /*
     * 将两个度数相同的树合并
     */
    static void link(BinomialHeapNode<T> *child, BinomialHeapNode<T> *parent)
    {
        child->parent = parent;
        child->next = parent->child;
        if (parent->child != nullptr)parent->child->pre = child;
        parent->child = child;
        parent->degree++;
    }
    /*
     * 合并两个二项堆
    */
    static BinomialHeapNode<T> *combine(BinomialHeapNode<T> *root1, BinomialHeapNode<T> *root2)
    {
        BinomialHeapNode<T> *root = mergeRoot(root1, root2);
        //返回为空指针说明两个堆都是空的
        if (root == nullptr)
            return nullptr;
        BinomialHeapNode<T> *pre = nullptr, *now = root, *next = now->next;
        while (next != nullptr)
        {
            /*
             *根据当前相邻三棵树的种类，总共三种情况：
             *1.当前根与下一个根度数不同，说明树的类型不同，不做处理；
             *2.当前根、下一个根、再下一个根度数都相同，则跳过当前根，合并下两个；
             *3.当前根度数只与下一个根相等，根据两根值的大小进行合并。
            */
            if ((now->degree != next->degree) ||
                (next->next != nullptr && next->degree == next->next->degree))
            {
                pre = now;//pre 用来在之后连边
                now = next;
            }
            else if (now->value <= next->value)
            {
                now->next = next->next;
                next->pre = nullptr;//next在link中修改
                if (next->next != nullptr)next->next->pre = now;
                link(next, now);
            }
            else
            {
                if (pre == nullptr)root = next, next->pre = nullptr;
                else pre->next = next, now->pre = nullptr, next->pre = pre;
                link(now, next);
                now = next;
            }
            next = now->next;
        }
        return root;
    }
public:
    int size;
    BinomialHeap()
    {
        root = nullptr;
        size = 0;
    }
    ~BinomialHeap() { if (root != nullptr)release(root); }
    bool isEmpty() { return root == nullptr; }
    /*
     *  将heap合并到当前堆中
     */
    void merge(BinomialHeap<T> heap) { root = combine(root, heap.root); }
    void insert(T value)
    {
        auto *node = new BinomialHeapNode<T>(value);
        root = combine(root, node);
        size++;
    }
    /*
     * 获得最小值所在根节点
     */
    BinomialHeapNode<T> *getMinimumNode()
    {
        BinomialHeapNode<T> *now = root, *result = root;
        T minValue = result->value;
        while (now != nullptr)
        {
            if (now->value < minValue)result = now, minValue = now->value;
            now = now->next;
        }
        return result;
    }
    /*
     * 获得最小值
     */
    T getMinimum()
    {
        BinomialHeapNode<T> *node = getMinimumNode();
        return node->value;
    }
    /*
     * 删除最小值
     */
    void removeMinimum()
    {
        BinomialHeapNode<T> *node = getMinimumNode(), *heapNode = node->child;
        if (node == root)root = root->next;//如果是根节点需要换根
        if (node->pre != nullptr)node->pre->next = node->next, node->pre = nullptr;
        if (node->next != nullptr)node->next->pre = node->pre, node->next = nullptr;
        BinomialHeapNode<T> *now = heapNode;
        while (now != nullptr)now->parent = nullptr, now = now->next;
        delete node;
        size--;
        root = combine(root, heapNode);
    }
    /*
     * 没必要但姑且写一下删除某个特定值的方法：
     * 1.找到该点；
     * 2.将该点不断与父亲节点交换，直到其为根；
     * 3.断掉该点，将其子树合并回去即可。
     */
};

#endif //BINOMIALHEAP_H