P2510 [HAOI2008]下落的圆盘

题意

考虑算出每个圆能露出的部分，我们可以枚举它之后的圆，算出它被覆盖多少。

我们可以通过极角序将周长变为\([0,2\pi]\)的区间，这样问题就变为了给出一些区间，问\([0,2\pi]\)被这些去区间覆盖后还剩多少。

计算圆\(b\)覆盖圆\(a\)：
先判断是否存在包含和相离的情况。

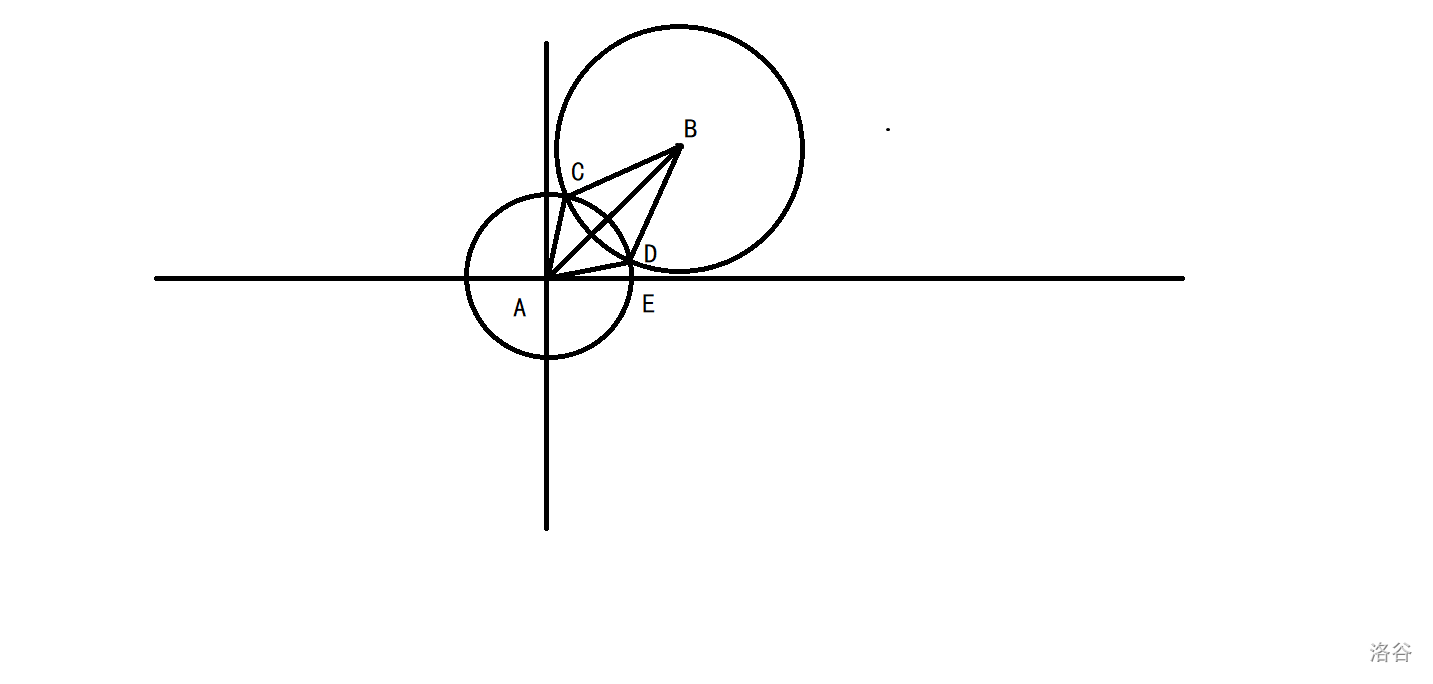
我们求出\(t1=\angle{EAB}\)和\(t2=\angle{DAB}\)，那么\(l=t1-t2,r=t1+t2\)。
如果\(l,r\)中有小于\(0\)的，就让它加上\(2\pi\)。
如果\(r<l\)那么覆盖的区间为\([l,2\pi],[0,r]\)。

code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
const double eps=1e-8;
const double Pi=acos(-1.0);
int n,m,tot;
double ans;
bool flag;
struct Point
{
    double x,y;
    inline double len(){return sqrt(x*x+y*y);}
    Point operator+(const Point a)const{return (Point){x+a.x,y+a.y};}
    Point operator-(const Point a)const{return (Point){x-a.x,y-a.y};}
    Point operator*(const double k){return (Point){x*k,y*k};}
    Point operator/(const double k){return (Point){x/k,y/k};}
    double operator*(const Point a)const{return x*a.y-y*a.x;}
    double operator&(const Point a)const{return x*a.x+y*a.y;}
};
inline int dcmp(double x)
{
	if(fabs(x)<=eps)return 0;
	return x<0?-1:1;
}
inline double dis(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Circle{Point p;double r;}cir[maxn];
struct Seq{double l,r;}seq[maxn<<1];
inline bool cmp(Seq a,Seq b){return !dcmp(a.l-b.l)?dcmp(a.r-b.r)<0:dcmp(a.l-b.l)<0;}
inline bool check1(Circle a,Circle b){return dcmp((b.r-(dis(a.p,b.p)+a.r)))>=0;}
inline bool check2(Circle a,Circle b){return dcmp(dis(a.p,b.p)-(a.r+b.r))>=0;}
inline double sqr(double x){return x*x;}
inline void work(Circle a,Circle b)
{
	double d,l,r,t1,t2;
	d=dis(a.p,b.p);
	t1=atan2(b.p.y-a.p.y,b.p.x-a.p.x);
	t2=acos((sqr(a.r)+sqr(d)-sqr(b.r))/(2.0*d*a.r));
	l=t1-t2,r=t1+t2;
	if(dcmp(l)<0)l+=2.0*Pi;
	if(dcmp(r)<0)r+=2.0*Pi;
	if(dcmp(l-r)<=0)seq[++tot]=(Seq){l,r};
	else seq[++tot]=(Seq){l,2.0*Pi},seq[++tot]=(Seq){0,r};
}
inline double solve(int x)
{
	for(int i=x+1;i<=n;i++)if(check1(cir[x],cir[i]))return 0;
	tot=0;
	for(int i=x+1;i<=n;i++)if(!check1(cir[i],cir[x])&&!check2(cir[i],cir[x]))work(cir[x],cir[i]);
	sort(seq+1,seq+tot+1,cmp);
	double res=0,now=0;
	for(int i=1;i<=tot;i++)
		if(seq[i].l>now)res+=seq[i].l-now,now=seq[i].r;
		else now=max(now,seq[i].r);
	res+=2*Pi-now;
	return res*cir[x].r;
}
int main()
{
	//freopen("test.in","r",stdin);
	//freopen("test.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%lf%lf%lf",&cir[i].r,&cir[i].p.x,&cir[i].p.y);
	for(int i=1;i<=n;i++)ans+=solve(i);
	printf("%.3lf",ans);
	return 0;	
}