FFT

一、 多项式的表示法：

1.系数表示法：

一个\(n-1\)的\(n\)项多项式\(f(x)\)可以表示为\(\sum\limits_{i=1}^{n-1}a_i*x^i\)。

于是可以用每一项的系数表示：\(f(x)=\{a_0,a_1,...a_{n-1}\}\)。

2.点值表示法：

将多项式看成一个函数，那么找\(n\)个不同的数\(x\)代入，可以得到\(n\)个不同的\(y\)。

显然这\(n\)对\((x,y)\)可以唯一确定一个多项式，因为这相当于\(n\)个方程的线性方程组。

写出来就是：\(f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),...,(x_{n-1},f(x_{n-1}))\}\)。

二、多项式乘法：

1.朴素算法：

我们现在要求\(h(x)=f(x)*g(x)\)。

我们分别考虑上两种表示法做乘法的复杂度：

<1>系数表示法：我们要枚举\(f(x)\)和\(g(x)\)的每一位系数相乘，复杂度显然为\(O(n^2)\)。
<2>点值表示法：两个点值表示法的多项式相乘是\(O(n)\)的！！！
举个例子：
\(f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),...,(x_{n-1},f(x_{n-1}))\}\)。
\(g(x)=\{(x_0,g(x_0)),(x_1,g(x_1)),...,(x_{n-1},g(x_{n-1}))\}\)。
那么我们只需要\(O(n)\)枚举每一位，便可得到：
\(h(x)=\{(x_0,f(x_0)*g(x_0)),(x_1,f(x_1)*g(x_1)),...,(x_{n-1},f(x_{n-1})*g(x_{n-1}))\}\)。

但是我们从系数表示转点值表示是\(O(n^2)\)的，从点值转系数还要\(O(n^3)\)消元。

系数表示法似乎无法优化，但是点值表示似乎有优化的空间。

2.复数

见OI-WIKI，讲的很详细。

3.单位复根

1.定义：

以下的\(n\)都是\(2\)的整次幂。

我们在系数表示转点值表示时会找\(n\)个不同的\(x_i\)代入，对于每个\(x_i\)，我们都要算出\(x_i^0,x_i^1,...,x_i^{n-1}\)，这显然是\(O(n^2)\)的。

我们考虑取一些特殊的\(x\)优化这个过程，比如我们可以找\(+1,-1,+i,-i\)，这些数的若干次方都是\(1\)，但是只找这\(4\)个显然是不够的。

现在我们在实轴和虚轴形成的坐标系中画一个单位圆，那么这个圆上的所有点都满足我们的要求，即若干次方后为\(1\)。

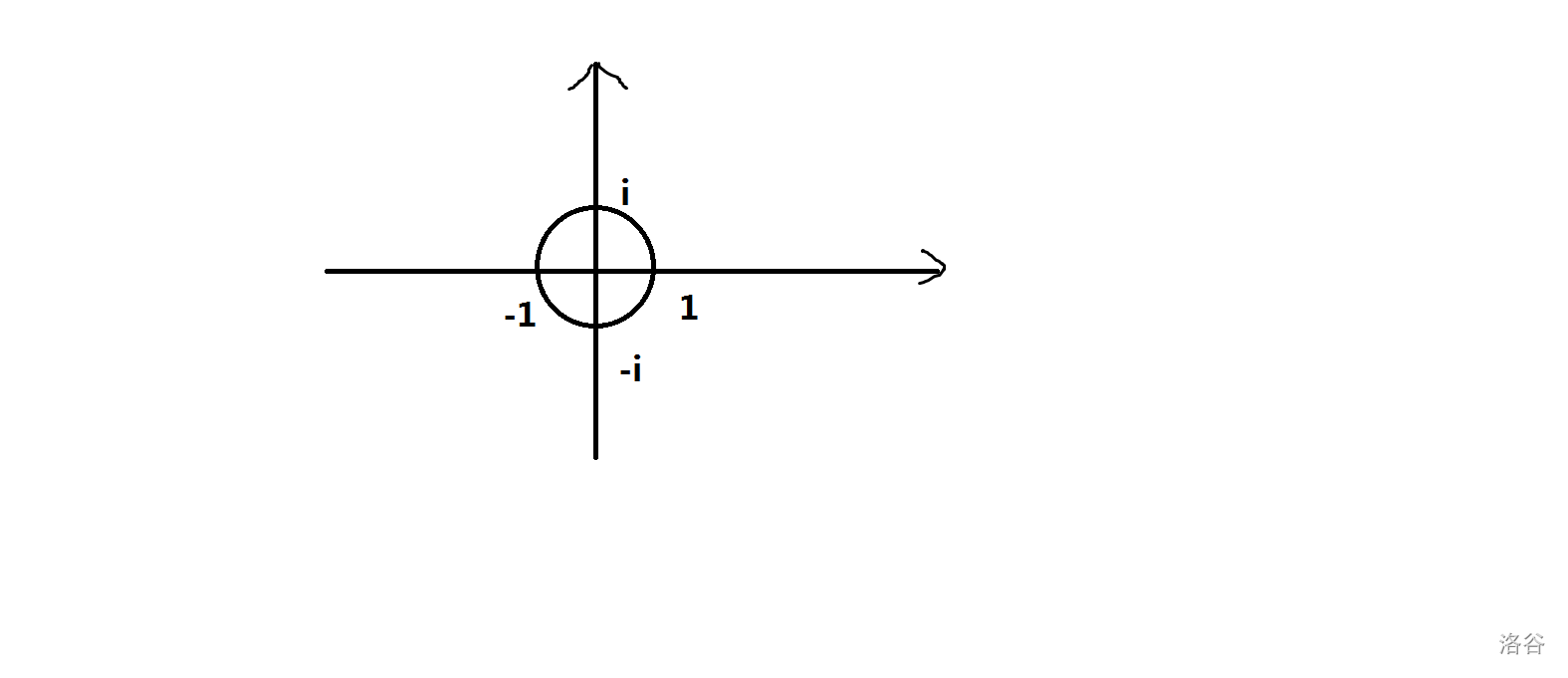
我们再将这个圆\(n\)等分，从\((1,0)\)开始标号，分别标为\(0,1,2,...,n-1\)。

比如\(n=8\)：

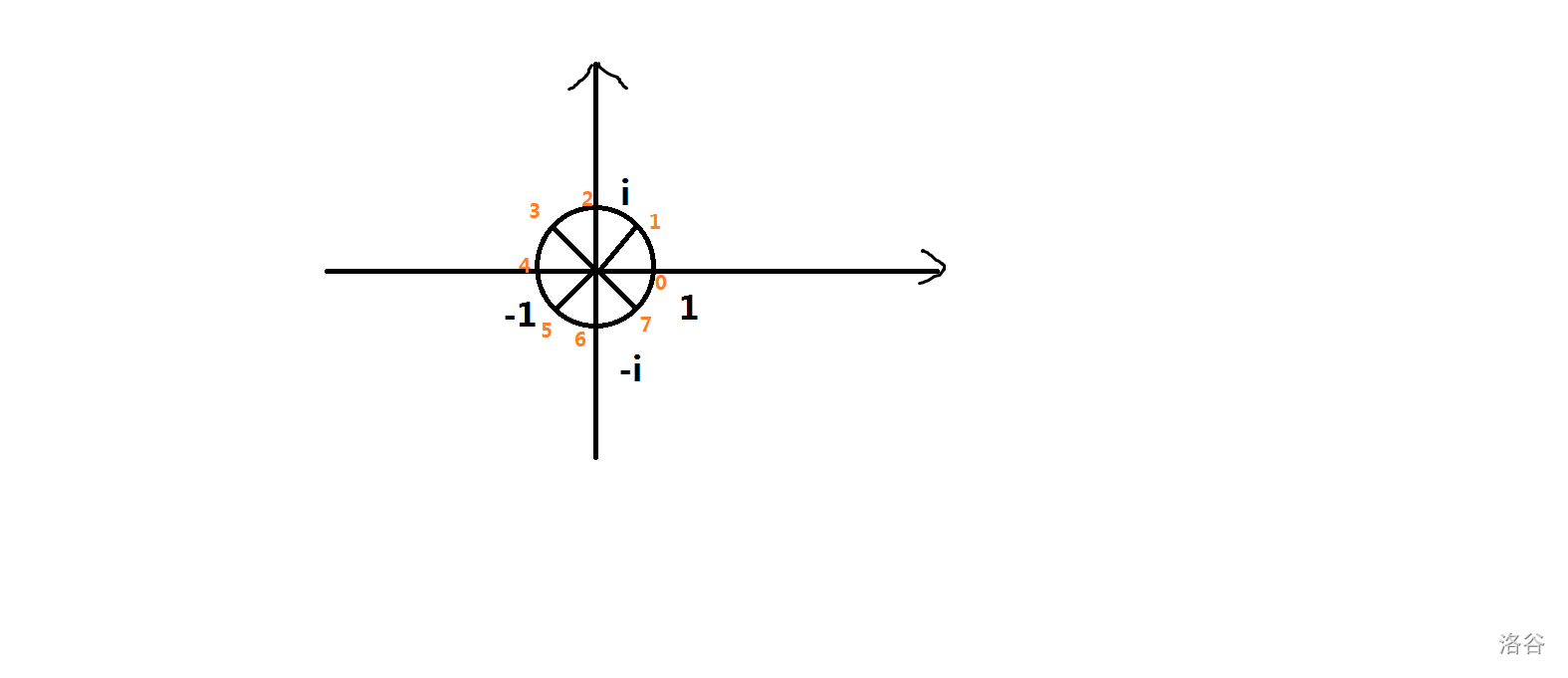
设\(\omega_n^k\)表示\(n\)等分时标号为\(k\)的点代表的值，根据复数的运算（模长相乘，角相加）可以得到：\(\omega_n^k=(\omega_n^1)^k\)。

我们将\(\omega_n^1\)称为\(n\)次单位根。

根据三角函数的公式可以推出\(\omega_n^k\)的公式：\(\omega_n^k=cos\frac{k}{n}2\pi+isin\frac{k}{n}2\pi\)。

于是\(\omega_n^0,\omega_n^1,..,\omega_n^{n-1}\)就是我们要代入的\(x_0,x_1,..,x_{n-1}\)。

2.性质：

<1>\(\omega_n^k=\omega_{2n}^{2k}\)

证明只需代入公式。

<2>\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)

证明：
\(w_n^{\frac{n}{2}}=cos\frac{n}{2}\frac{2\pi}{n}+isin\frac{n}{2}\frac{2\pi}{n}\)
\(=cos\pi+i*sin\pi\)
\(=-1\)
<3>\(\omega_n^n=\omega_n^0=1\)

现在我们找到了一组特殊的\(x\)，但是我们依旧要将每个\(x_i\)暴力代入算，所以复杂度仍然为\(O(n^2)\)。

三、FFT

上面那种方法叫做离散傅里叶变换（\(DFT\)），我们考虑分治。

假设我们有个多项式为\(f(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\)。

我们按照奇偶分类并将奇数类都提出一个\(x\)：
\(f(x)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3...+a_{n-1}x^{n-1})\)
\(=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+x(a_1+a_3x^2...+a_{n-1}x^{n-2})\)

此时我们定义另外两个多项式：
\(f1(x)=a_0+a_2x^1+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}\)
\(f2(x)=a_1+a_3x^1+...+a_{n-1}x^{\frac{n}{2}-1}\)

我们发现\(f(x)=f1(x^2)+xf2(x^2)\)！！！！

设\(k<\frac{n}{2}\)：

将\(\omega_n^k\)代入：

\(f(\omega_n^k)=f1((\omega_n^k)^2)+\omega_n^kf2((\omega_n^k)^2)\)
\(=f1(\omega_n^{2k})+\omega_n^kf2(\omega_n^{2k})\)
\(=f1(\omega_{\frac{n}{2}}^k)+\omega_n^kf2(\omega_{\frac{n}{2}}^{k})\)

将\(\omega_n^{k+\frac{n}{2}}\)代入：

\(f(\omega_n^{k+\frac{n}{2}})=f1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}f2(\omega_n^{2k+n})\)
\(=f1(\omega_n^{2k}\omega_n^n)-\omega_n^kf2(\omega_n^{2k}\omega_n^n)\)
\(=f1(\omega_n^{2k})+\omega_n^kf2(\omega_n^{2k})\)
\(=f1(\omega_{\frac{n}{2}}^k)-\omega_n^kf2(\omega_{\frac{n}{2}}^{k})\)

上面两个式子的结果除了符号不同以外完全相同，于是我们只要知道\(f1(\omega_{\frac{n}{2}}^k),f2(\omega_{\frac{n}{2}}^{k})\)，我们就能求出
\(f(\omega_n^k),f(\omega_n^{k+\frac{n}{2}})\)。

于是就可以递归分治了，复杂度显然是\(O(n\log_2n)\)的。

四、IFFT

我们用\(FFT\)求出了两个多项式乘积的点值表示\((x_i,y_i)\)，我们还要将其转为系数表示。

考虑怎么将点值表示快速转为系数表示：

这里有个结论：
一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数。

我们设\(c_k=\sum\limits_{i=0}^{n-1}y_i(\omega_n^{-k})^i\)。

那么\((c_i,w_n^{-i})\)就是多项式\(H(x)=y_0+y_1x+...+y_{n-1}x^{n-1}\)的点值表示。

先推一波式子：
\(c_k=\sum\limits_{i=0}^{n-1}y_i(\omega_n^{-k})^i\)
\(=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i\)
\(=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(\omega_n^j)^i)(\omega_n^{-k})^i\)
\(=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(\omega_n^j)^i(\omega_n^{-k})^i)\)
\(=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(\omega_n^{j-k})^i)\)

设\(S(x)=\sum\limits_{i=0}^{n-1}x^i\)。

当\(k!=0\)时：
代入\(\omega_n^k\)可得：
\(S(\omega_n^k)=1+\omega_n^k+(\omega_n^k)^2+...+(\omega_n^k)^{n-1}\)
两边同乘\(\omega_n^k\)得：
\(\omega_n^kS(\omega_n^k)=\omega_n^k+(\omega_n^k)^2+...+(\omega_n^k)^{n}\)
两式相减可得：
\((\omega_n^k-1)S(\omega_n^k)=(\omega_n^k)^n-1\)
于是可得：
\(S(\omega_n^k)=\frac{(\omega_n^k)^n-1}{\omega_n^k-1}\)
\(=\frac{(\omega_n^n)^k-1}{\omega_n^k-1}\)
\(=\frac{1-1}{\omega_n^k-1}\)
\(=0\)
当\(k=0\)时：
显然\(S(\omega_n^k)=n\)

回到之前的式子：
\(=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(\omega_n^{j-k})^i)\)

当\(j!=k\)时中间那个式子都是\(0\)
于是：
\(c_k=na_k\)
\(a_k=\frac{c_k}{n}\)
证完了。

五、迭代FFT

递归的常数太大，我们需要非递归的方法。

先放张经典图：

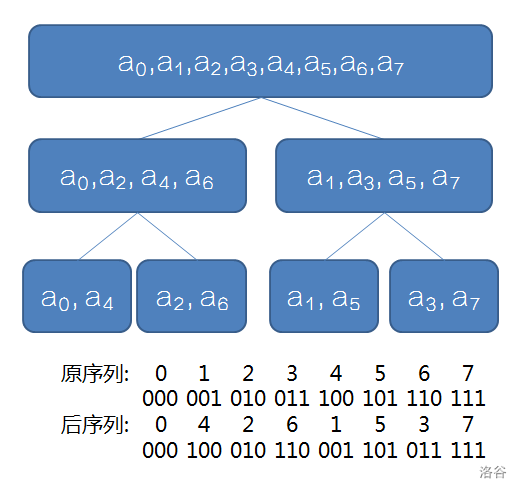
我们发现：
每个位置分治后的最终位置为其二进制翻转后得到的位置。

于是我们预先处理好每个数的最终位置，之后向上合并即可。

模板题

code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+10;
const double Pi=acos(-1.0);
int n,m,lim=1,len;
int pos[maxn];
struct cplx{double x,y;}a[maxn],b[maxn];
cplx operator+(cplx a,cplx b){return (cplx){a.x+b.x,a.y+b.y};}
cplx operator-(cplx a,cplx b){return (cplx){a.x-b.x,a.y-b.y};} 
cplx operator*(cplx a,cplx b){return (cplx){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
inline int read()
{
	char c=getchar();int res=0,f=1;
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')res=res*10+c-'0',c=getchar();
	return res*f;
}
void fft(cplx* a,int op)
{
	for(int i=0;i<lim;i++)if(i<pos[i])swap(a[i],a[pos[i]]);
	for(int mid=1;mid<lim;mid<<=1)
	{
		cplx wn=(cplx){cos(Pi/mid),op*sin(Pi/mid)};
		for(int i=0,r=mid<<1;i<lim;i+=r)
		{
			cplx w=(cplx){1,0};
			for(int j=0;j<mid;j++,w=w*wn)
			{
				cplx x=a[i+j],y=w*a[i+mid+j];
				a[i+j]=x+y;a[i+mid+j]=x-y;
			}
		}
	}
}
int main()
{
	n=read(),m=read();
	for(int i=0;i<=n;i++)a[i].x=read();
	for(int i=0;i<=m;i++)b[i].x=read();
	while(lim<=n+m)lim<<=1,len++;
	for(int i=0;i<lim;i++)pos[i]=(pos[i>>1]>>1)|((i&1)<<(len-1));
	fft(a,1);fft(b,1);
	for(int i=0;i<lim;i++)a[i]=a[i]*b[i];
	fft(a,-1);
	for(int i=0;i<=n+m;i++)printf("%d ",(int)(a[i].x/lim+0.5));
	return 0;
}