luoguP1646 [国家集训队]happiness
本篇篇幅过长,可能会出不少错,我已经查过一遍了,如果还有错恳请提出,我马上修改。
题意
这题有两种做法:
根据套路,先将所有愉悦值加上,之后减去最小代价。
1.
首先套路地,从源点\(s\)向每个点连选文科的价值,从每个点向汇点\(t\)连选理科的价值,割那条表示不选哪科,这样可以保证每个人不选文就选理。
接下来考虑如何处理这个限制:
只要点对\((i,j)\)中至少有一个不选文(理科同理),我们就要减去同选文的价值。
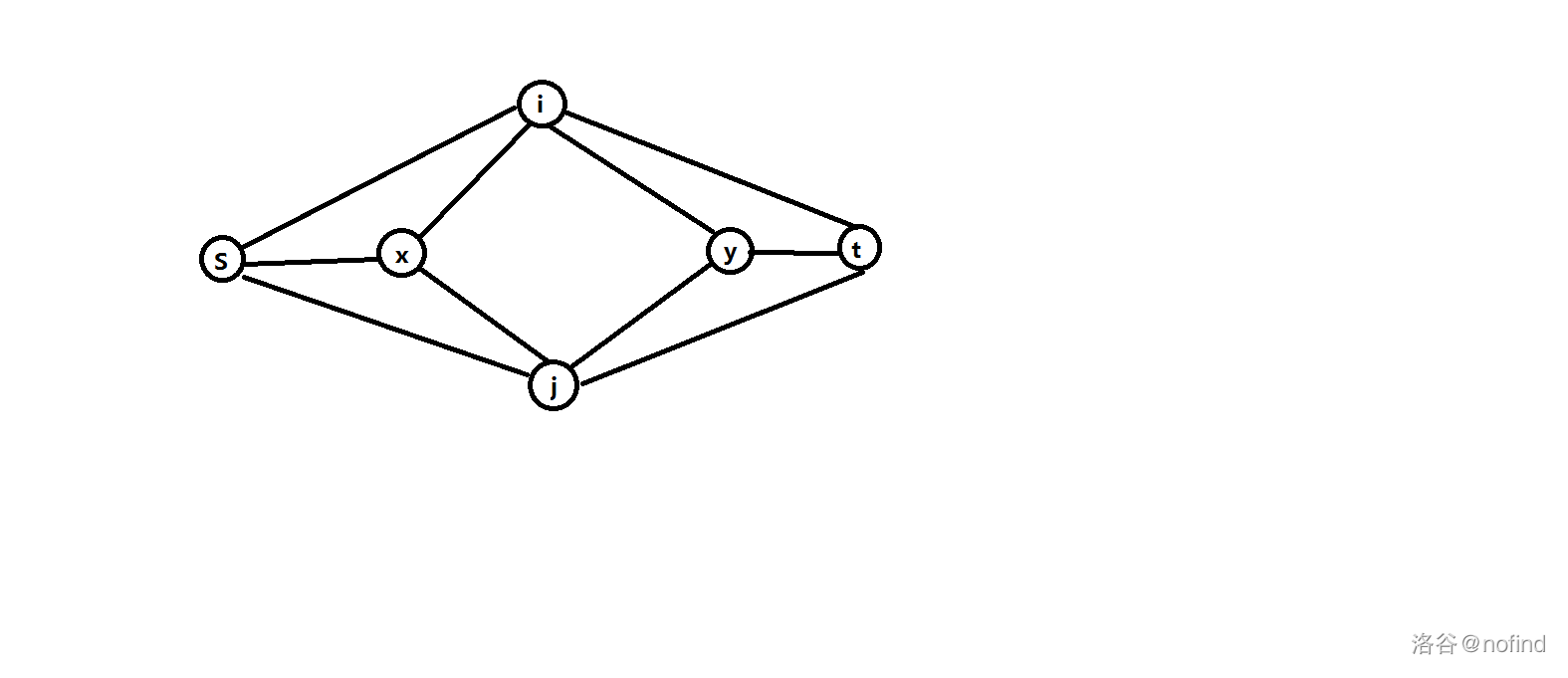
我们可以新建一个节点\(x\),从\(s\)向\(x\)连容量为\(i,j\)同选文的价值,之后从\(x\)向\(i,j\)连容量为\(inf\)的边。
我们发现这时如果\(i,j\)两点中有一个点理科边没有割(即不选文),那么此时就存在一条\(s-x-i/j-t\)这样一条路,我们只能割掉\(s-x\)这条边,因为如果割掉\(i/j-t\)这条边,那么我们可以不割\(s-i/j\)这条边,这与选文科不符,于是我们还是能保证每个人都选且只选了一科。
建出的图如下:
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=110;
const ll inf=1e18;
int n,m,cnt=1,tot=2,S,T;
int head[maxn*maxn*20],cur[maxn*maxn*20],dep[maxn*maxn*20];
ll ans;
struct edge{int to,nxt;ll flow;}e[maxn*maxn*40];
inline int id(int i,int j){return (i-1)*m+j;}
inline void add(int u,int v,ll w)
{
e[++cnt].nxt=head[u];
head[u]=cnt;
e[cnt].to=v;
e[cnt].flow=w;
}
inline void addflow(int u,int v,ll w){add(u,v,w);add(v,u,0);}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
for(int i=0;i<=tot;i++)cur[i]=head[i];
queue<int>q;
q.push(S);dep[S]=1;
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
if(dep[y]||e[i].flow<=0)continue;
dep[y]=dep[x]+1;q.push(y);
}
}
return dep[T]>0;
}
ll dfs(int x,int goal,ll lim)
{
if(x==goal||lim<=0)return lim;
ll res=lim;
for(int i=cur[x];i;i=e[i].nxt)
{
cur[x]=i;
int y=e[i].to;
if(e[i].flow<=0||dep[y]!=dep[x]+1)continue;
ll tmp=dfs(y,goal,min(res,e[i].flow));
if(tmp<=0)dep[y]=0;
res-=tmp;
e[i].flow-=tmp,e[i^1].flow+=tmp;
if(res<=0)break;
}
return lim-res;
}
inline ll Dinic()
{
ll res=0;
while(bfs())res+=dfs(S,T,inf);
return res;
}
int main()
{
scanf("%d%d",&n,&m);
S=0,T=n*m+1;
tot=n*m+1;
for(int i=1;i<=n;i++)
for(int j=1,x;j<=m;j++)
{
scanf("%d",&x);ans+=x;
addflow(S,id(i,j),x);
}
for(int i=1;i<=n;i++)
for(int j=1,x;j<=m;j++)
{
scanf("%d",&x);ans+=x;
addflow(id(i,j),T,x);
}
for(int i=1;i<n;i++)
for(int j=1,x;j<=m;j++)
{
scanf("%d",&x);ans+=x;
addflow(S,++tot,x);
addflow(tot,id(i+1,j),inf),addflow(tot,id(i,j),inf);
}
for(int i=1;i<n;i++)
for(int j=1,x;j<=m;j++)
{
scanf("%d",&x);ans+=x;
addflow(++tot,T,x);
addflow(id(i+1,j),tot,inf),addflow(id(i,j),tot,inf);
}
for(int i=1;i<=n;i++)
for(int j=1,x;j<m;j++)
{
scanf("%d",&x);ans+=x;
addflow(S,++tot,x);
addflow(tot,id(i,j+1),inf),addflow(tot,id(i,j),inf);
}
for(int i=1;i<=n;i++)
for(int j=1,x;j<m;j++)
{
scanf("%d",&x);ans+=x;
addflow(++tot,T,x);
addflow(id(i,j+1),tot,inf),addflow(id(i,j),tot,inf);
}
printf("%lld",ans-Dinic());
return 0;
}
2.
常规方法解方程。
还是经典老图:
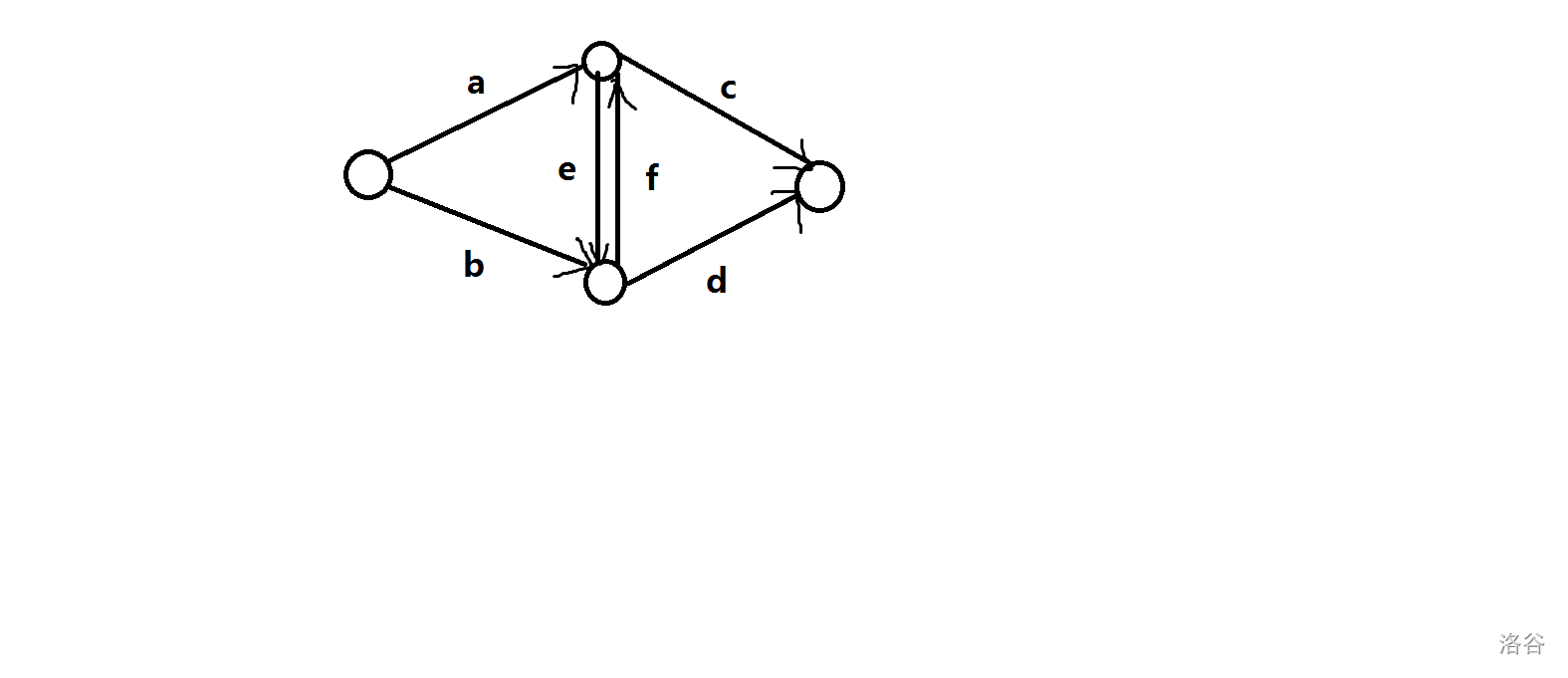
这里割哪条边表示不选哪科。
我们开始解方程:
先设\(a_i\)表示\(i\)选文科的价值,\(b_i\)表示\(i\)选理科的价值,\(c_{i,j}\)表示\(i,j\)同选文科的价值,\(d_{i,j}\)表示\(i,j\)同选理科的价值。
对于点对\((i,j)\)可以列出方程(以下方程按照“同文”,“同理”,“\(i\)文\(j\)理”,“\(i\)理\(j\)文”排序):
\(\begin{cases}c+d=b_i+b_j+d_{i,j}<1>\\ a+b=a_i+a_j+c_{i,j}<2>\\ a+d+f=b_i+a_j+c_{i,j}+d_{i,j}<3>\\b+c+e=a_i+b_j+c_{i,j}+d_{i,j}<4>\end{cases}\)
我们通过\(<3>+<4>-<1>-<2>\)可以得到:\(e+f=c_{i,j}+d_{i,j}\)
令\(e=f\),可得:\(e=f=\frac{c_{i,j}+d_{i,j}}{2}\)
我们令\(a=a_i+\frac{c_{i,j}}{2}\),即可解得其他变量的值:
\(b=a_j+\frac{c_{i,j}}{2}\)
\(c=b_i+\frac{d_{i,j}}{2}\)
\(d=b_j+\frac{d_{i,j}}{2}\)
于是我们就可以建图了,但是由于\(a,b,c,d,e,f\)不一定是整数,我们先整体乘2,最后除回去即可。
code:
#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
const int inf=1e9;
int n,m,cnt=1,S,T,ans;
int head[maxn*maxn*20],cur[maxn*maxn*20],dep[maxn*maxn*20];
struct edge{int to,nxt,flow;}e[maxn*maxn*40];
inline int read()
{
char c=getchar();int res=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9')res=res*10+c-'0',c=getchar();
return res*f;
}
inline int id(int i,int j){return (i-1)*m+j;}
inline void add(int u,int v,int w)
{
e[++cnt].nxt=head[u];
head[u]=cnt;
e[cnt].to=v;
e[cnt].flow=w;
}
inline void addflow(int u,int v,int w){add(u,v,w),add(v,u,0);}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
for(int i=S;i<=T;i++)cur[i]=head[i];
queue<int>q;
q.push(S);dep[S]=1;
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
if(dep[y]||e[i].flow<=0)continue;
dep[y]=dep[x]+1;q.push(y);
}
}
return dep[T]>0;
}
int dfs(int x,int goal,int lim)
{
if(x==goal||lim<=0)return lim;
int res=lim;
for(int i=cur[x];i;i=e[i].nxt)
{
cur[x]=i;
int y=e[i].to;
if(e[i].flow<=0||dep[y]!=dep[x]+1)continue;
int tmp=dfs(y,goal,min(res,e[i].flow));
if(tmp<=0)dep[y]=0;
res-=tmp;
e[i].flow-=tmp,e[i^1].flow+=tmp;
if(res<=0)break;
}
return lim-res;
}
inline int Dinic()
{
int res=0;
while(bfs())res+=dfs(S,T,inf);
return res;
}
int main()
{
n=read(),m=read();
S=0,T=n*m+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
int x=read();ans+=x;
addflow(S,id(i,j),x<<1);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
int x=read();ans+=x;
addflow(id(i,j),T,x<<1);
}
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
{
int x=read();ans+=x;
addflow(id(i,j),id(i+1,j),x);addflow(id(i+1,j),id(i,j),x);
addflow(S,id(i,j),x),addflow(S,id(i+1,j),x);//之前少加。
}
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
{
int x=read();ans+=x;
addflow(id(i,j),id(i+1,j),x);addflow(id(i+1,j),id(i,j),x);
addflow(id(i,j),T,x),addflow(id(i+1,j),T,x);
}
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
{
int x=read();ans+=x;
addflow(id(i,j),id(i,j+1),x);addflow(id(i,j+1),id(i,j),x);
addflow(S,id(i,j),x),addflow(S,id(i,j+1),x);
}
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
{
int x=read();ans+=x;
addflow(id(i,j),id(i,j+1),x);addflow(id(i,j+1),id(i,j),x);
addflow(id(i,j),T,x),addflow(id(i,j+1),T,x);
}
printf("%d",ans-(Dinic()>>1));
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号