基于DAT的中文分词方法的研究与实现
一、从Trie说起
DAT是Double Array Trie的缩写,说到DAT就必须先说一下trie是什么。Trie树是哈希树的一种,来自英文单词"Retrieval"的简写,可以建立有效的数据检索组织结构,trie中文叫做键树,也叫字典树,从名字就可以看出trie的实质是一个树。trie的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
基本性质:
1)根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2)从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3)每个节点的所有子节点包含的字符都不相同。
检索效率:
字典树trie 搜索关键码的时间和关键码自身及其长度有关,最快是0(1),即在第一层即可判断是否搜索到,最坏的情况是0(n), n为Trie树的层数。效率比哈希树高。
缺点:
占用空间较大。前面说了trie树本质上是哈希树的一种,所以在路由trie的时候,我们是通过一个哈希运算来查找当前节点的子节点的,假如我们的trie对包含1000个汉字的词汇表建树,那么为了每个节点均能通过完美哈希来找到子节点,那么每个节点中就必须预留一个1000大小的数组来保存子节点信息,但实际情况是,往往数据都是稀疏的,这导导致我们在追求效率的同时浪费了大量的空间。
二、Double array trie
双数组Trie (Double-Array Trie)结构由日本人JUN-ICHI AOE于1989年提出的,是Trie结构的压缩形式,仅用两个线性数组来表示Trie树,该结构有效结合了数字搜索树(Digital Search Tree)检索时间高效的特点和链式表示的Trie空间结构紧凑的特点。双数组Trie的本质是一个确定有限状态自动机(DFA),每个节点代表自动机的一个状态,根据变量不同,进行状态转移,当到达结束状态或无法转移时,完成一次查询操作。在双数组所有键中包含的字符之间的联系都是通过简单的数学加法运算表示,不仅提高了检索速度,而且省去了链式结构中使用的大量指针,节省了存储空间。
优点:
继承了Trie树的所有优点,同时又减少了空间开销。
缺点:
构造调整过程中,每个状态都依赖于其他状态,所以当在词典中插入或删除词语的时候,往往需要对双数组结构进行全局调整,灵活性能较差。 如果核心词典已经预先建立好并且有序的,并且不会添加或删除新词,那么这个缺点是可以忽略的。所以常用双数组Tire树都是载入整个预先建立好的核心分词词典。
三、举例说明
双数组Trie(Double-Array Trie)是trie树的一个简单而有效的实现,由两个整数数组构成,一个是base[],另一个是check[]。设数组下标为i ,如果base[i],check[i]均为0,表示该位置为空。如果base[i]为负值,表示该状态为一个词语的结束位置。Check[i]表示该状态的前一状态,用来检验跳转到此状态的前一状态是否为建立双数组时的前驱节点(t=base[i]+a, check[t]=i) 。
下面举例来说明用双数组Trie(Double-Array Trie)构造分词算法词典的过程。假定词表中只有“啊,阿根廷,阿胶,阿拉伯,阿拉伯人,埃及”这几个词,用Trie树可以表示。
首先对词表中所有出现的10个汉字进行编码:啊-1,阿-2,唉-3,根-4,胶-5,拉-6,及-7,廷-8,伯-9,人-10。。对于每一个汉字,需要确定一个base值,使得对于所有以该汉字开头的词,在双数组中都能放下。例如,现在要确定“阿”字的base值,假设以“阿”开头的词的第二个字序列码依次为a1,a2,a3……an,我们必须找到一个值i,使得base[i+a1],check[i+a1],base[i+a2],check[i+a2]……base[i+an],check[i+an]均为0。一旦找到了这个i,“阿”的base值就确定为i。用这种方法构建双数组Trie(Double-Array Trie),经过四次遍历,将所有的词语放入双数组中,然后还要遍历一遍词表,修改base值。因为我们用负的base值表示该位置为词语。如果状态i对应某一个词,而且Base[i]=0,那么令Base[i]=(-1)*i,如果Base[i]的值不是0,那么令Base[i]=(-1)*Base[i]。得到双数组Trie树如下图所示。
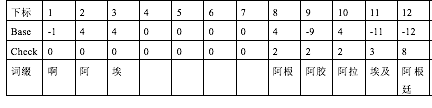
四、 DAT的实现
实现DAT的核心工作是找到每个字状态转移时的偏移量,即上图base数组中的值。由于在实际的计算中,我们要计算每个字(除词语结束位置)的后继结点在base和check数组中是否能找到空的位置,所以会有大量的查询当前字的兄弟节点和子节点的操作,因此我们可以预先建立一棵左儿子、右兄弟树来方便偏移量的计算。
a) 准备工作,生成左孩子、右兄弟树

1 const wchar * cnToks; 2 pCnTree CnTrie; 3 short tree_create_helper2(pCnNode root, wchar *word) 4 { 5 if(root == 0 && root->word != *word) return 1; 6 wchar *p = word; 7 pCnNode node = root; 8 while(*p) 9 { 10 if(*p == node->word){ 11 if(node->p_lefson == 0) 12 node->p_lefson = (pCnNode)calloc(1,sizeof(CnNode)); 13 node = node->p_lefson; 14 } 15 else if(node->word == 0){ 16 node->word = *p; 17 if(node->p_lefson == 0) node->p_lefson = (pCnNode)calloc(1,sizeof(CnNode)); 18 node = node->p_lefson; 19 } 20 else{ 21 pCnNode p_rightbrother; 22 if(node->p_rightbrother == 0) 23 node->p_rightbrother = (pCnNode)calloc(1,sizeof(CnNode)); 24 p_rightbrother = node->p_rightbrother; 25 26 while(p_rightbrother->word != 0 && p_rightbrother->p_rightbrother != 0 && p_rightbrother->word != *p) 27 p_rightbrother = p_rightbrother->p_rightbrother; 28 if(p_rightbrother->word == 0 ) p_rightbrother->word = *p; 29 else if(p_rightbrother->p_rightbrother == 0 && p_rightbrother->word != *p){ 30 p_rightbrother->p_rightbrother = (pCnNode)calloc(1,sizeof(CnNode)); 31 p_rightbrother = p_rightbrother->p_rightbrother; 32 p_rightbrother->word = *p; 33 } 34 35 if(p_rightbrother->p_lefson == 0) 36 p_rightbrother->p_lefson = (pCnNode)calloc(1,sizeof(CnNode)); 37 node = p_rightbrother->p_lefson; 38 } 39 40 p++; 41 42 } 43 44 if(node->word != 0 && node->word != WORDS_END_TAG){ 45 while(node->word != WORDS_END_TAG && node->p_rightbrother != 0) 46 node = node->p_rightbrother; 47 if(node->p_rightbrother == 0 && node->word != WORDS_END_TAG) 48 node->p_rightbrother = (pCnNode)calloc(1,sizeof(CnNode)); 49 node = node->p_rightbrother; 50 } 51 52 node->word = WORDS_END_TAG; 53 return 1; 54 } 55 static unsigned short tok_getIndex(wchar tok){ 56 int front, rear, half, res; 57 58 front = 0; rear = CnTrie->CnCuwCount - 1; res = 0xFFFF; // (-1) 59 while(rear - front > 1){ 60 half = (rear + front) / 2; 61 if(CnTrie->Cn_CUW[half] > tok){ 62 rear = half; 63 } 64 else { 65 front = half; 66 } 67 } 68 if(CnTrie->Cn_CUW[front] == tok) res = front; 69 if(CnTrie->Cn_CUW[rear] == tok) res = rear; 70 71 return res; 72 } 73 short tree_create_helper1(wchar *word) 74 { 75 wchar *p = word; 76 int index = tok_getIndex(*p); 77 if(index > 0 && index < 0xFFFF){ 78 if(CnTrie->CnNodeRoot[index] == 0){ 79 CnTrie->CnNodeRoot[index] = (CnNode *)calloc(1,sizeof(CnNode)); 80 CnTrie->CnNodeRoot[index]->word = *p; 81 } 82 pCnNode node = CnTrie->CnNodeRoot[index]; 83 84 tree_create_helper2(node,word); 85 } 86 return 1; 87 }
b) 计算状态跳转偏移量

1 buf[ndx] = 0; 2 int shift = toks_count; // 偏移量最小阀值 3 char conLoop = 1; ndx = 0; 4 for(;conLoop;shift++){ // 查找合适的偏移量,此处最耗时间, 5 conLoop = 0; 6 while(buf[ndx] != 0 && conLoop == 0){ 7 if(base[shift + buf[ndx]] != 0 || check[shift + buf[ndx]] != 0) 8 conLoop = 1; 9 ndx++; 10 } 11 ndx = 0; 12 } 13 shift--; // 注意:此处必须减1
c) 使用DAT做逆向最大分词匹配

1 while(*pwstr){ 2 shift = base[baseNdx]; tok = getIndex(*(++pwstr)); 3 if(check[shift+tok] == baseNdx){ 4 count++; 5 if(check[base[shift + tok] + 1] == shift + tok && base[base[shift+tok]+1] == -1){ 6 length = count; 7 ComWords_count++; 8 } 9 } 10 else{ 11 12 addWordToResult(length); 13 length = 0; 14 break; 15 } 16 baseNdx = shift+tok; 17 }
五、结束语
前面的内容主要讲了DAT的原理,及实现时的主要工作。由于原码篇幅比较长,所以第四部分的代码只粘了最主要的部分,看起来比较难董。在里我粘出项目的地址,有兴趣的可以自己看下源码。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号