平面点集的凸包计算
平面点集的凸包可理解为包含所有点的最小凸多边形(点可以在多边形边上或在其内)。这里给出一种求解方法。
一、基本思路
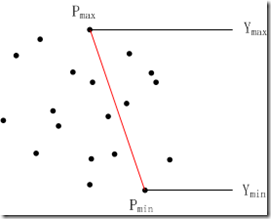
先找所有点中 y 坐标最大最小的点Pmax、Pmin,所找点必定是凸包上的点;
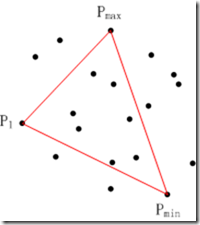
找距离直线PmaxPmin两侧最远的点P1,P0,构成初始三角形![]() ,
, ![]() ;
;
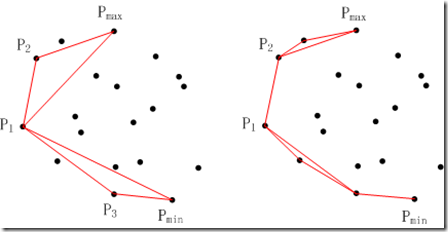
再对每个三角形新生成的边(![]() 、
、![]() 和
和![]() 、
、![]() )继续找与改变对应顶点(
)继续找与改变对应顶点(![]() )不在同一侧的最远点。
)不在同一侧的最远点。
二、算法流程
三、实现代码
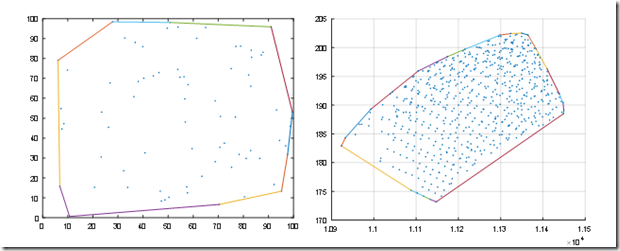
该算法由matlab实现:

1 clc; 2 clear; 3 N = 74; 4 DataPoints = [(1:N)', rand(N, 2).*100]; 5 plot(DataPoints(:, 2), DataPoints(:, 3), '.'); 6 % grid on; 7 X = DataPoints(:,2); 8 Y = DataPoints(:,3); 9 10 %% 11 % 根据 y 方向最值点确立初始三角形 12 % 找 y 最大和最小值的点 -------- 13 [Ymax, Ymax_i] = max(Y); 14 [Ymin, Ymin_i] = min(Y); 15 PymaxPymin = [X(Ymin_i) - X(Ymax_i), Y(Ymin_i) - Y(Ymax_i)]; 16 PtNum = N; 17 % 找距离直线 PymaxPymin 两侧最远点 -------- 18 PtNum_p = 1; PtNum_n = 1; 19 Dis_p = 0; Dis_n = 0; 20 for j = 1 : PtNum 21 PjPymax = [X(Ymax_i) - X(j), Y(Ymax_i) - Y(j)]; 22 PjPymin = [X(Ymin_i) - X(j), Y(Ymin_i) - Y(j)]; 23 Tri_erea = det([PjPymax; PjPymin]); 24 if Tri_erea < 0 25 if Dis_n < abs(Tri_erea) 26 Dis_n = abs(Tri_erea); 27 PtNum_n = j; 28 end 29 else 30 if Dis_p < Tri_erea 31 Dis_p = Tri_erea; 32 PtNum_p = j; 33 end 34 end 35 end 36 37 % 计算凸包边界 ---------- 38 TriStack = []; 39 TriStack(1, :) = [Ymax_i, Ymin_i, PtNum_p]; 40 TriStack(2, :) = [Ymax_i, Ymin_i, PtNum_n]; 41 Boundary = FindBoundary(TriStack, DataPoints); 42 hold on; 43 for i = 1 : size(Boundary, 1) 44 plot([X(Boundary(i,1)), X(Boundary(i,2))], ... 45 [Y(Boundary(i,1)), Y(Boundary(i,2))], '-'); 46 end

1 function TriPtNum_new = TriFindPt(TriPtNum, DataPoints) 2 % 扩展三角形的两边 3 % TriPtNum [i,j,k]是三角形 PiPjP 的顶点序号, 过顶点 P 的两边要扩展 4 % DataPoints 是所有点的坐标 5 % TriPtNum_new [i,j]是两条扩展边最外侧顶点序号, 若不存在取0 6 7 X = DataPoints(:,2); 8 Y = DataPoints(:,3); 9 % 点 Pi, Pj的对边, 扩展 ------------------- 10 PjP = [X(TriPtNum(3)) - X(TriPtNum(2)), Y(TriPtNum(3)) - Y(TriPtNum(2))]; 11 PiP = [X(TriPtNum(3)) - X(TriPtNum(1)), Y(TriPtNum(3)) - Y(TriPtNum(1))]; 12 PiPj = [X(TriPtNum(2)) - X(TriPtNum(1)), Y(TriPtNum(2)) - Y(TriPtNum(1))]; 13 % PiPj x PiP, PjPi x PjP, 向量叉积 14 PiPjxPiP = det([PiPj; PiP]); 15 PjPixPjP = det([-PiPj; PjP]); 16 17 % 找点 Pi, Pj 的对边距离最远点 ------------------ 18 PtNum = length(X); 19 PtNum_pi = 0; PtNum_pj = 0; 20 Dis_pi = 0; Dis_pj = 0; 21 for k = 1 : PtNum 22 % 点 Pi 的对边找最远点 23 PkPj = [X(TriPtNum(2)) - X(k), Y(TriPtNum(2)) - Y(k)]; 24 PkP = [X(TriPtNum(3)) - X(k), Y(TriPtNum(3)) - Y(k)]; 25 PkPjxPkP = det([PkPj; PkP]); 26 % 点 Pj 的对边找最远点 27 PkPi = [X(TriPtNum(1)) - X(k), Y(TriPtNum(1)) - Y(k)]; 28 PkPixPkP = det([PkPi; PkP]); 29 30 if(PiPjxPiP * PkPjxPkP < 0) 31 Tri_ereai = abs(PkPjxPkP); 32 if(Dis_pi < Tri_ereai) 33 Dis_pi = Tri_ereai; 34 PtNum_pi = k; 35 end 36 end 37 38 if(PjPixPjP * PkPixPkP < 0) 39 Tri_ereaj = abs(PkPixPkP); 40 if(Dis_pj < Tri_ereaj) 41 Dis_pj = Tri_ereaj; 42 PtNum_pj = k; 43 end 44 end 45 TriPtNum_new = [PtNum_pi, PtNum_pj]; 46 end

1 function Boundary = FindBoundary(TriStack, DataPoints) 2 % 从初始三角形开始查找边界 3 4 Boundary = []; 5 while size(TriStack, 1) 6 TriPtNum_new = TriFindPt(TriStack(end, :), DataPoints); 7 TriPt = TriStack(end, :); 8 TriStack(end, :) = []; 9 if TriPtNum_new(1) 10 TriStack(end+1, :) = [TriPt(:, 2:3), TriPtNum_new(1)]; 11 else 12 Boundary(end+1, :) = TriPt(:, 2:3); 13 end 14 if TriPtNum_new(2) 15 TriStack(end+1, :) = [TriPt(1, 1), TriPt(1, 3), TriPtNum_new(2)]; 16 else 17 Boundary(end+1, :) = [TriPt(1, 1), TriPt(1, 3)]; 18 end 19 end