python 有关于四舍五入，四舍六入的内容
一、简介
二、内容
三、问题
一、简介
最近看书看到了，有关python 内置的函数 round 取小数点的问题。书上描述的是四舍五入，然后又说，‘四舍五入’只是个约定的说法，并非所有的.5都会被进位。
然后我再上网查了下，才知道，之前使用的四舍五入后面，还有个四舍六入五成双
这时候我就产生了困惑，因为很多人都讲，四舍五入会导致数据增大，所以需要后面的方法，更加科学。
然后就有了下面的内容。
二、内容
1 两种方法的区别
1.1 四舍五入
在取小数近似数的时候，如果尾数的最高位数字是4或者比4小，就把尾数去掉。如果尾数的最高位数是5或者比5大，就把尾数舍去并且在它的前一位进"1",这种取近似数的方法叫做四舍五入法。
这个很简单，就是小学学过的。
1.35 ≈ 1.4 1.34 ≈ 1.3
1.3 ≈ 1 1.6 ≈ 2
0.56944 ≈ 0.6 不管尾巴有多长，看保留几位小数，就看小数位的后一位，大于等于5 进1， 小于5去掉。
1.2 四舍六入五成双
与上面的不同之处在于，多了些内容。就是在5的取舍上。
同样的保留3位小数，在后一位上面，大于5进1，小于5去掉。 并且， 如果等于5， 就看前一位数字，如果是奇数进1，偶数不变。
举例：统一保留三位小数
1.543500 ≈ 1.544 因为第四位小数是5，并且第三位小数是3 奇数，所以进1
1.544500 ≈ 1.544 因为第四位小数是5，并且第三位小数是4 偶数，所以不进1
1.544511 ≈ 1.545 因为第四位小数是5，但是5后面还有11，所以这个不用看奇偶，直接进1
1.3 python 中的round
在书上，好像描述的小数点的保留是按照 四舍六入五成双 执行的。但是我实际操作了下，并不是：
根据这些个测试，如果是四舍五入法，那么第三个就错了，而 四舍六入五成双 那就跟价不符合，第一个应该舍去。
通过查询后得知，这是由于计算机存储浮点数时转换成二进制导致的，虽然在图形上显示是两位小数，可是实际上未必如此。
这也是，我在运算中，尽量将小数点计算，换成整数运算，会降低误差。
有关round 浮点详细可以参照这篇博客：去看看
还有这篇关于不要看垃圾博客的内容并且详细讲了round和四舍五入的内容：去看看
因为我也要开始说一些人瞎说了。
2. 疑问
为什么四舍五入会导致数据偏大，就像这种解释，
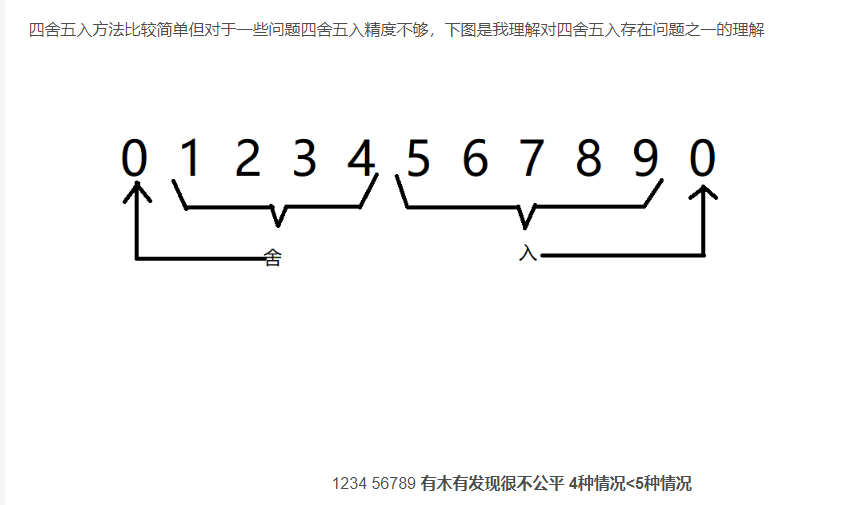
说实话，找了很多，都感觉说不通。
第一张图， 很明显，他自己都画出来了， 按道理应该是 0 1 2 3 4 和5 6 7 8 9 ，都是同样的数字，都是同样的长度，怎么就被他们说成了是 四个点跟五个点。
最后面的那个零，明显是取不到的
那么，四舍五入法，明显就是5 5 开，怎么都不可能就说哪边少了。
那可是为什么说，四舍六入五成双 要比 四舍五入法 高级呢？？？
2.1 浮点数运算失准问题
这里必须插一条，因为接下来需要涉及浮点运算问题，就必须说到浮点运算会丢失精度。比如下面的例子
# 验证浮点数在运算过程种出现的运算损失实验 import random # 验证加法失真 def check_add(): # 整数运算是不会失真的，这个值作为参考值 sum_real = 0 # 这个是浮点求和的参数 sum_float = 0.0 # 实验次数 10000次 for i in range(1, 10**4): # 生成0-100的随机数a a = random.randint(0, 100) # 生成浮点数 creat_float creat_float = a / 100 # 记录加a之前的值，后面好查看值 record_sum_real = sum_real record_sum_float = sum_float # 整数相加a sum_real += a # 浮点数加creat_float，这个作为累加器，直到浮点运算出错 sum_float += creat_float # 真实值的和值除以100， 然后转化为字符串 使其方便判断 sum_real_str = str(sum_real/100) sum_float_str = str(sum_float) # 判断值的计算是不是出现了偏差 if sum_real_str != sum_float_str: # 出现偏差，展示下面内容 dui_qi('这是第{}次循环'.format(i), ' ', '') print('值不相同') dui_qi('真实和字符串', 'sum_real_str', sum_real_str) dui_qi('浮点和字符串', 'sum_float_str', sum_float_str) print() dui_qi('本次随机数', 'a', a) dui_qi('本次随机数变成浮点数的值', 'creat_float', creat_float) dui_qi('上一次循环的真实和值', 'record_sum_real', record_sum_real) dui_qi('本次加完随机数的真实和值', 'sum_real', sum_real) dui_qi('上一次循环的浮点和值', 'record_sum_float', record_sum_float) dui_qi('本次加完随机数的浮点和值', 'sum_float', sum_float) break # 打印对齐的方法 def dui_qi(title, value_name, value): print("{0:{1}<20}{2:<20}:".format(title, chr(12288), value_name), value) if __name__ == '__main__': check_add()
运行结果
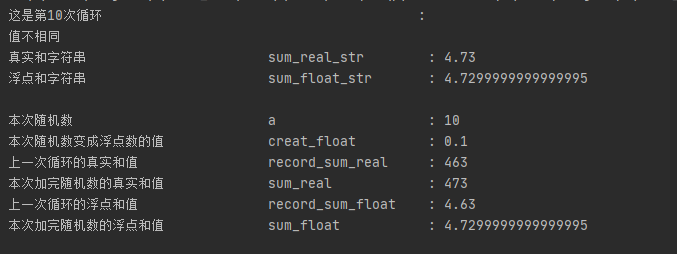
这个实验的核心，sum_real是对照组， sum_float是实验组，sum_real进行整数累加，sum_float进行浮点数累加
因为计算机整数相加不会丢失精度，而浮点会丢失，详细可以参考：去看看
而正常来讲，sum_real / 100 应该是等于 sum_float
但是实际上， 在上面的例子里，就出现了错误，
在第十次循环的时候，本来 sum_float + creat_float = 4.63 + 0.1 = 4.73
但是实际结果却是 4.7299999999999995。
这种失准会在小数点位数越多的过程种会逐渐放大。
同理，乘法，除法，减法，都会出现同样的问题。
2.2 怎么让浮点运算误差降低到最小
2.2.1 python的 decimal 模块
Decimal可用来保存具有小数点而且数值确定的数值，它不像float和real是用来保存近似值。
他几乎就是python用来处理浮点运算丢失精度的存在。
使用方法很简单， 将字符串小数 或者整数转入，就可以生成Decimal 对象。
注意：要传入字符串的小数点，直接传入小数，可能会导致传入值，直接偏差。
比如，
2.2.2 将浮点数先提升到整数，再进行运算。
例如： 在上面的方法进行略微修改
# 验证正常浮点数运算与decimal运算对比 # 使用decimal就可以避免精度损失 import random import decimal def check_(): # 整数运算是不会失真的，这个值作为参考值 sum_real = 0 # 这个是浮点求和的参数 变成Decimal对象 sum_float = 0 # 这个是decimal求和的参数 变成Decimal对象 sum_decimal = decimal.Decimal(0) # 这个是decimal求和的参数 变成Decimal对象 sum_upper = 0 max_a = 10 ** 7 # 实验次数 1000000次 for i in range(1, 10**6): # 生成0-100的随机数a a = random.randint(0, 10) # 生成浮点数 creat_float creat_float = a / max_a # 生成成Decimal对象 decimal_float decimal_float = decimal.Decimal(a) decimal_float /= max_a # 整数相加a sum_real += a # 浮点数加creat_float sum_float += creat_float # decimal求和加decimal_float sum_decimal += decimal_float # 先转换加decimal_float sum_upper += creat_float * max_a # 缩放对照值，方便对比 sum_real /= max_a sum_upper /= max_a dui_qi('整数运算和值', 'sum_real', sum_real) dui_qi('浮点运算和值', 'sum_float', sum_float) dui_qi('decimal运算和值', 'sum_decimal', sum_decimal) dui_qi('放大小数点运算和值', 'sum_upper', sum_upper) # 打印对齐的方法 def dui_qi(title, value_name, value): print("{0:{1}<20}{2:<20}:".format(title, chr(12288), value_name), value) if __name__ == '__main__': check_()
运行结果
从结果我们可以看出，当使用 decimal 和 将小数点先放大到整数运算都是可以避免精度损失的。
也就是说，放大到小数位越少，精度会越高。
但是归根究底，最好使用整数运算。
唉，感觉除法是计算机的天敌。
结论： decimal 和 放大浮点数到整数，可以有效避免浮点丢失精度的问题。
3. 实验
3.1 实验一 验证round 的最佳方式
由于上面说了，计算机存储浮点数，是使用的靠近方式，所以浮点运算会导致误差，所以round的保留小数点的方式并不完全与四舍五入和四舍六入的结果相同。可参考： 去看看
那么，我们要验证，如何能让round的结果更准确。
import random def work(liu_n, wei_n): """ 本次实验，只要是验证，round, 哪种情况下，与真实结果最接近 实验思路： 随机生成数字， 然后进行四舍五入， 获得三个值， 然后进行多次实验， 将三个数值分别求和， 看最终结果的偏差 :param liu_n: 保留小数位 :param wei_n: 保留小数位后面留几个数字 :return: None """ # 初始所有统计值 real_sum = round_sum_nothing = round_sum_upper = round_sum_upper_f = round_sum_upper_int = 0 # 将a缩小的倍数 low_b = pow(10, liu_n + wei_n) # 实验次数100万次 for i in range(10**6): # 生成随机数a，必须保正后面生成的小数为保留位的前一位 a = random.randint(0, pow(10, wei_n + 1)) # 合成标准数值，这是后面的方法四的对照组，用来参照用 # check_real_sum = real_sum # 合成对照组和值 real_sum += a # 将数值修改成保留位的小数 比如保留3位小数 末尾留2个数字，生成的a等于254， a就修改成 0.00254 a /= low_b # 方式一 不处理，直接进行四舍五入处理 nothing_val = round(a, liu_n) round_sum_nothing += nothing_val # 方式二 先放大后再缩小 然后浮点运算 upper_val = round(a * pow(10, liu_n))/pow(10, liu_n) round_sum_upper += upper_val # 方式三 先放大后再缩小，再放大，进行浮点运算 upper_f_val = upper_val * pow(10, liu_n) round_sum_upper_f += upper_f_val # 方式四 先放大后再缩小，再放大，转换成整数再运算 """ 此方式验证不通过，下面的代码是验证为什么不行的过程 当方式三 upper_val * max_n 放大的过程会导致浮点数出现丢失精度 然后 int的过程中，会直接去掉小数点后面的内容，而不是四舍五入，结果就会导致与真实结果偏差很大 """ # upper_int_val = int(upper_f_val) # round_sum_upper_int += upper_int_val # # f_3_str = str(round_sum_upper_f).split('.')[0] # f_4_str = str(round_sum_upper_int) # if f_3_str != f_4_str: # print('第{}次出现差异'.format(i)) # print('check_real_sum', check_real_sum) # print('a:', a) # print('real_sum', real_sum) # print('方式三的总和字符串', f_3_str) # print('方式4的总和字符串', f_4_str) # print('nothing_val：', nothing_val) # print('upper_val： ', upper_val) # print('upper_f_val：', upper_f_val) # print('upper_int_val：', upper_int_val) # print() # break print('真实和值：', real_sum) round_sum_nothing *= low_b round_sum_upper *= low_b round_sum_upper_f *= pow(10, wei_n) print('方式一：', round_sum_nothing, '绝对差值:', real_sum - round_sum_nothing) print('方式二：', round_sum_upper, '绝对差值:', real_sum - round_sum_upper) print('方式三：', round_sum_upper_f, '绝对差值:', real_sum - round_sum_upper_f) # print('方式四：', round_sum_upper_int, '绝对差值:', real_sum - round_sum_upper_int) # 固定保留小数位数，保留尾部长度变化 def test_wei(): for i in range(1, 10): print('测试保留{}位尾巴：'.format(i)) work(1, i) print() # 固定末尾数值，保留小数点的变化 def test_de(): for i in range(1, 10): print('测试保留{}位小数：'.format(i)) work(i, 1) print() if __name__ == '__main__': # work(3, 5) # test_wei() test_de()
实验结果，我这只放出部分图，大家有兴趣可以自己试试
从以上结果，我们可以发现，
1. 方式一，由于直接进行保留四舍五入的过程本来就由于浮点精度问题导致不准确，加上又是浮点相加，导致数据的跳动相当大，明显是不可取。
2. 方式二，从网上看的攻略，说是round 在一位小数取整的时候比较准确，所以我放大了a,
比如：让本来是 0.0325 保留2位小数，那么我让它先乘以100变成了3.25, 然后进行四舍五入取整， 变成3，然后再除100变成0.03.
通过这种方式，确实让round的结果提高了不少。
3. 方式三，其实这个是跟round无关，因为这是涉及浮点数丢失精度的问题，就是再方式二的基础上，也就是不除100， 让总值先进行整数运算。
结果就是，没有了那些个尾巴，结果更加准确。
结论一： 使用round保留小数位时，最好先放大再缩小，可以降低误差。
结论二： 浮点运算时，尽量放大到整数值，可以提高精度。
3.2 round, 四舍五入，四舍六入五成双 三个方法的对比。
import random from decimal import Decimal, ROUND_HALF_UP, ROUND_HALF_EVEN # 使用 decimal 模块进行 四舍五入法 def si_wu_decimal(de, n, up=True): # 制作format format_str = '{:.nf}'.replace('n', str(n)) # 制作保留小数位的目标格式 比如 0.00 decimal_format_str = format_str.format(0) # 将小数点转换成字符串，这样可以提高精确度 de = str(de) # 选用rounding # ROUND_HALF_UP 是 四舍五入法 # ROUND_HALF_EVEN 是 四舍六入五成双 rounding = ROUND_HALF_UP if not up: rounding = ROUND_HALF_EVEN # 使用 decimal 模块进行 四舍五入法 back = Decimal(de).quantize(Decimal(decimal_format_str), rounding=rounding) return back def work(liu_n, wei_n): """ 实验思路： 随机生成数字， 然后进行四舍五入，四舍六入五成双， 获得三个值， 然后进行多次实验， 将三个数值分别求和， 看最终结果的偏差 :param liu_n: 保留小数位 :param wei_n: 保留小数位后面留几个数字 :return: None """ # 初始所有统计值 real_sum = si_wu_sum = si_liu_sum = round_sum = 0 round_sum_sum_f = si_liu_sum_int = 0 # 将a缩小的倍数 low_b = pow(10, liu_n + wei_n) # 实验次数100万次 for i in range(10**6): # 生成随机数a，必须保正后面生成的小数为保留位的前一位 a = random.randint(0, pow(10, wei_n + 1)) # 合成对照组和值 real_sum += a # 将数值修改成保留位的小数 比如保留3位小数 末尾留2个数字，生成的a等于254， a就修改成 0.00254 a /= low_b # 由于 si_wu_decimal 会返回decimal对象，与decimal对象运算会自动将结果类型转换成decimal对象，所以不用处理浮点误差 si_wu_sum += si_wu_decimal(a, liu_n) si_liu_sum += si_wu_decimal(a, liu_n, False) # 根据实验一的结论 先放大后缩小 进行保留小数位后 然后放大浮点数，进行整数相加避免浮点误差 round_sum += round(a * pow(10, liu_n))/pow(10, liu_n) * low_b print('真实和值：', real_sum) si_wu_sum *= low_b si_liu_sum *= low_b print('四舍五入和值：', si_wu_sum, '绝对差值:', abs(real_sum - si_wu_sum)) print('四舍六入和值：', si_liu_sum, '绝对差值:', abs(real_sum - si_liu_sum)) print('python round和值：', round_sum, '绝对差值:', abs(real_sum - round_sum)) # 固定保留小数位数，保留尾部长度变化 def test_wei(): for i in range(1, 10): print('测试保留{}位尾巴：'.format(i)) work(1, i) print() # 固定末尾数值，保留小数点的变化 def test_de(): for i in range(1, 10): print('测试保留{}位小数：'.format(i)) work(i, 1) print() if __name__ == '__main__': test_wei() test_de() # work(3, 1)
实验结果
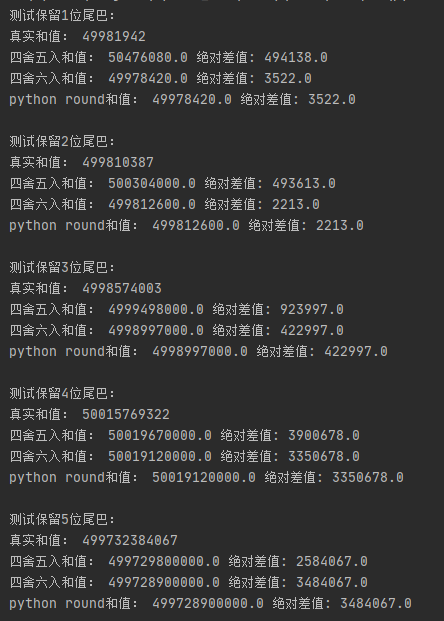
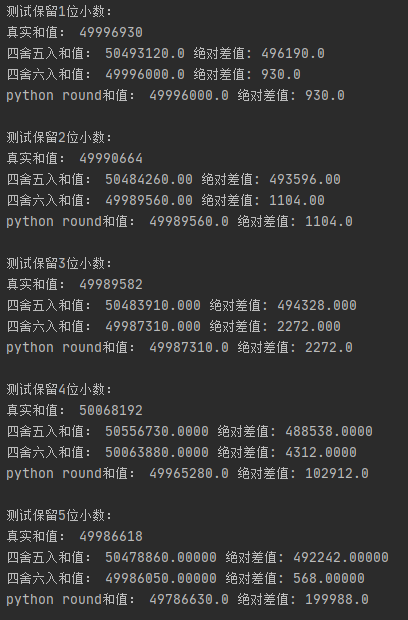
以上我们可以发现：
1.随着保留小数点位数的后面的尾巴越来长，三个方法的取向值是越来越接近的。
2.四舍六入 与 round的值基本一致，说明round的保留小数点的方式，确实是四舍六入五成双的方式相同，但是由于浮点运算导致的精度丢失，导致了结果出现了偏差。
这一点在变动保留位数，尾巴为1的实验中很明显，四舍六入 与 round的值基本一致，但是偶尔round的值就是突然差得很大。
3.也是非常重要的一点。 四舍五入确实误差要远远大于四舍六入，特别在保留小数点后面的尾巴越短的时候。
这就出现我们很大疑惑的地方，为什么？？
3.3 为什么四舍五入确实误差要远远大于四舍六入
要搞清楚这个，我们就得先知道，这种保留小数点位的方法是怎么偏移导致数据的偏差的。
我们选一个简单的小数。保留一位小数，小数尾巴为1位
比如 0.53 0.56
当保留小数时，我们看的就是 第二位小数 3和 6
那按照处理方法，
保留结果就是 0.5 0.6
那么偏差值就是 第一丢了0.03 ,第二个就多了0.04
如图
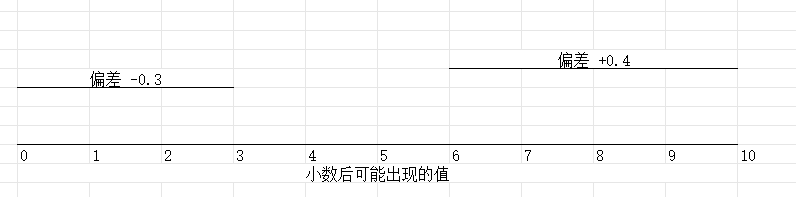
按照逻辑上来讲，0 1 2 3 4， 5 6 7 8 9 （10取不到）两边都是5个数， 两边取到的概率是相同的吧
但是，看上图就会知道，当我们保留小数位时，一定是要取值公平
当左边偏差是 - 0.3时， 右边也一定要有 + 0.3
这样才可以在多次实验的时候， 可以抵消误差，以达到最终值是接近标准值。
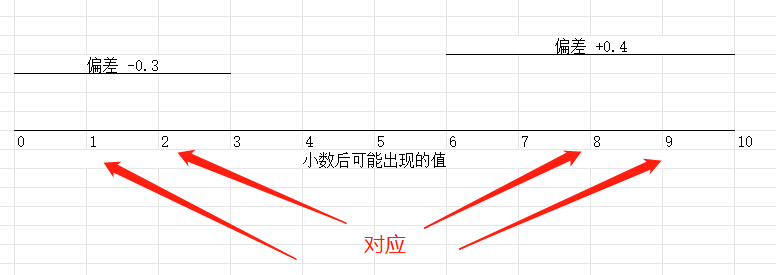
比如，当尾巴为 1时， 偏差为-0.4 ，但是又尾巴为9时对应， 偏差为+0.4
同理，2 跟8 3跟7
只唯独 0 跟 5 没有对应的。
0 本来是对应10 ，可是10取不到的点。
不过0 有一点好，虽然它没有对应点，但是经过保留小数点后，它会被去掉，偏差值为0， 所以它不会影响结果
而5 是个中心点，所以当我们在数据取到尾巴为 5 时，按照四舍五入就算是进一位了， 这样就会导致差值+0.5，这样就会导致随着实验次数增加，结果会偏得越大。
那么如何解决这个问题呢。
因为5，没有平衡，那我们就随机 二分之一 取就好了， 有时候遇到5 -0.5， 有时候遇到5就+0.5。
有没有感到熟悉感， 就是四舍六入五成双里面的， 当前一位为基数，就进1 ，当前一位为偶数就不进舍去，刚好是二分之一。
结论：1. 四舍五入确实误差要远远大于四舍六入。
2.使用四舍六入五成双时，前一位的取值必须是随机平均的，0 1 2 3 4 5 6 7 8 9 ，如果前一位值有明显特殊性，就不适用于四舍六入五成双。
3.当小数保留位后面的尾巴越长时，四舍五入与四舍六入五成双的结果是越接近的。
三、问题
1. 随着保留小数点位数的后面的尾巴越来长，两个方法的取向值为什么是越来越接近的？
两个方法导致偏差的是在取到 5 的时候，+0.5的偏差， 当随着尾巴越来越长时，取到 0.50 0.500 0.5000 0.50000的值概率是会越来越小的，也就导致了偏差值的减小。
