Codeforces1470B-Strange Definition

题目大意：定义若x与y的lcm除以gcd是一个数的平方，那么x与y是相邻的。给定n个数字，对这些数字进行变化，每次变化ai变为所有与其相邻的数字的乘积，q个询问，问变化w次，相邻数量的最大值。

题目链接

 

解题思路：首先对公式进行一个简单的变化

 

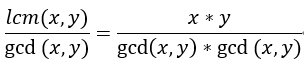
 想让x与y相邻，那么x*y需要是一个数的平方

将其进行质数分解，偶数次幂的质数对其没有贡献，我们将其删除，留下奇数次幂的质数

这么做的好处是，若x与y相邻，那么x==y

下面做一个简单的证明

若x与y相邻，那么x*y是一个数的平方，对这个结果进行质数分解一定是所有质数的幂为偶数，否则存在奇数次幂，该数不是一个数的平方。

若x==y，x与y所有幂次均相等，得x与y相邻。

证毕。

所以问题变成了n个数中出现最多的次数

考虑进行变化，若该数出现次数为偶数次，那么变化后该数变为1；若该数出现次数为奇数次，变化后该数仍为原数，所以答案仅有两种，当w为0时，答案为分解后出现次数最多的次数；当w不为0时，答案为max(ans(w==0),ans(num==1)+even)，就是数字为1和出现次数为偶数次的和与w==0时的答案取大值。

 

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<string.h>
 4 #include<math.h>
 5 #include<vector>
 6 using namespace std;
 7  
 8 const int maxn=1e6+5;
 9 typedef long long ll;
10 int n,m,t;
11 int a[maxn];
12 int pri[maxn],vis[maxn],sign[maxn],tot=0;
13 
14 void init(int n)
15 {
16     for(int i=2;i<=n;i++){
17         if(!vis[i]){
18             sign[i]=1;
19             pri[++tot]=i;
20         }
21         for(int j=1;j<=tot;j++){
22             if(i*pri[j]>n)
23                 break;
24             vis[i*pri[j]]=pri[j];
25             if(i%pri[j]==0)
26                 break;
27         }
28     }
29 }
30 vector<int> vec;
31 int sum[maxn];
32 int main()
33 {
34     init(1000000);
35     scanf("%d",&t);
36     while(t--)
37     {
38         int ans0=0,ans1=0,even=0;
39         vec.clear();
40         scanf("%d",&n);
41         for(int i=1;i<=n;i++)
42         {
43             scanf("%d",&a[i]);
44             int tmp=1,j=1;
45             while(a[i]>=pri[j]){
46                 int num=0;
47                 while(a[i]%pri[j]==0){
48                     num++;
49                     a[i]/=pri[j];
50                 }
51                 if(num%2)
52                     tmp*=pri[j];
53                 j++;
54                 if(sign[a[i]]){
55                     tmp*=a[i];
56                     break;
57                 }
58             }
59             vec.push_back(tmp);
60             ans0=max(ans0,++sum[tmp]);
61         }
62         for(int v : vec){
63             if(v!=1){
64                 if(sum[v]%2==0)
65                     even++;
66             }else {
67                 ans1++;
68             }
69         }
70         for(int v : vec){
71             sum[v]=0;
72         }
73         int q;
74         scanf("%d",&q);
75         while(q--){
76             ll w;
77             scanf("%lld",&w);
78             if(w==0){
79                 printf("%d\n",ans0);
80             } else{
81                 printf("%d\n",max(ans0,ans1+even));
82             }
83         }
84     }
85     return 0;
86 }
View Code

 

 posted on 2021-01-27 11:02  haianx  阅读(106)  评论(0)  编辑  收藏  举报