量化投资_金融市场分析之相位分析法(实现)
第一章:简介
我们如果把金融市场的价格走势进行归类的话,那么它是一种非线性的时间序列,第一:属于时间序列,因此可以用信号处理及计量经济学的一些模型来进行分析;第二:又是一种非线性的,所谓可以直观的理解为并不是具有一眼可以看得出的一种规律走势。
图1-1是一段K线图的价格走势,一般需要把复杂的问题简单化一些方便我们分析。因此只取他们的close价格并且把他们进行连线,像图1-2这样,close价格在进行量化投资分析时是具有比较重要的意义,close价格可以表示一段时刻具有重要参考意义的一种价格;顺便说一下。当天的结算价也是具有重要参考意义的。
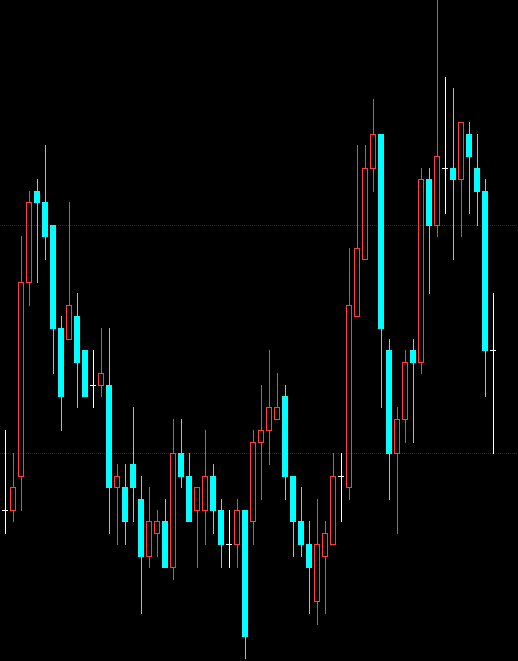
(图1-1)
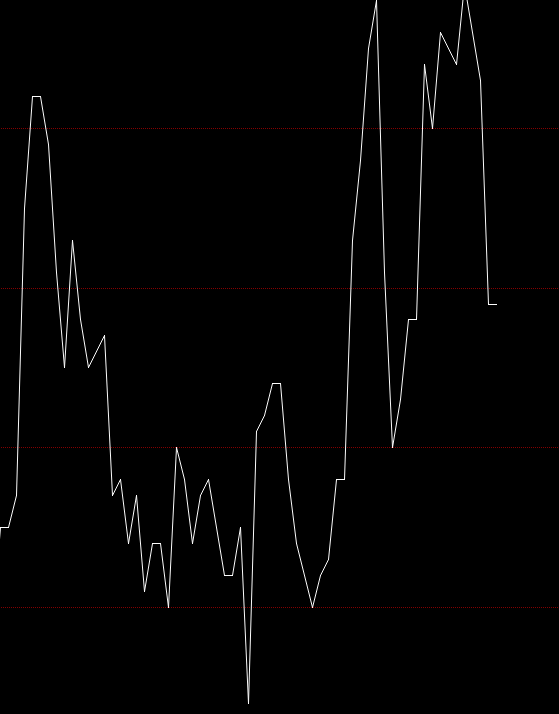
(图1-2)
那么问题就来了,分析这种非线性的时间序列有各种各样的方式,这里试图用信号处理中的相位分析方式来做一下研究,也给大家带来一种新的思路。在这里也借用广发金工的研究报告为蓝本进行分析(广发证券_金融工程年度论坛系列报告之十:相位指标在短线择时中的应用)
第二章:相位是什么?
百度百科的解释如下:
“所谓相位(phase)是对于一个波,特定时刻在它循环中的位置;一种它是否在波峰、波谷或者他们之间某点的标度。相位描述信号波形变化的度量,通常以度(角度)做为单位,也称作相角。当信号波形以周期的方式变化,波形循环一周记为360°。”。这种解释有点儿太抽象了。在知乎中也有相关的解释,解释的是比较直观的。具体可以参考链接:https://www.zhihu.com/question/31104681。形象的,如果现在一段波的走势是一个正弦波如图2-1。
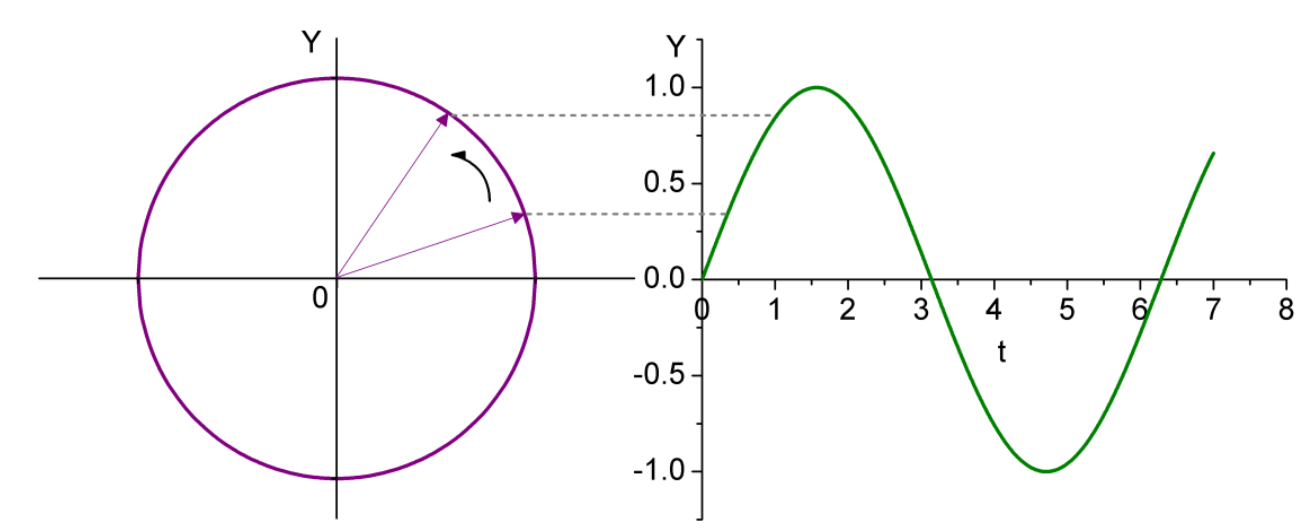
(图2-1)
因此任何一种波,我们都可以把它看做在一个圆中进行逆时针旋转的而形成的一个圆(波是正向走势,而通过相位变换形成一种圆的逆时针形成相位图),更加形象点儿的表示就是想水井打水一样,辘轳转轮控制着水桶的走势(图2-2)

(图2-2)
当然在后面我们需要把这个正弦波进行推广到非线性的时间序列,实际的时间序列并不是走的这么规整。
在形象的理解了相位之后,这里要问为什么要用相位。当然答案就是为了更好的分析嘛,我们在(图2-1)中可以看到在进行相位角旋转的时候,它会处于四个象限中;比如:
起涨时:处于第一象限
由涨起跌时:处于第二象限
处于完全跌势时:处于第三象限
由跌转涨时:处于第四象限
这样通过相位角的变化,我们可以看出,处于不同的象限内的数据点,非常直观的被投射到相位图中表示现在的走势处于那种状态中。
第三章:相位有关的几个术语和知识点
分别通过两张图来表示:
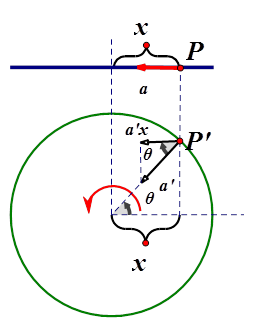
(图3-1)
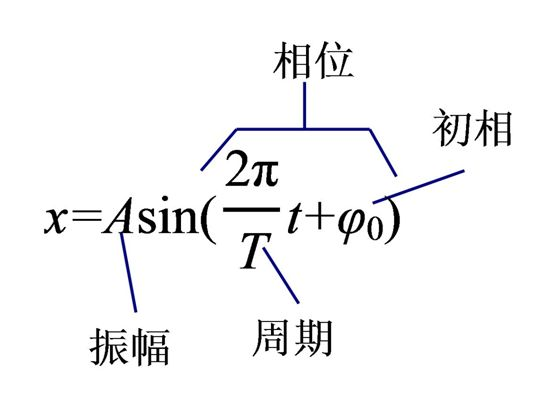
(图3-2)
第一章图反映某一时刻的相位变化,第二章图是对应的相关计算公式。其实公式也不难我们试着解释一下。
假设某一个时刻:现在数据(物体)处于P点,对应转轴运动上的小球位与图中的P',它与圆心的连线表示为OP',与水平向右方向的家教为θ,那么这个θ就成为相位角或者相位。
相位角会随着时间而发生变化。如果最初的t=0时θ=φ,那么φ成为初相位。随着P'点以角速度ω旋转,相位角会变为θ=ωt+φ。
这样,物体P'的水平坐标就可以求出来, x=Acos(ωt+φ),这就是运动质点P点的位移随时间的变化规律。
这里看起来是有一点儿让人懵逼了。我们在下面进行试着建模看一下是否能够解决上面的问题。
第四章:建模(根据:广发证券_金融工程年度论坛系列报告之十:相位指标在短线择时中的应用)
第一步:初始数据消噪
时间序列A = 长期趋势 + 短期波动 + 噪声;这一步是去除噪声的工作。
时间序列是由长期趋势、短期波动和噪声三者叠加。拿到初始数据后,首先要把噪声处理掉。原文用的MA进行消除噪声,这里采用DMA,系数暂定位0.25。
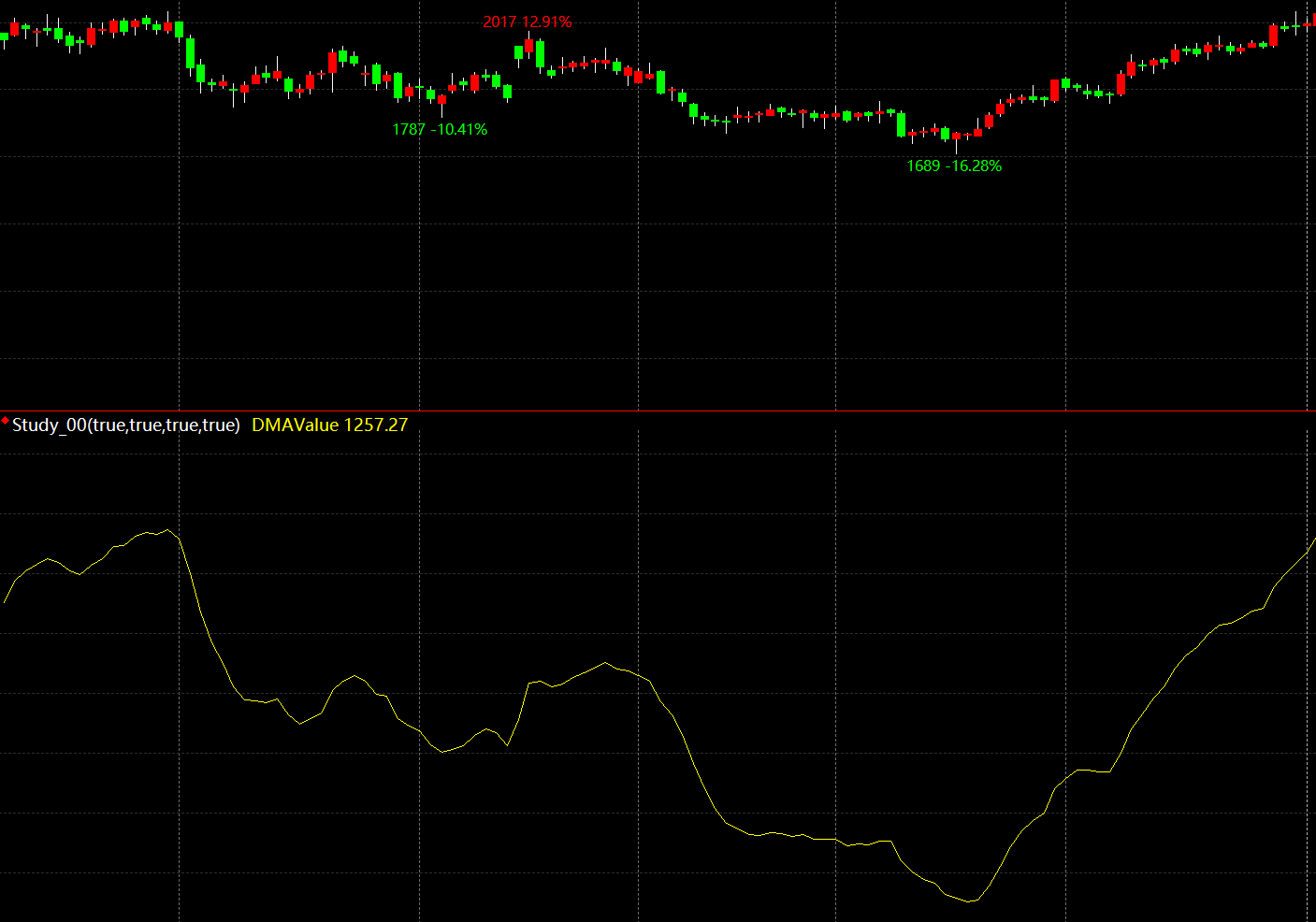
第二步:去除长期趋势
时间序列B = 长期趋势 + 短期波动;这一步是取其中的短期波动用于构建希尔伯特变化。
这里需要保留所需要的短期波动时间序列。后面的希尔伯特变换的数学对象需要是一个窄带随机过程。带有长期趋势的时间序列频带宽度太大,无法满足希尔伯特变换的要求。这也是希尔伯特变化为什么只能做短期择时的本质元音。稳重索索是将通过信号处理中的二阶高通滤波器计算得到去出去时候短期波动时间序列。
二阶高通滤波器的公式如下:
SF(T) = (1-α/2)^2 * (price(T) - 2price(T-1) + price(T-2)) + 2(1-α) * SF(T-1) - (1-α)^2 * SF(T-2)
此时:
T:为时间序列T表示单签时刻,T-1表示回溯上一期一次类推。
ST:为二阶高通滤波器
0<α<1:此处默认为0.25
price:表示为第一步降噪后的长期趋势。
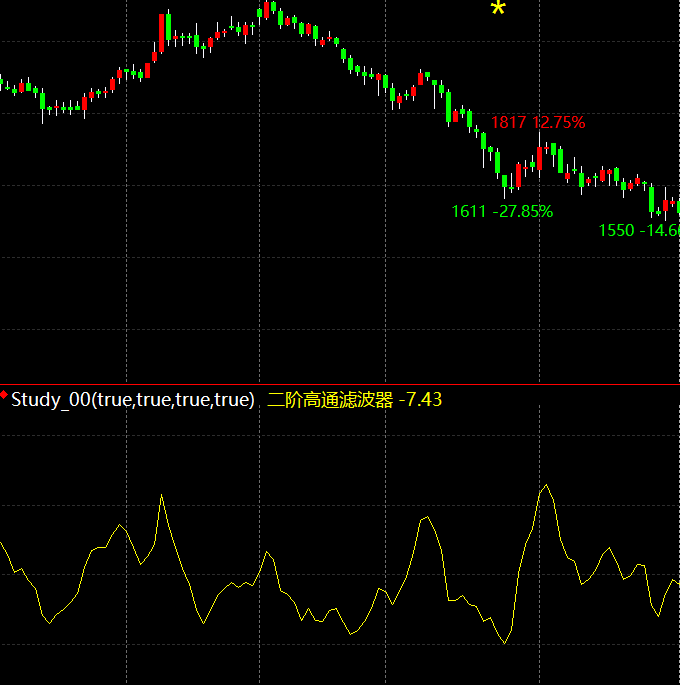
通过公式的计算我们获取短期波动,也就是一个窄带随机过程。
第三步:希尔伯特变换构建同相正交空间
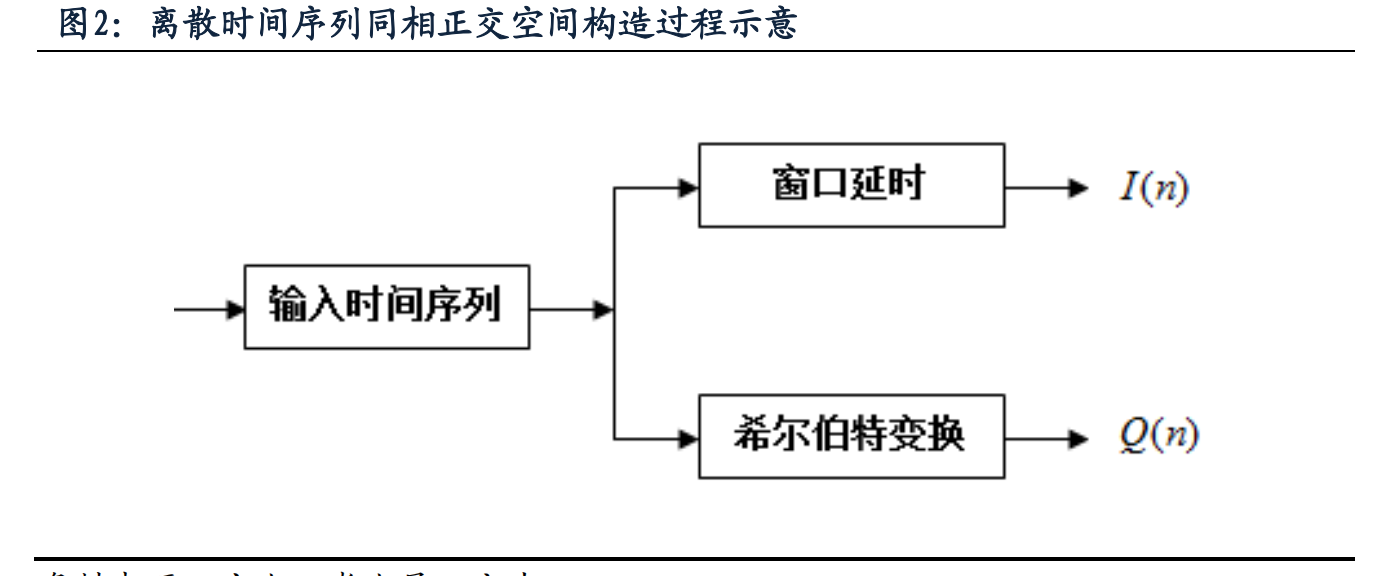
下面来进行希尔伯特变换,具体的希尔伯特变换公式可以参考金工报告,重点是需要进行两个向量的卷积运算。在这里利用TBQuant的强大功能实现希尔伯特变换,在这里主要是为了获得:同相分量(Inphase component)和正交分量(Quadrature Component),下面简称I和Q。再直观点儿说是为了使通过二阶高通滤波器分解的窄带信号映射在复平面空间上,也就是相量空间,如图:
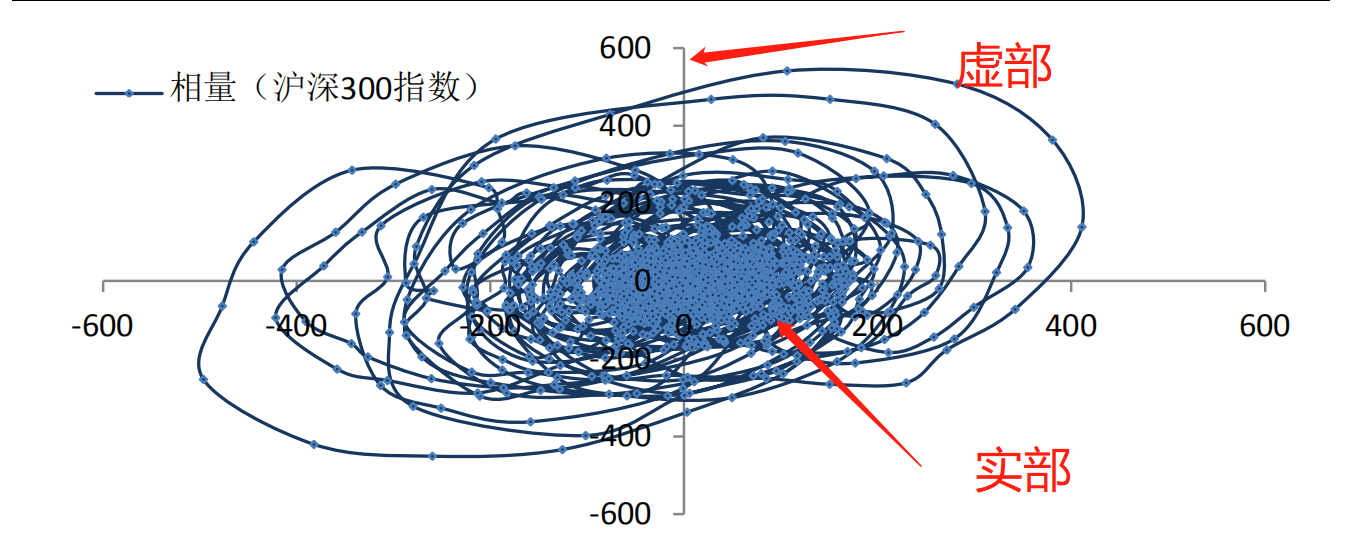
通过TBQuant的希尔伯特变换我们将分解到实部和虚部。Q = 虚部;I = 实部。
分步分解序列入下:
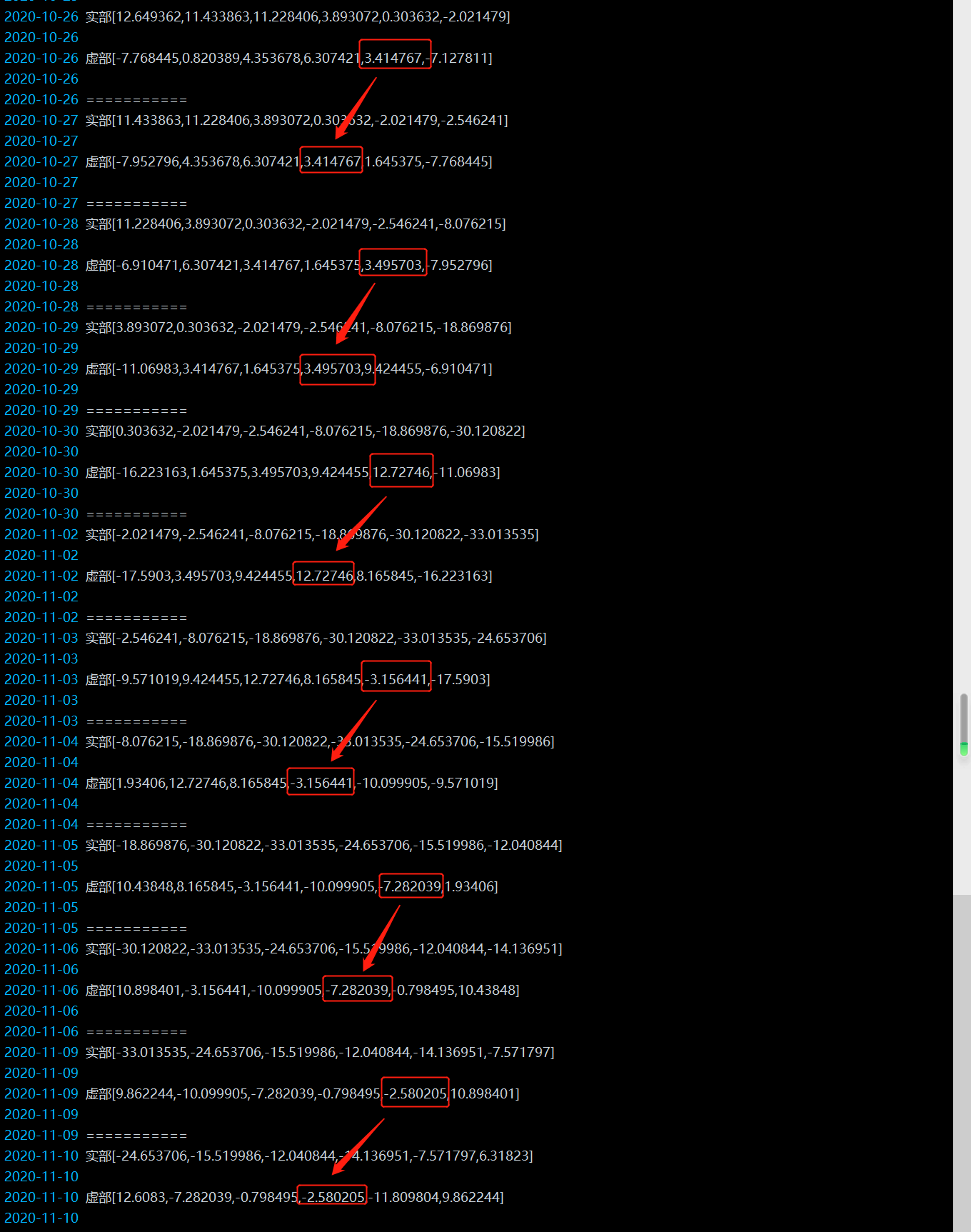
在这里我们采用的是窗口分解方式,数据的取值是随着窗口移动进行的。在这里我们不断取近期最新的5个值。发现这样一个现象,最新分解的虚部最后一个值是变动的且在当期不是固定的(实部一样,因为就是实际的窄带信号值)。我们会看金工报告。

在这里找到出处:希尔伯特变化用到了未来的M时刻的数据点。也就是希尔伯特变化存在M个数据点的数据延迟。在这里表现为下一期。原文是需要对原数据推迟M个时刻,其实在这里可以用回溯的方式也是可以的。不过好处是在这里的当期值用上一期的值,实际交易和计算时并不需要采用回溯的方式了。
我们把实部和虚部分别画出来,也就是I和Q的值。
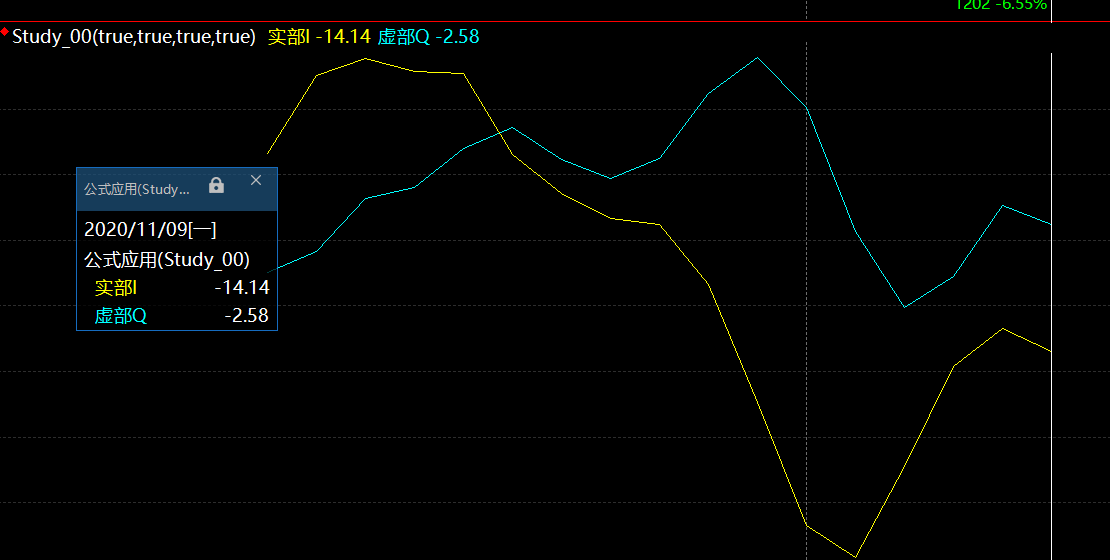
我们这样看的话看不太清楚,其实这就是两点的坐标,分别表示X轴和Y轴,在复平面上表示的是实轴和虚轴。我们把这些点画出来,标准以下他们的走势。分别对应K线的走势。基本上来说表示的是非常对应的关系。“价格运动轨迹”也就是我们所说的相量空间,其实在这里是看的比较清晰,价格是围绕着以0为原点进行逆时针的旋转运动。
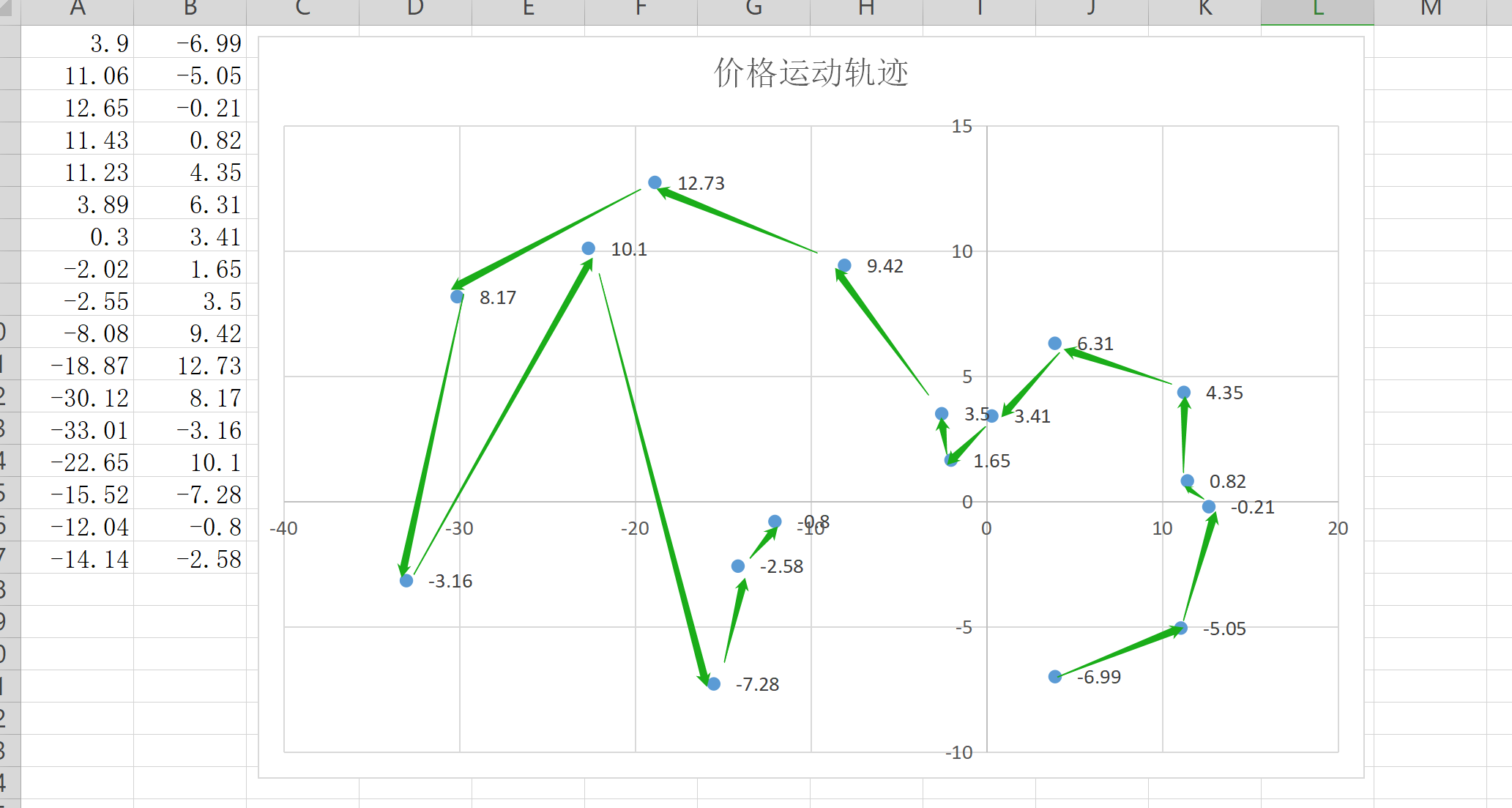

第四步:计算并处理每个时刻的瞬时周期
在上面的就不能中我们已经计算出同相和正交两个变量。在这里我们已经可以得出同相正交空间中所处的位置。其实在上的Excel表格已经画出这些点。I和Q两个值已知的情况下,我们就可以计算出相量的P值。
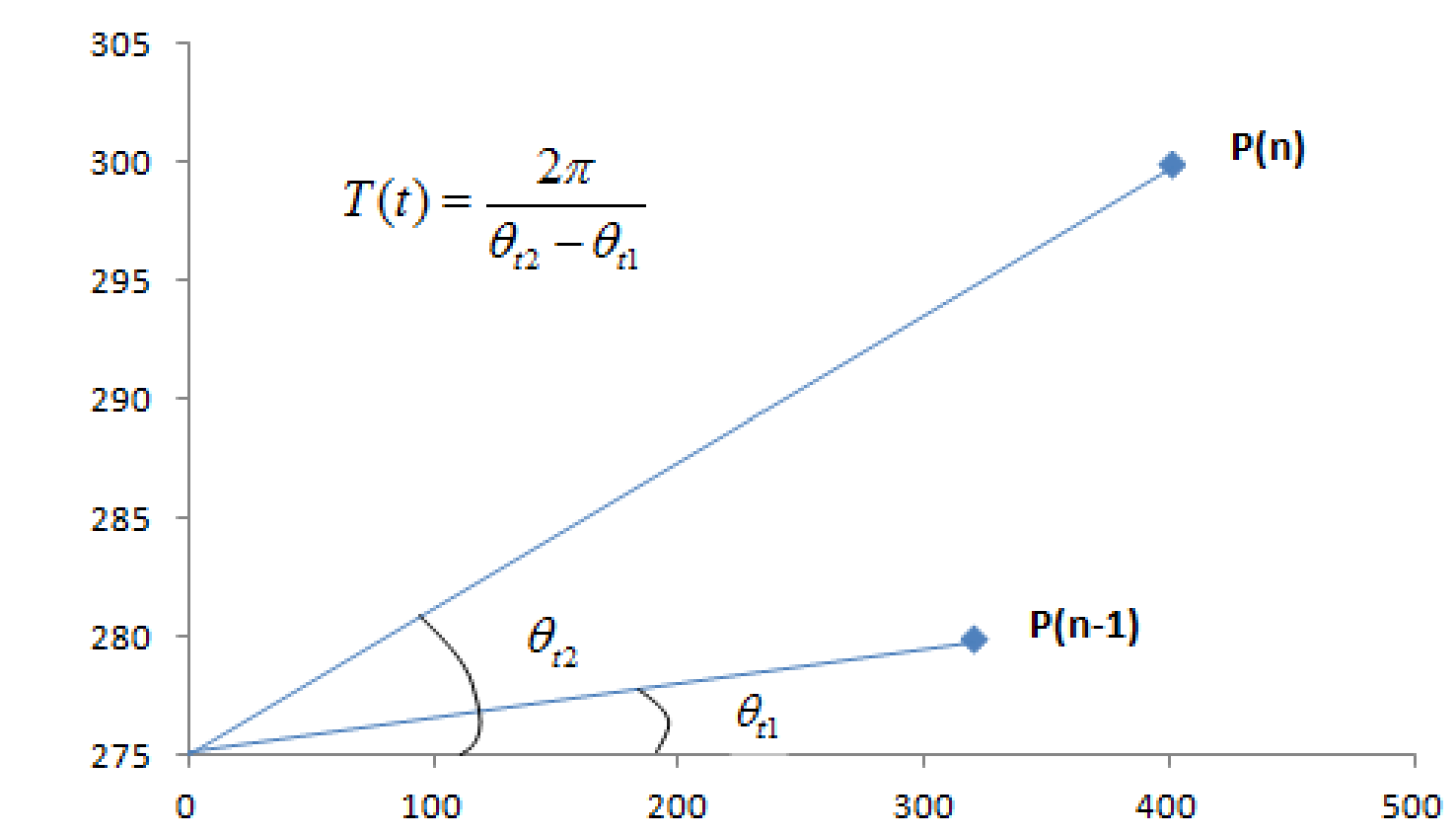
其实在这里的P值就是相量值,也就是上面由I和Q两个点标识出的位置,这个位置也叫做相量值。相量值P可以根据相量的数学表达形式求出:
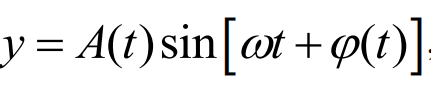
其中A(t)指的是振幅,也是随时间变化的。其实我们并不想求这个值,我们重要的是得到瞬时的动态相交。
第五步:傅里叶变换计算动态相角
动态相交在这类我们定义为θ。这个公式也是非常简单的如下公式。
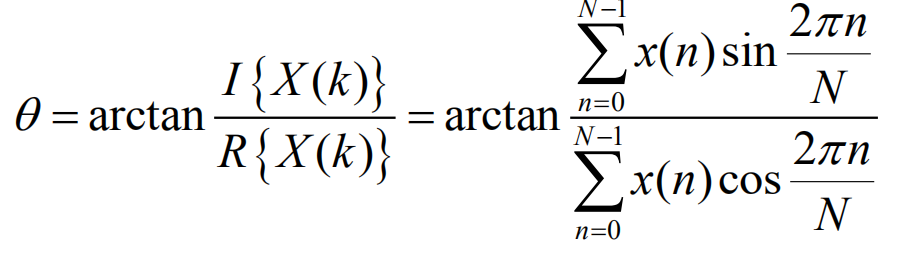
我们只需要用第一个公式即可。分子为虚部I,分母为实部R。然后我们求一个arctan反正切,就能求出瞬时动态的相交,也就是θ。这里求出的θ是为了构建相位和延迟相位,剥离出来的θ是我们最终想要的值。
根据TBQuant,这个值也是非常容易求出的。如下图:

第六步:样本内估计最优相位延迟
第七步:根据相位指标确定多空信号
在这一步我们就求出最终的相位指标,示意图如下:
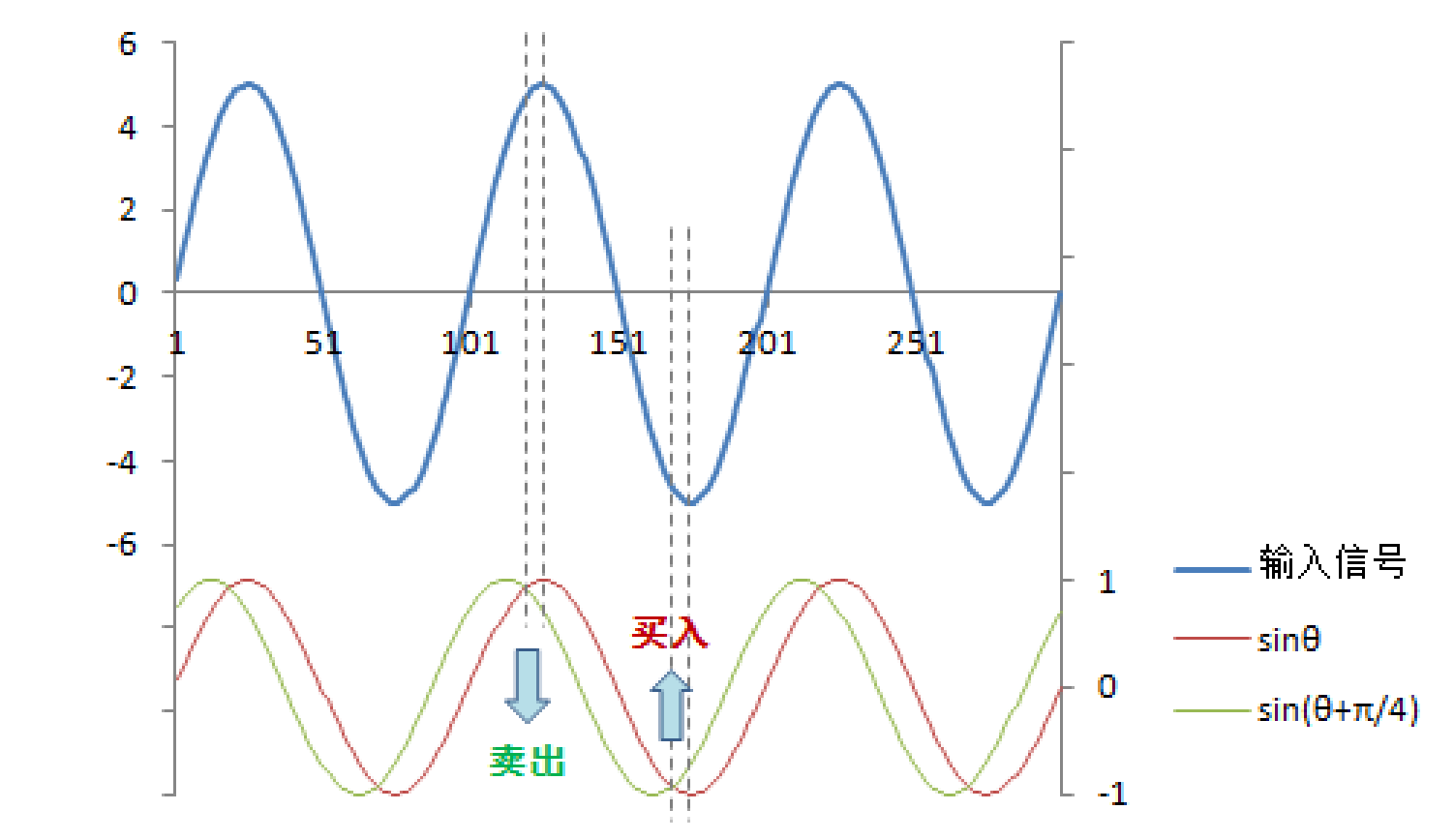
当然,这是一个线性的的表示,实际过程是一个非线性的过程。在这里我们规定两个变量:相位指标(Phase_response)和领先相位(Phase_lead),在这里我们发现延迟相位差一个π/4。
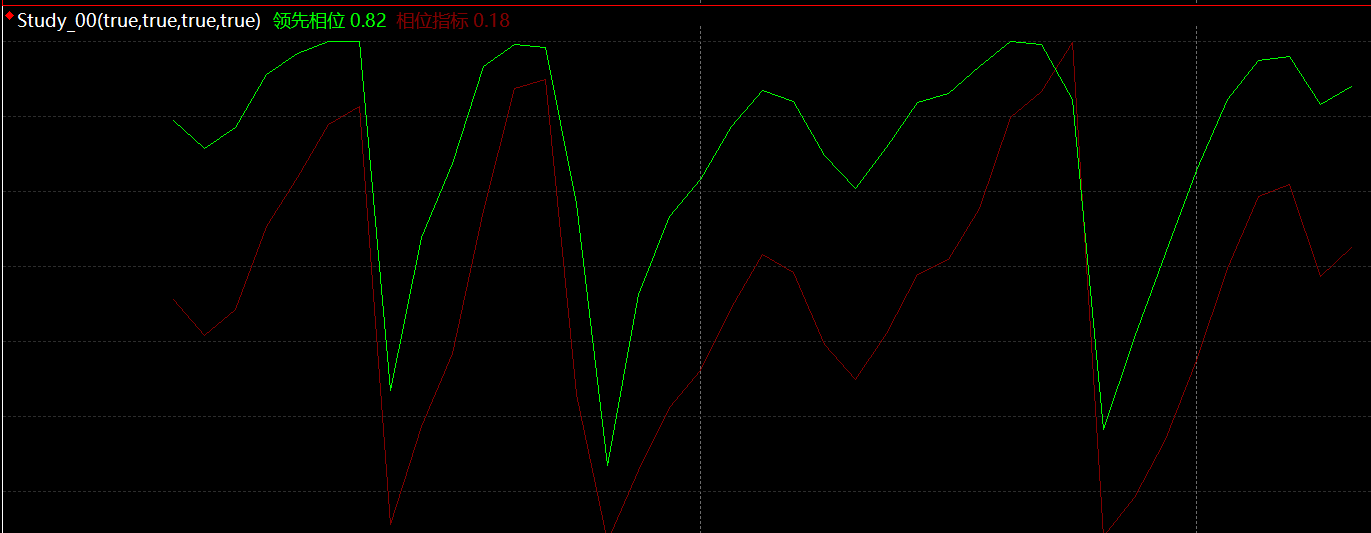
其实这里发现,这些指标并不明显,这是因为我们需要有一个寻优参数,也就是最相位延迟,φ。因此我们的相位指标和领先相位的公式变换为:sin(θ + φ) 和 sin(θ + φ + π/4)。示意图如下:
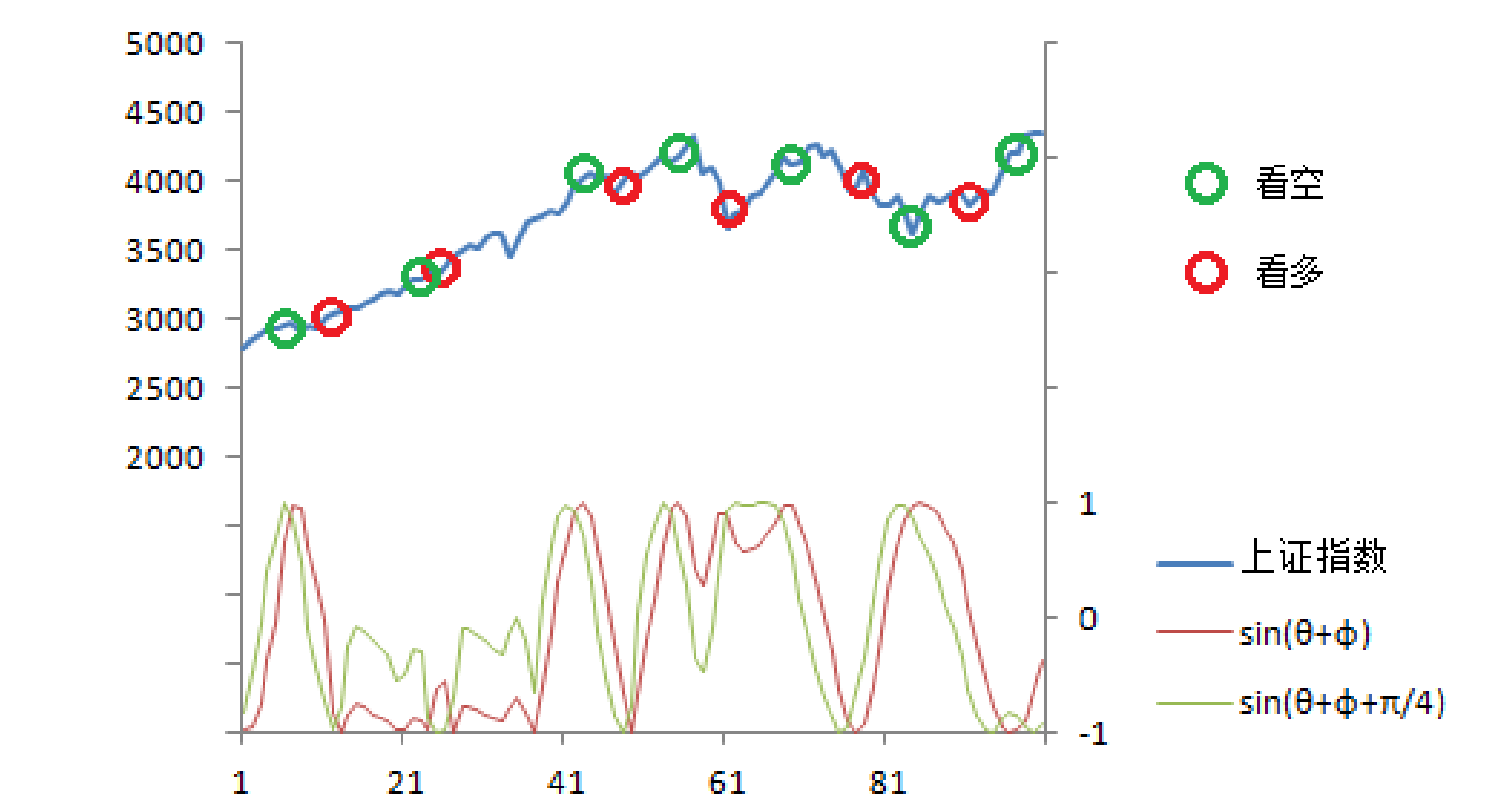
这里有一个问题就是就是φ的取值范围是多少?我们知道一个sin的一个完整的周期是2π(过零点然后再回到0点的位置),九十度为1/2π,负一百八十度为π,负九十度是3/2π,三百六十度为2π,这里就比较容易得到这个φ的取值了。因为在计算的时候我们知道采用的是弧度制,而领先一个完整的周期是360度,我们这里用一个变换取值。这样我们的寻优可以在1~360+的范围取值了。
φ = 角度 ÷ 180 × π
这里寻优参数就是角度。
因此相位指标和领先公式可以变化为如下形式:
integer rad; //角度
Phase_response = sin(θ + rad/180*π) //相位指标
Phase_lead = sin(θ + rad/180*π + π/4 ) //领先指标
相位指标最终结果如下:
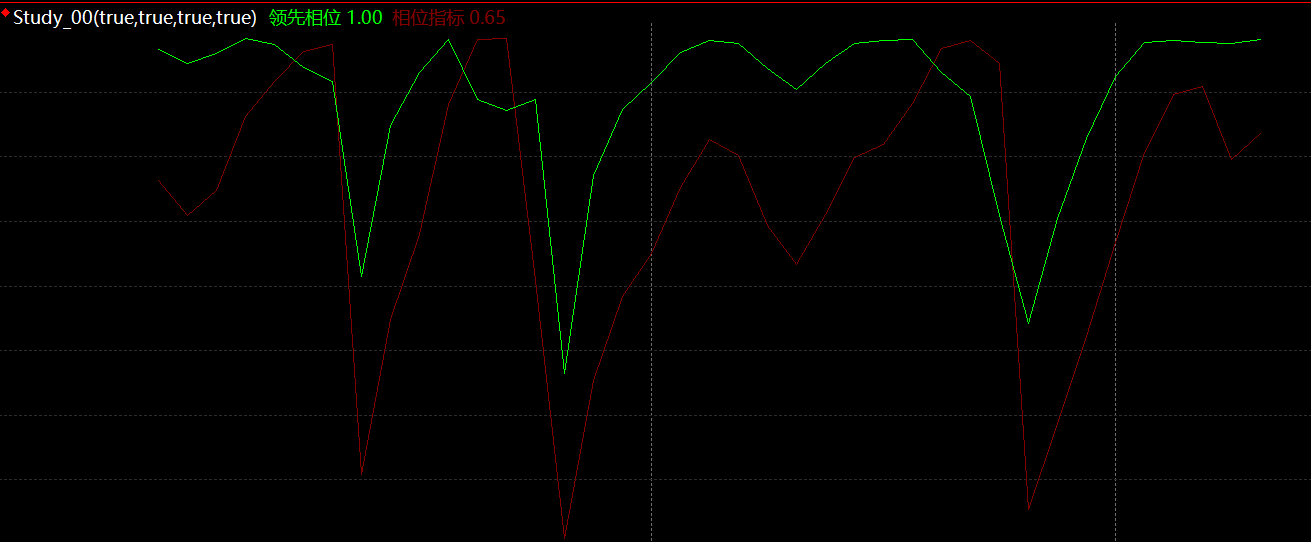

第三章:简单的测试
简单的及交叉策略:
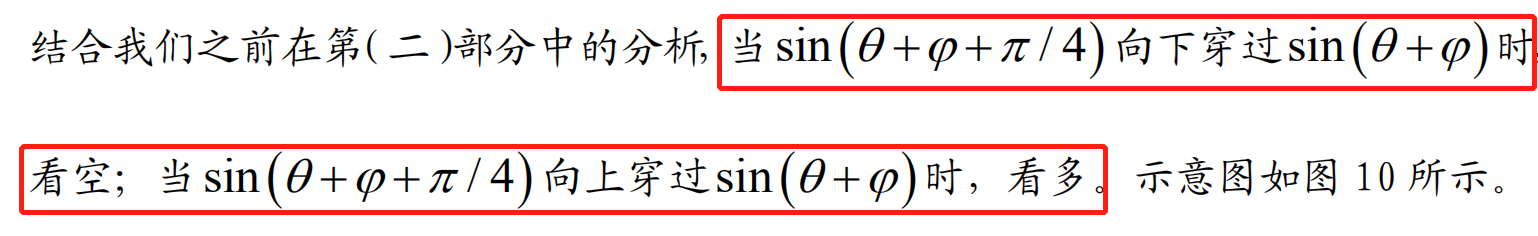
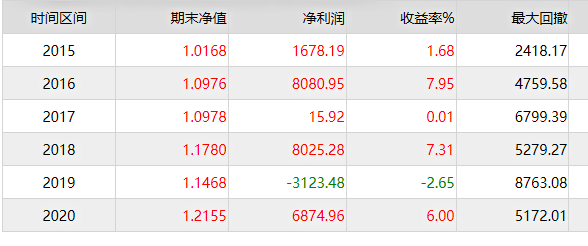
从bu的日线回测结果来看是还可以进行再改进的情况。我们这里设置两个参数,一个是φ最优相位领先,我们在设置会看样本内周期lenght的长度,再来看看,无止损的情况,连续交易状态。
如下是螺纹钢在加1条下最优参数下的结果:
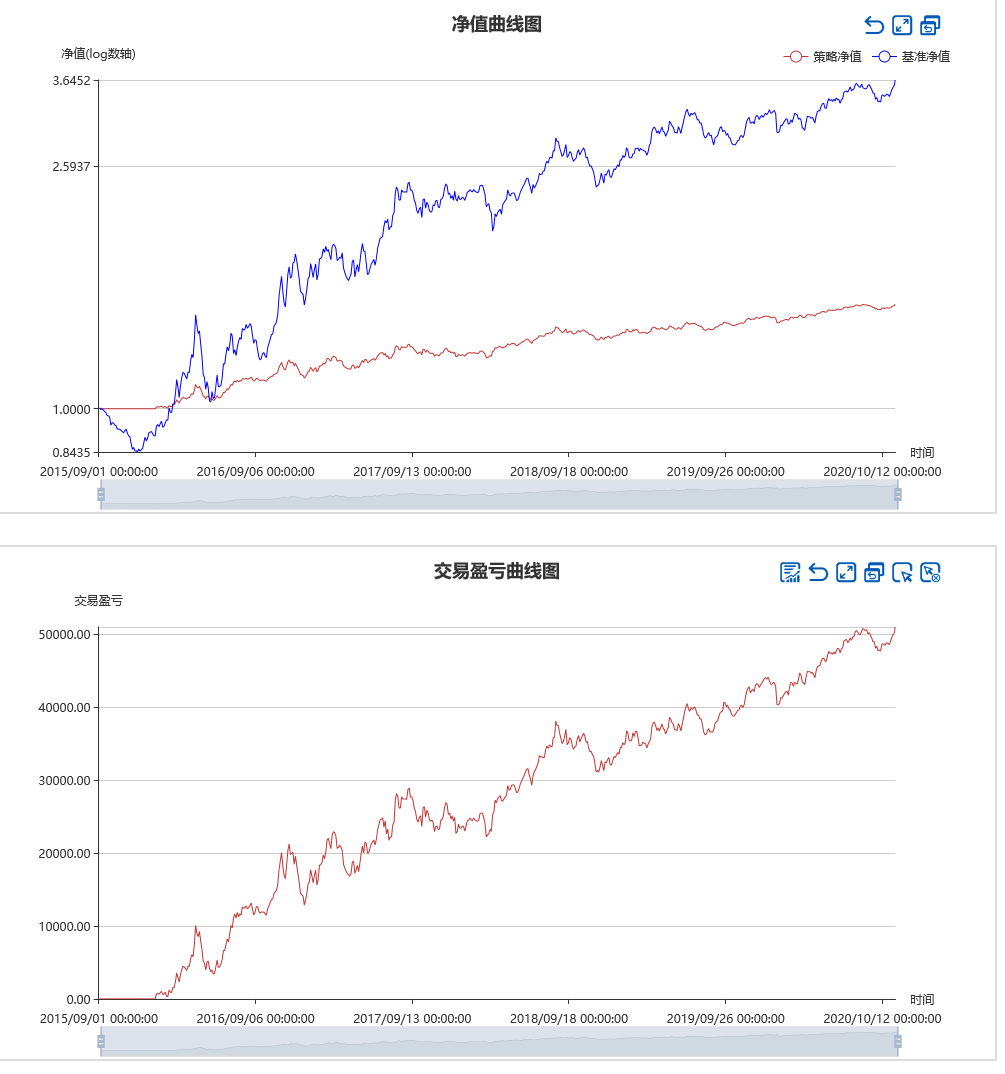
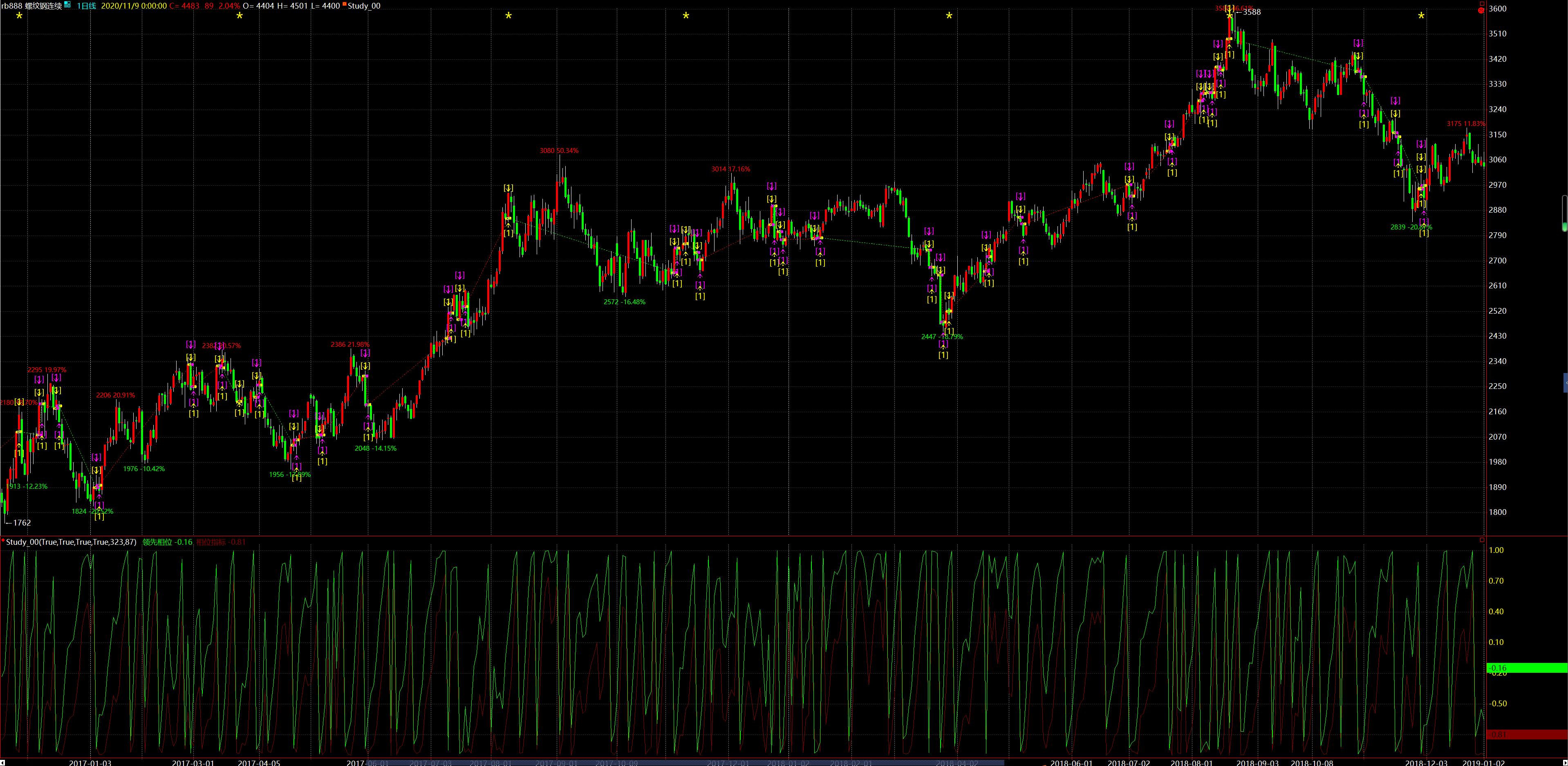
当然,这种连续交易的方式有时也并不可取,不过这个模型是由比较值得开发的潜力。
=================================================
本篇文章借用出处如下:
https://baike.baidu.com/item/%E7%9B%B8%E4%BD%8D/2391710?fr=aladdin
https://www.zhihu.com/question/31104681
之前的文章感谢大家的转载,希望转载时请注明出处,本人转自其它网站的图表一并感谢,谢谢~!
https://www.cnblogs.com/noah0532/
本博客所有文章仅用于学习、研究和交流目的,欢迎非商业性质转载。




