AVL树(Java实现)
AVL树基本介绍
AVL树是一种自平衡的二叉查找树，在AVL树中任何节点的两个子树的高度差不能超过1。就是相当于在二叉搜索树的基础上，在插入和删除时进行了平衡处理。
不平衡的四种情况
LL：结构介绍
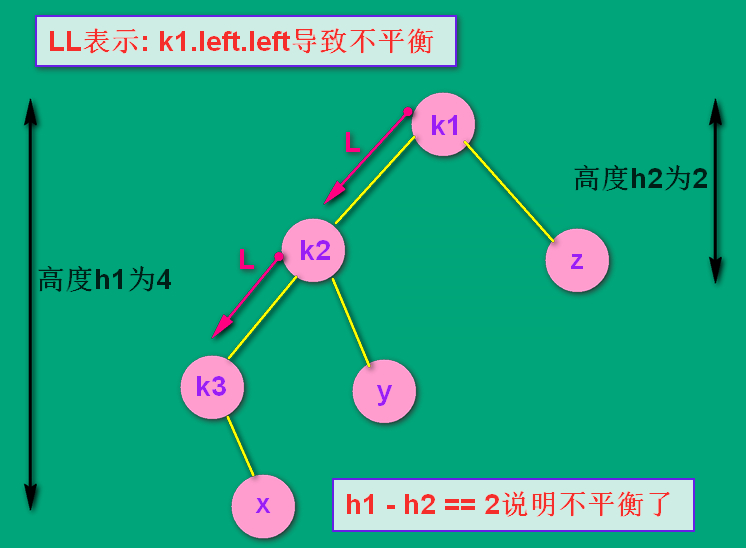
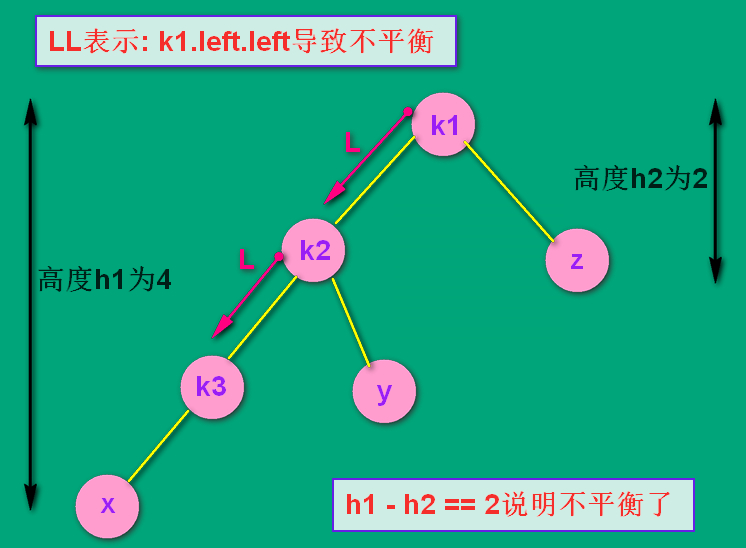
看如下图，假设最初只有k1, k2, k3, y, z 五个结点，这时该树两边的高度分别为3 和 2，相差为1，满足AVL平衡的概念。
随后插入了结点 x ，导致了不平衡。k1.left.left 有了子树，导致了不平衡。所以是LL结构。
（这个 x 结点是k3的左孩子还是右孩子无所谓,因为无论在左还是在右，处理的方式是通用的）
LL：处理
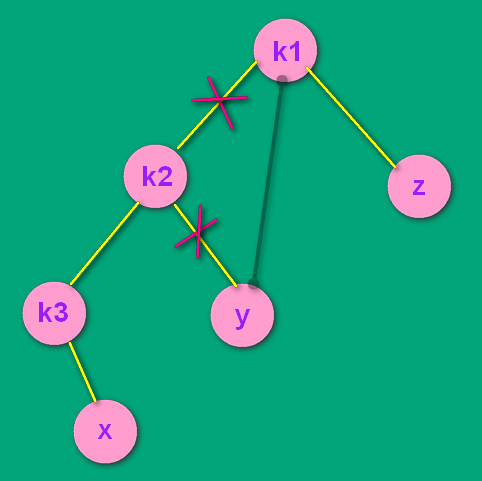
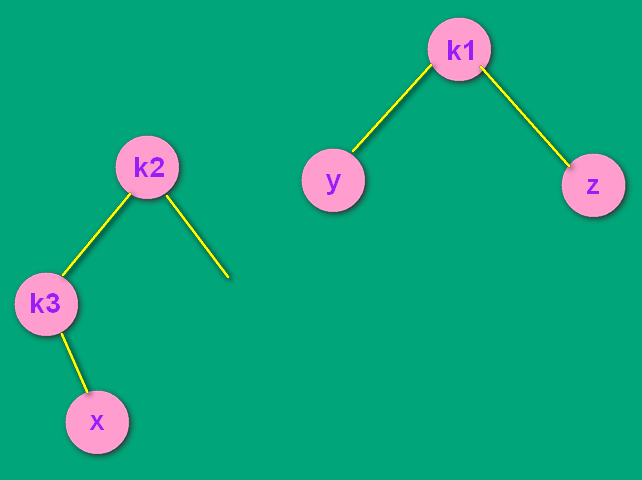
调整的时候发现，k3 和 x 的相对连接关系一直没变，所以x是k3的左孩子还是右孩子无所谓了,都是LL处理方式。x 如果是 k3 的左孩子，处理方式和步骤一模一样。
---> 
---> 
--->
--->
---> 
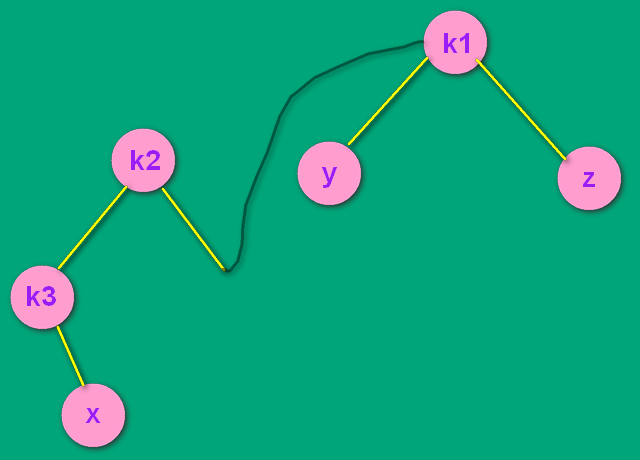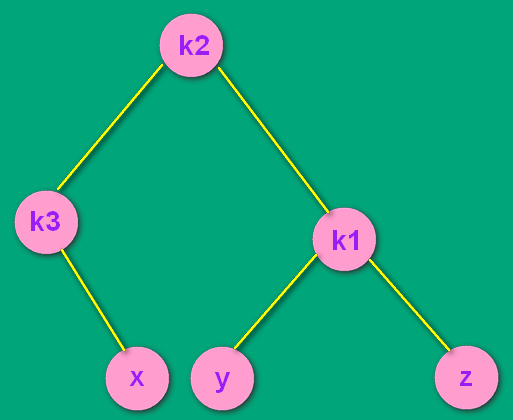
LL：代码
/**
* @param k1 k1结点的左右两边的高度差2
* @return 返回LL单转后的新根k2
*/
private Node leftLeftRotation(Node k1) {
Node k2 = k1.left;
k1.left = k2.right;
k2.right = k1;
k1.height = max(height(k1.left), height(k1.right)) + 1;
k2.height = max(height(k2.left), k1.height) + 1;
return k2;
}
RR：结构介绍
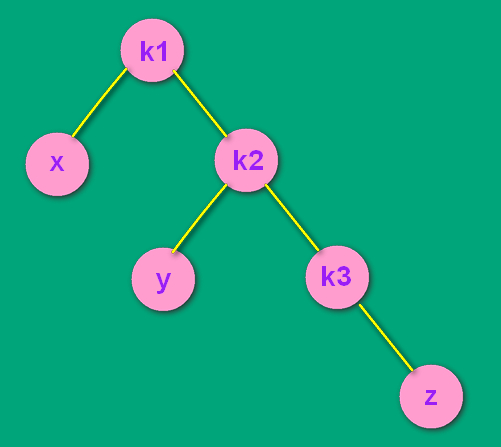
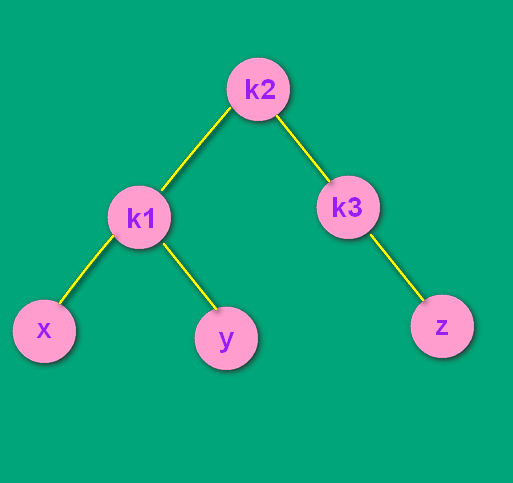
看如下图，假设最初只有k1, k2, k3, x, y 五个结点，这时该树两边的高度分别为2 和 3，相差为1，满足AVL平衡的概念。
随后插入了结点 z ，导致了不平衡。是 k1.right.right 有了子树，导致了不平衡。所以是RR结构。
（这个 z 结点是k3的左孩子还是右孩子无所谓,因为无论在左还是在右，处理的方式是通用的）
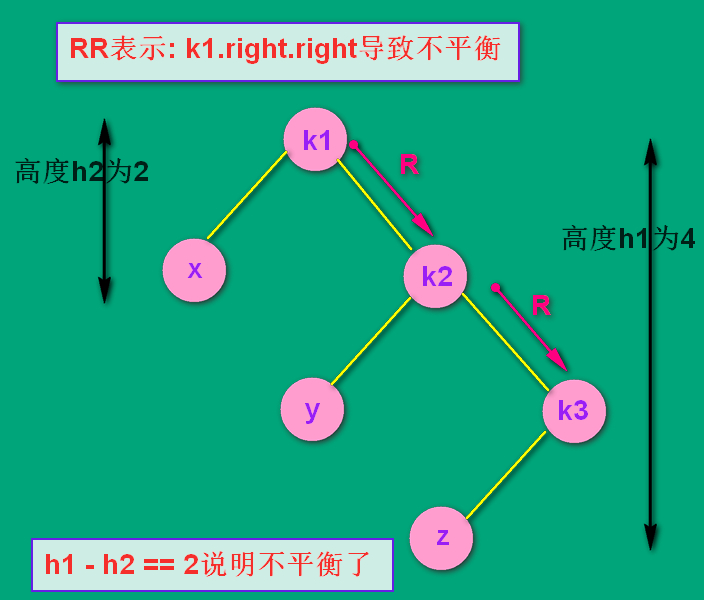
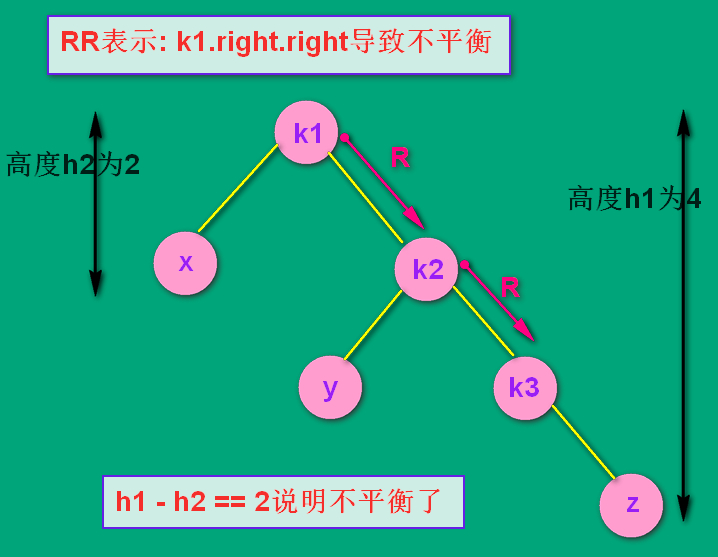
RR：处理
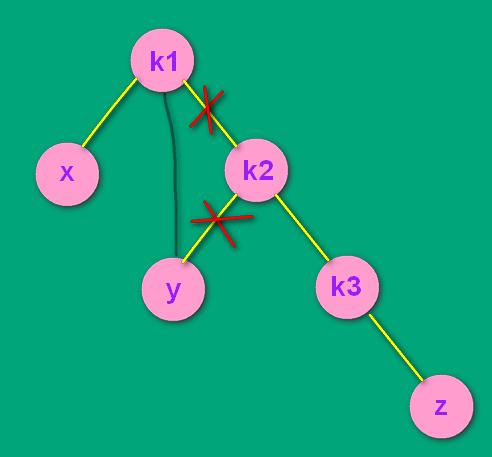
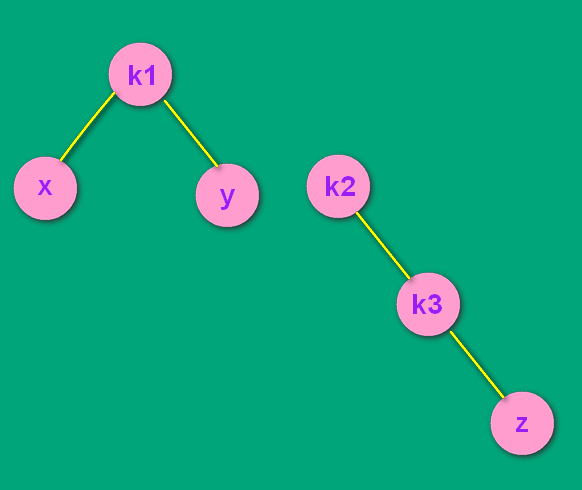
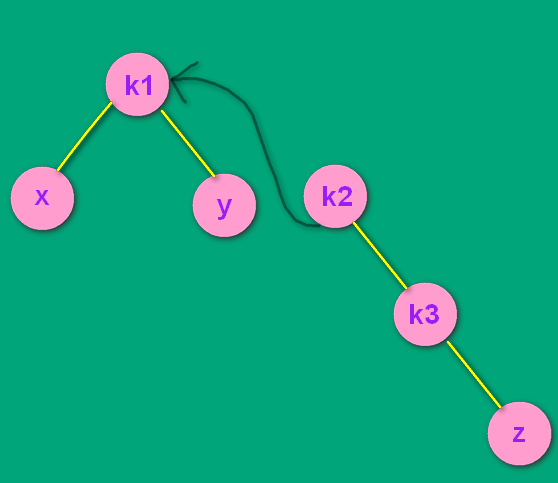
调整的时候发现，k3 和 z 一直没动，所以 z 是 k3 的左孩子还是右孩子无所谓了,都是 RR 处理方式。z 如果是 k3 的左孩子，处理方式和步骤一模一样。
--->
--->
--->
--->
--->
RR：代码
/**
* @param k1 k1结点的左右两边的高度差2
* @return 返回RR单转后的新根k2
*/
private Node rightRightRotation(Node k1) {
Node k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max(height(k1.left), height(k1.right)) + 1;
k2.height = max(k1.height, height(k2.right)) + 1;
return k2;
}
LR：结构介绍
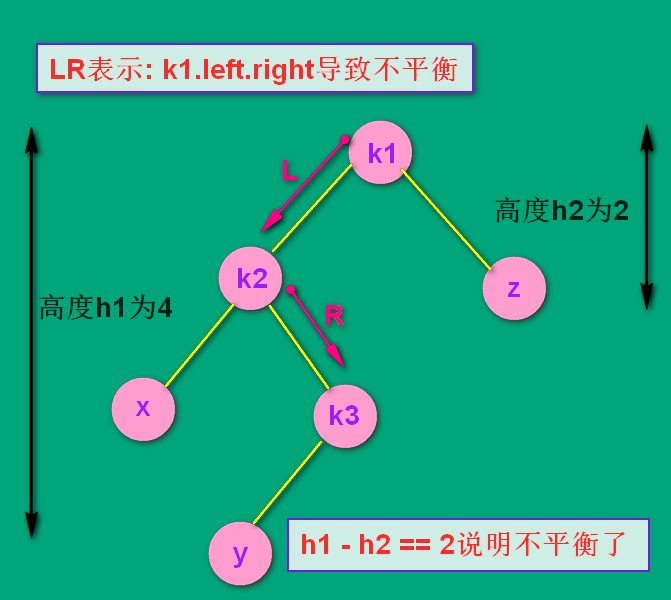
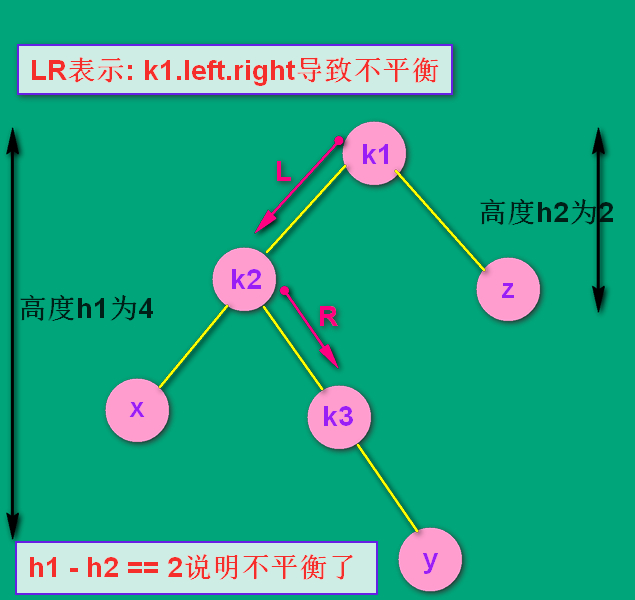
看如下图，假设最初只有k1, k2, k3, x, z 五个结点，这时该树两边的高度分别为3 和 2，相差为1，满足AVL平衡的概念。
随后插入了结点 y ，导致了不平衡。是 k1.left.right 有了子树，导致了不平衡。所以是LR结构。
（这个 y 结点是k3的左孩子还是右孩子无所谓,因为无论在左还是在右，处理的方式是通用的）
LR：处理
为了后面更方便地描述，我把k3的右孩子 null 空指针画了出来。
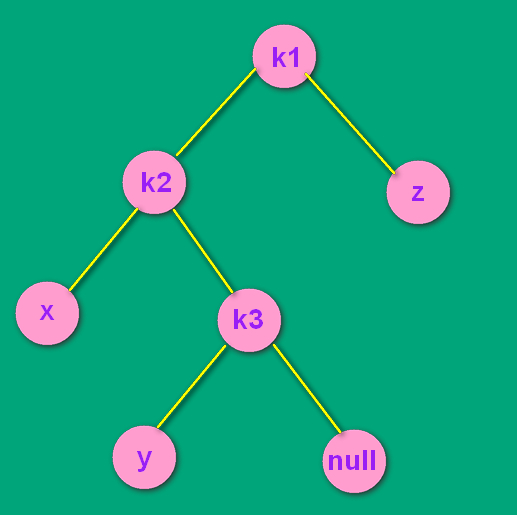
现在是LR结构。
先不看k1 和 z 两个结点，把 k1 和 k2 断开连接。把k2为根的子树当成RR结构来进行处理。即先处理这个'R'
--->
---> 
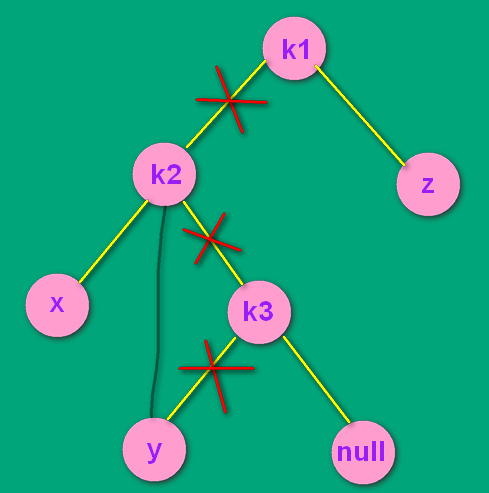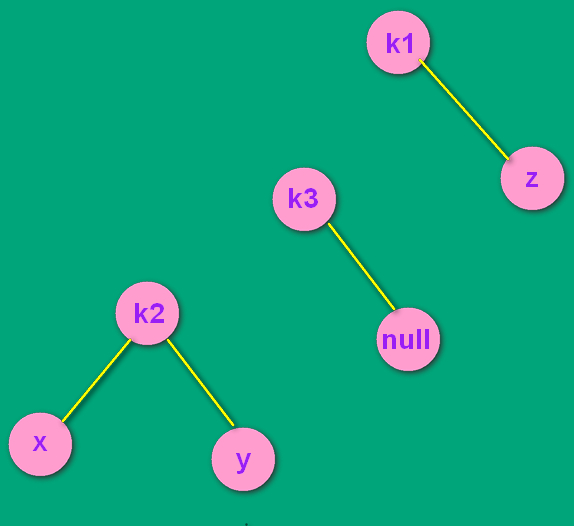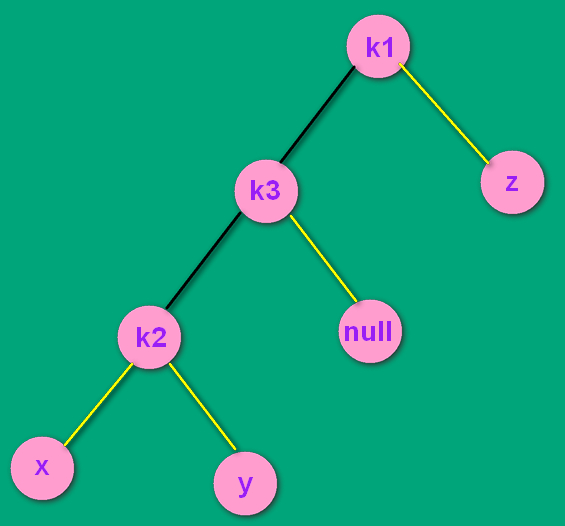
如上面最后一张图,经过了RR单转之后，变成了LL结构。对k1为根的树其进行LL单转。如下所示：
--->
--->
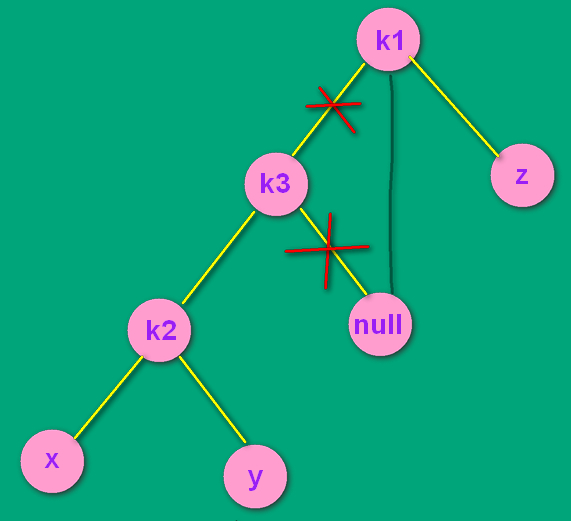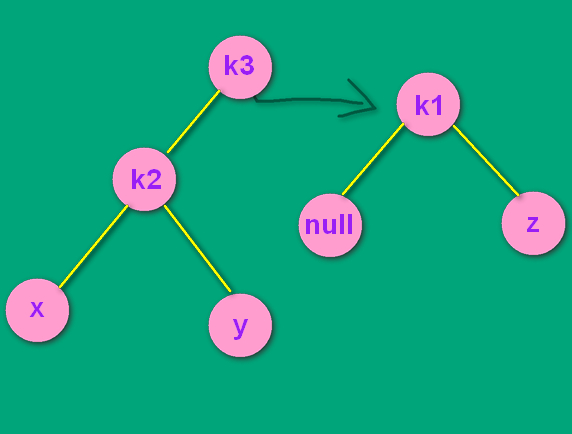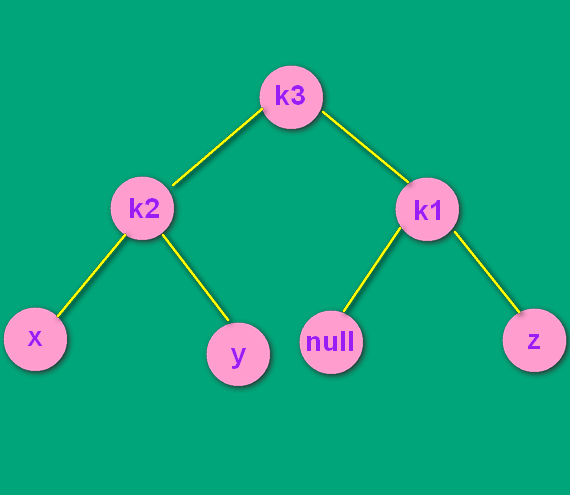
本次我只演示了当 y 是k3的左孩子时的情况。如果y插入时,是k3的右孩子,那其实就是图片中null结点的地方。转换方式是一模一样。
LR：代码
发现LL 和 RR写好以后，LR虽然复杂，但直接调用这两个方法就行了。很短的。
/**
* @param k1 k1结点的左右两边的高度差2
* @return 返回LR单转后的新根k2
*/
private Node leftRightRotation(Node k1) {
k1.left = rightRightRotation(k1.left);
return leftLeftRotation(k1);
}
RL：结构介绍
看如下图，假设最初只有k1, k2, k3, x, z 五个结点，这时该树两边的高度分别为2 和 3，相差为1，满足AVL平衡的概念。
随后插入了结点 y ，导致了不平衡。是 k1.right.left 有了子树，导致了不平衡。所以是RL结构。
（这个 y 结点是k3的左孩子还是右孩子无所谓,因为无论在左还是在右，处理的方式是通用的）
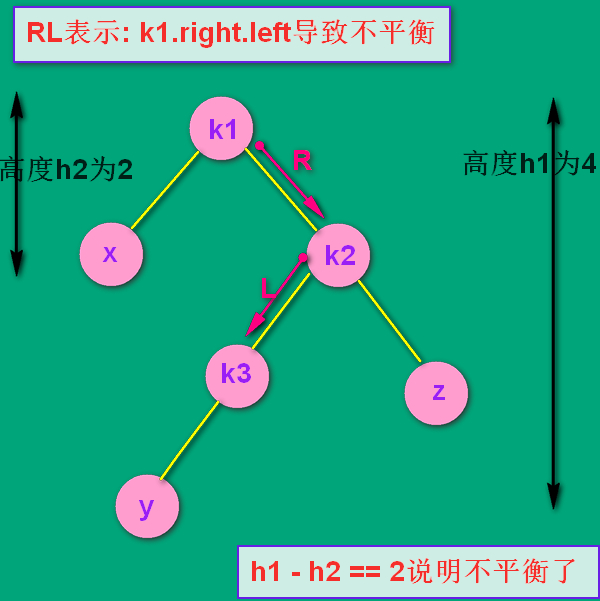
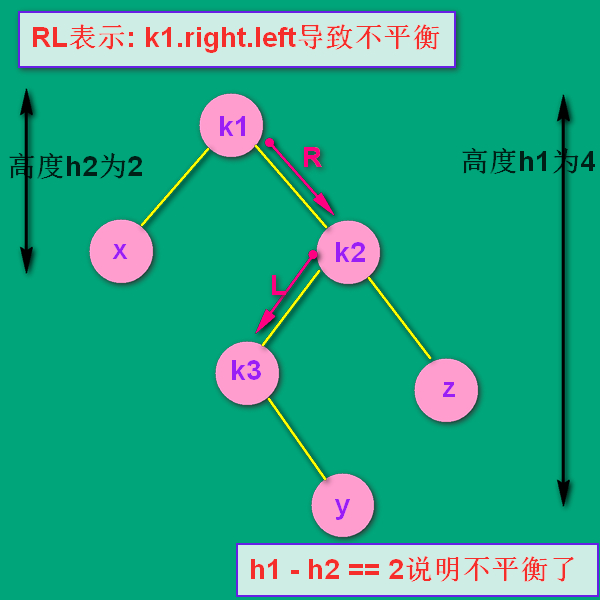
RL：处理
为了后面更方便地描述，我把k3的右孩子 null 空指针画了出来。
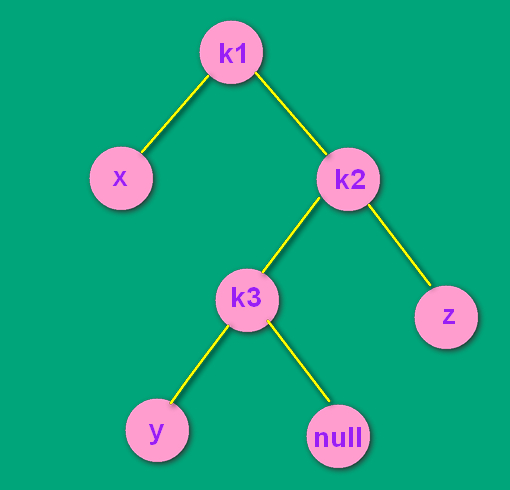
现在是RL结构。
先不看k1 和 x 两个结点，把 k1 和 k2 断开连接。把k2为根的子树当成LL结构来进行处理。即先处理这个'L'
->
->
->
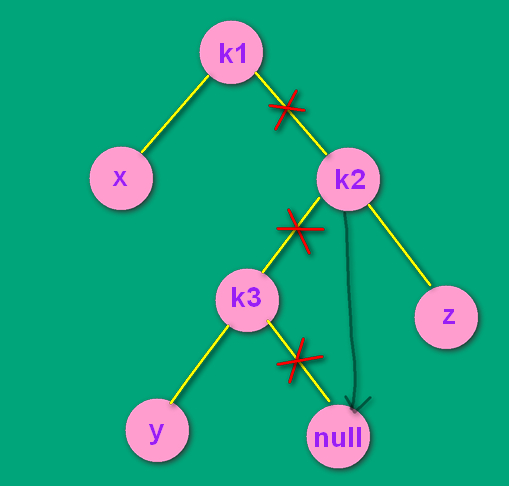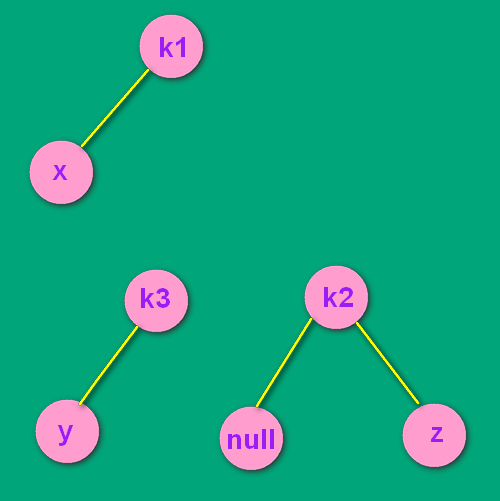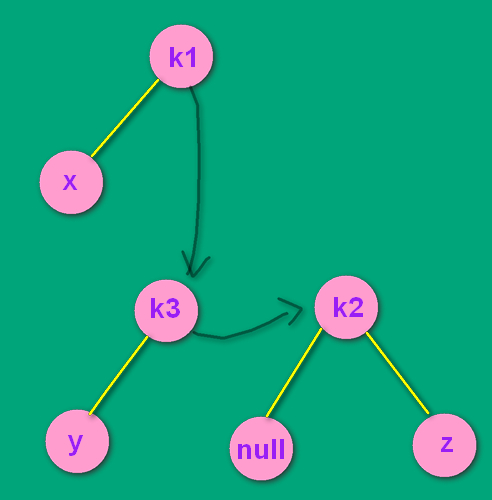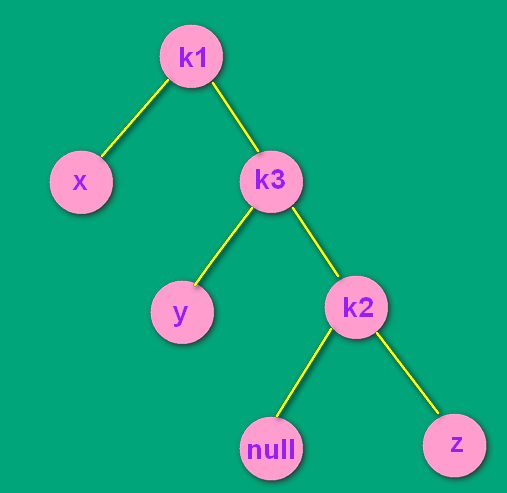
如上面最后一张图,经过了RR单转之后，变成了RR结构。对k1为根的树其进行RR单转。如下所示：
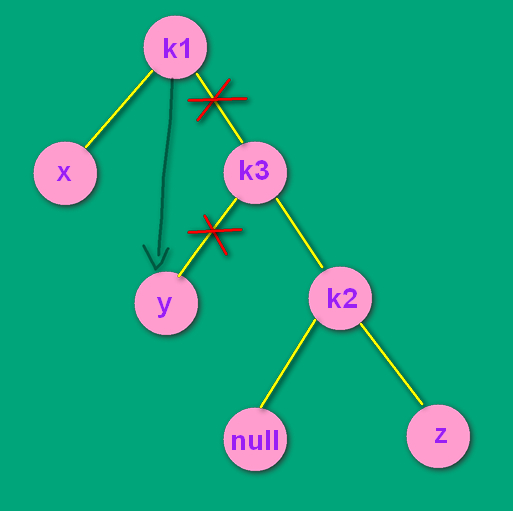
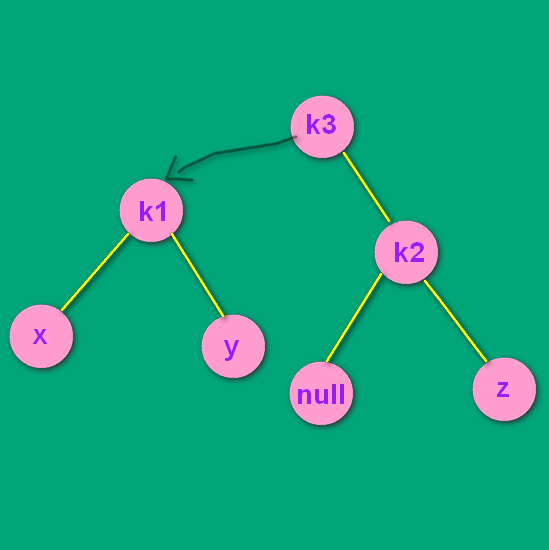
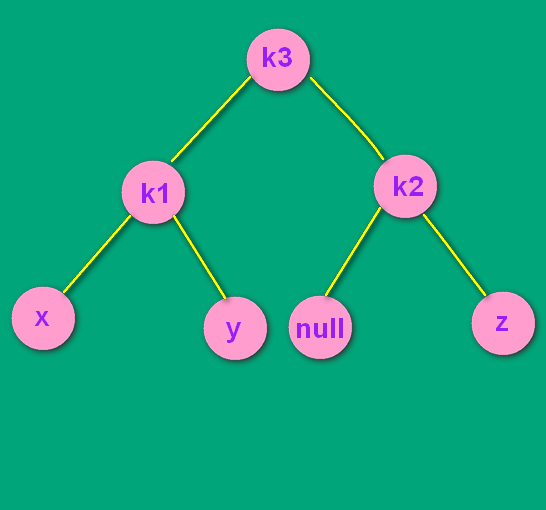
本次我只演示了当 y 是k3的左孩子时的情况。如果y插入时,是k3的右孩子,那其实就是图片中null结点的地方。转换方式是一模一样。
RL：代码
/**
* @param k1 k1结点的左右两边的高度差2
* @return 返回RL单转后的新根k2
*/
private Node rightLeftRotation(Node k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
具体讲解插入导致的不平衡
咱们假设AVL树的初始状态如下，
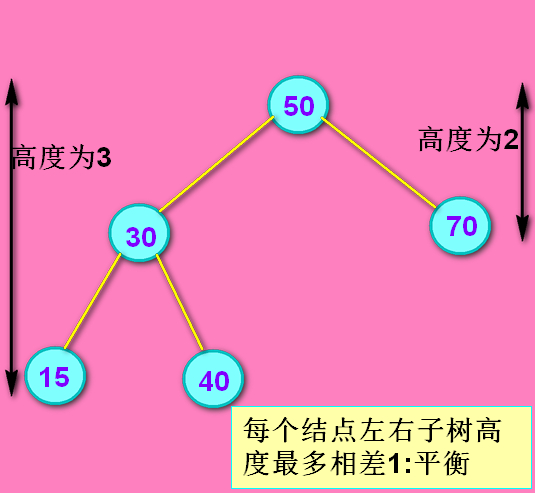
随后插入了一个新的结点7。7与根进行比较，发现7<50，所以去左子树查找。
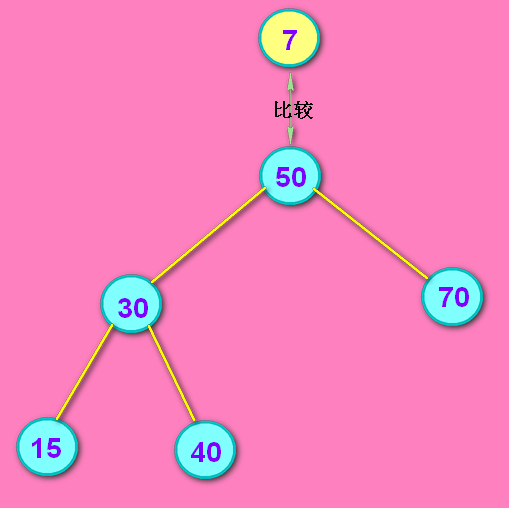
7继续进行比较，7<30，所以继续去左子树查找。
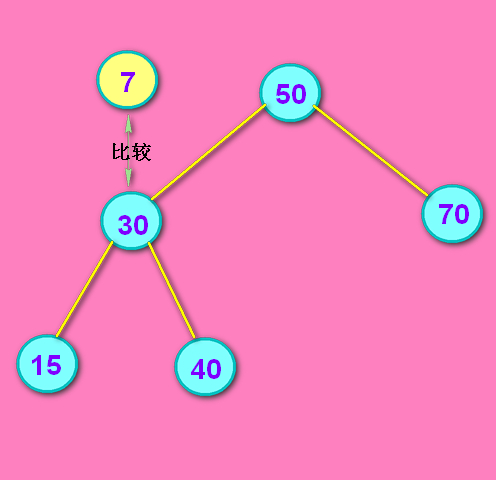
重复这些步骤，在代码里是用递归处理的。直到找到7为止，或者遍历到叶子节点了也没找到7为止。
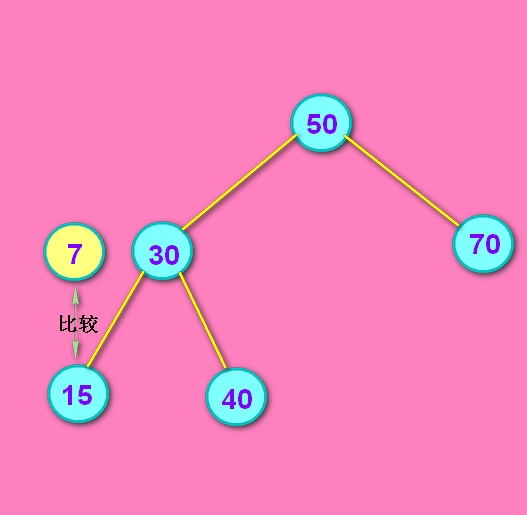
没找到7...因为7比15小，所以7插入在15左侧。这时以k1为根的树不平衡了！！！
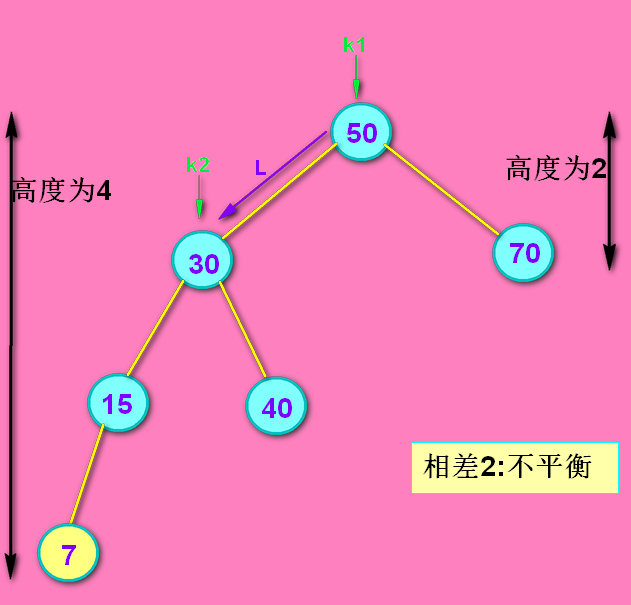
问：我能用眼睛看出来，但程序怎么算呢？ 答：height(k1.left) - height(k1.right) == 2 了。
问：为什么是左子树高度 减 右子树高度？ 答：因为...之前是平衡的，在左侧插入后就不平衡了。肯定是左侧大啊。
问：嗯，左子树高度比右子树大说明啥？ 答：说明...肯定是 k1 左边。也就是LL结构或者是LR结构,第一个字母 ‘L’ 已经确定了。
问：那剩下的你怎么确定是LL还是LR ？ 答：很简单，新节点比k2小，那就是LL；新节点比k2大，那就是LR。继续往下看图：
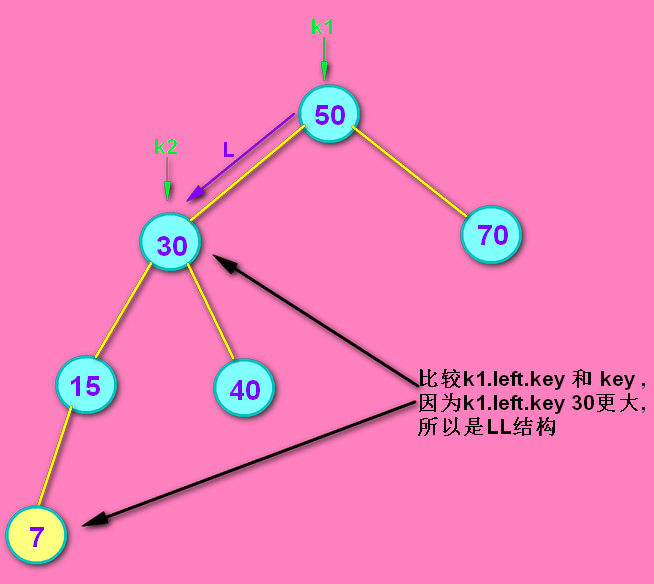---确定了LL结构--->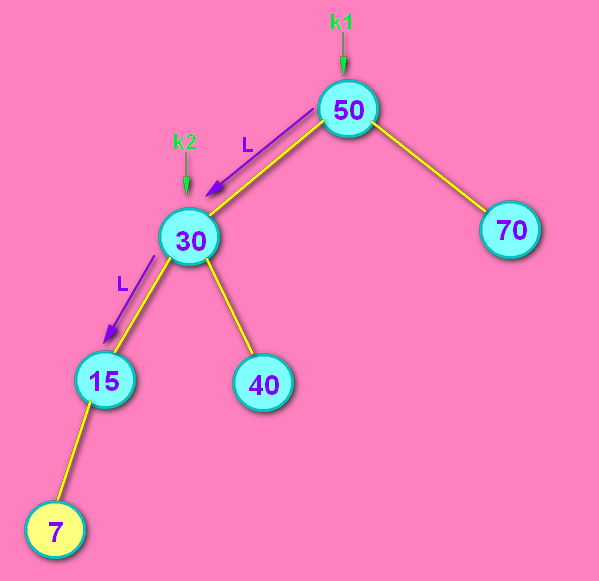
问：LL结构挺好理解，判断LR会不会很麻烦啊？ 答：方法一模一样...没多没少...咱们假设一开始插入的不是7，而是35，那么如下图所示：
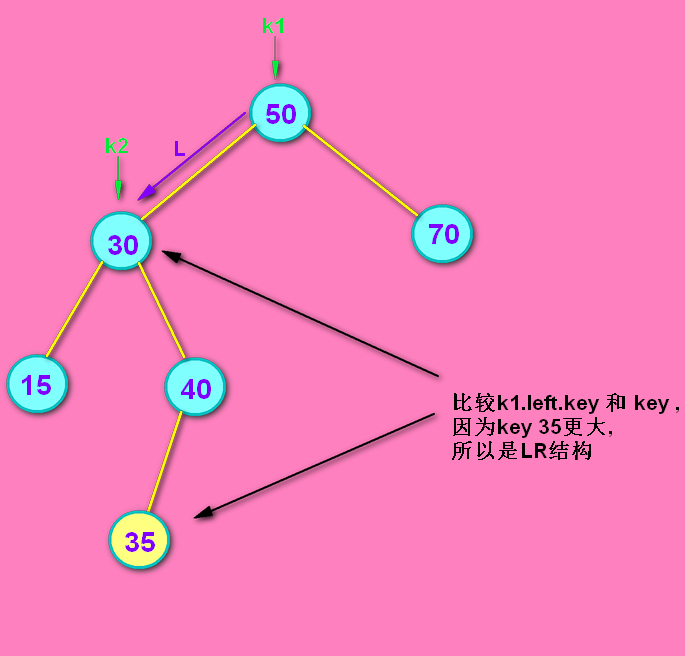---确定LR--->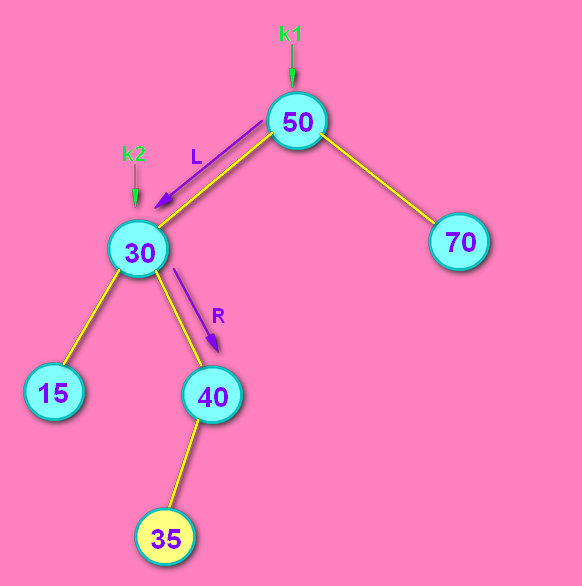
问：为什么不介绍RR和RL了？ 答：LL、LR都会了，RR、RL其实就是一码事了。不再重复演示了.....（画图好累....）
具体讲解删除导致的不平衡
讲删除导致不平衡之前，先讲讲到底怎么在AVL树中删除一个结点。
假设删除前的树如下图所示，想要删除 90 结点：
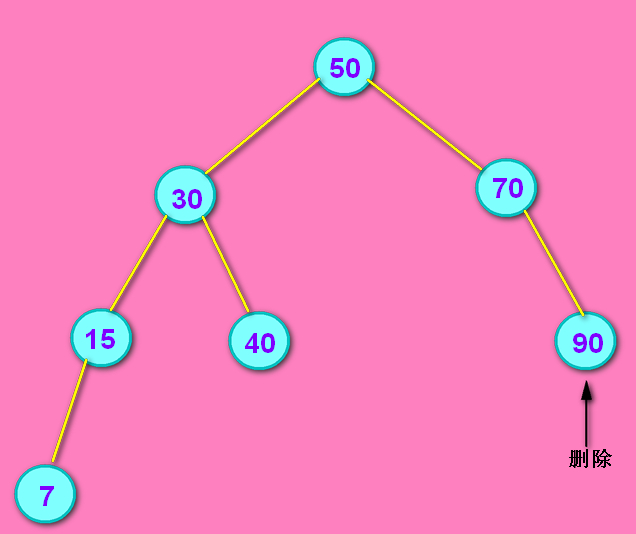
问：怎么删除呢？ 答：先从树根定位到 90 结点。
问：怎么定位呢？ 答：利用递归，与当前子树根进行比较。小，去左边找；大，去右边找；等于，就找到了。
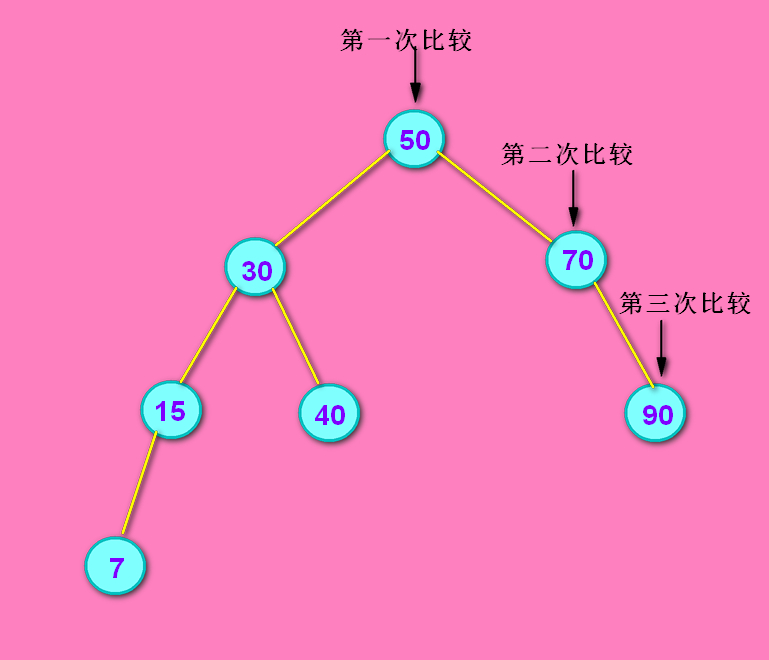
问：找到之后就可以直接删了吗？ 答：还得考虑要删除的那个结点是否还有孩子。分为如下三种情况：
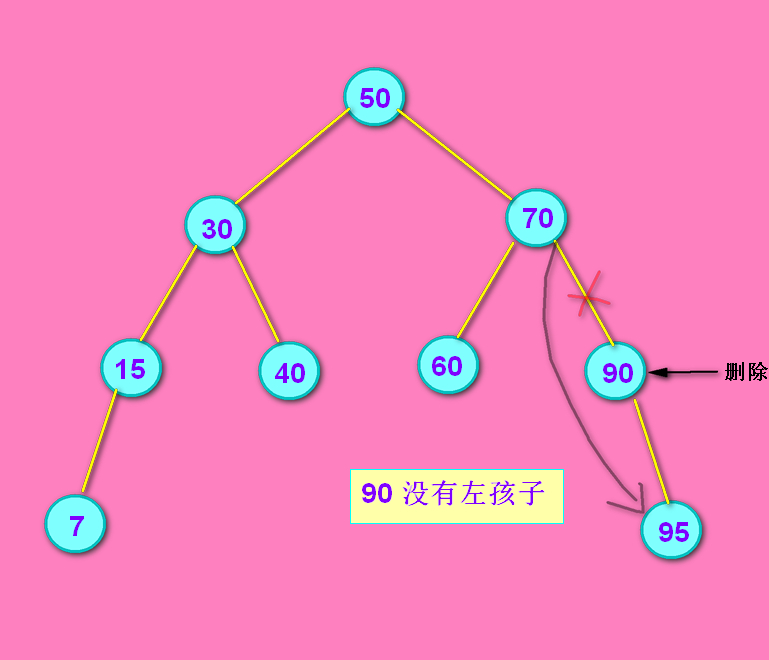
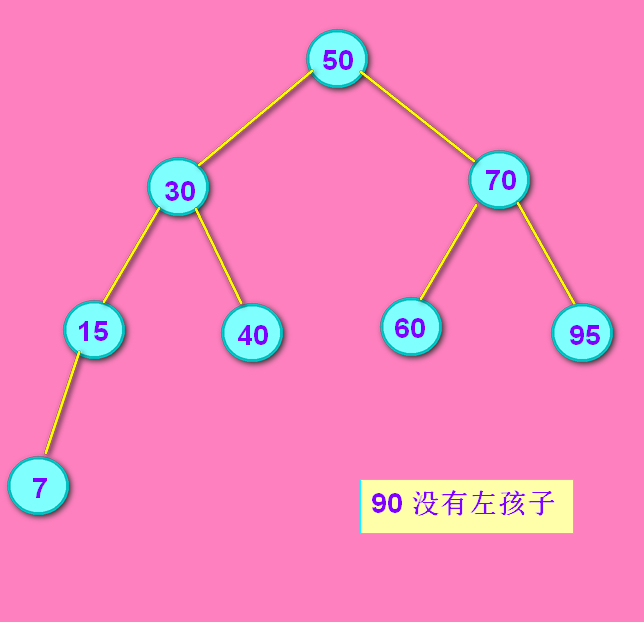
情况1： 90结点没有左孩子
没有左孩子的话，把70结点的right 连上 90结点的right。没有左孩子不代表一定有右孩子。如果90的right是null的话，那就把这个null赋给70的right就好了。
->
->
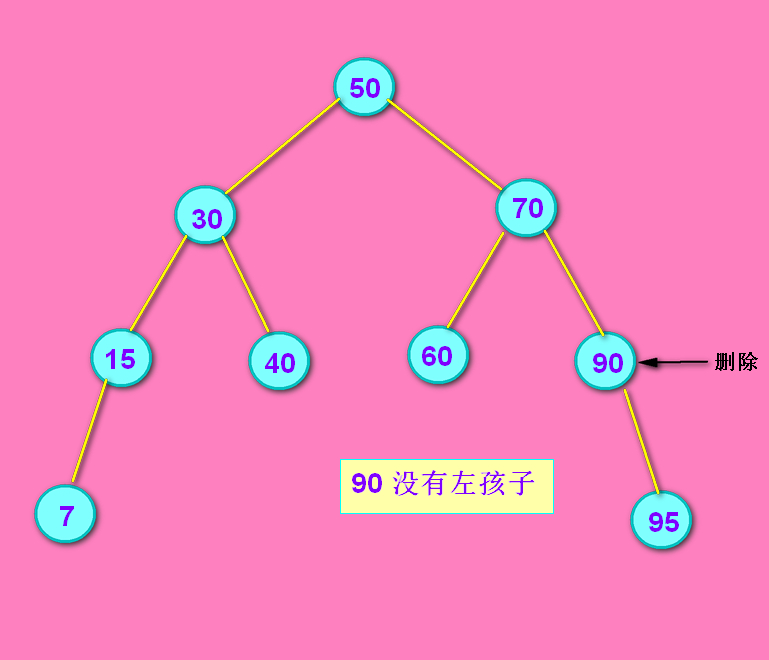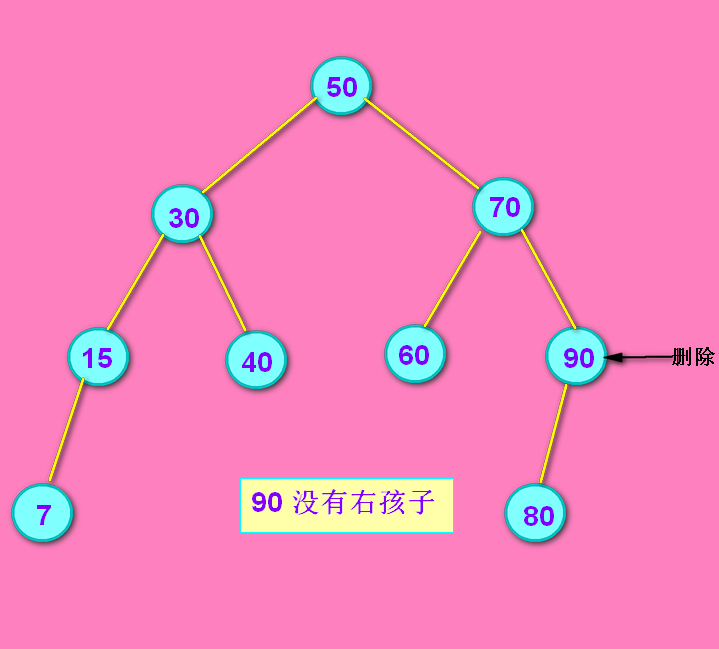
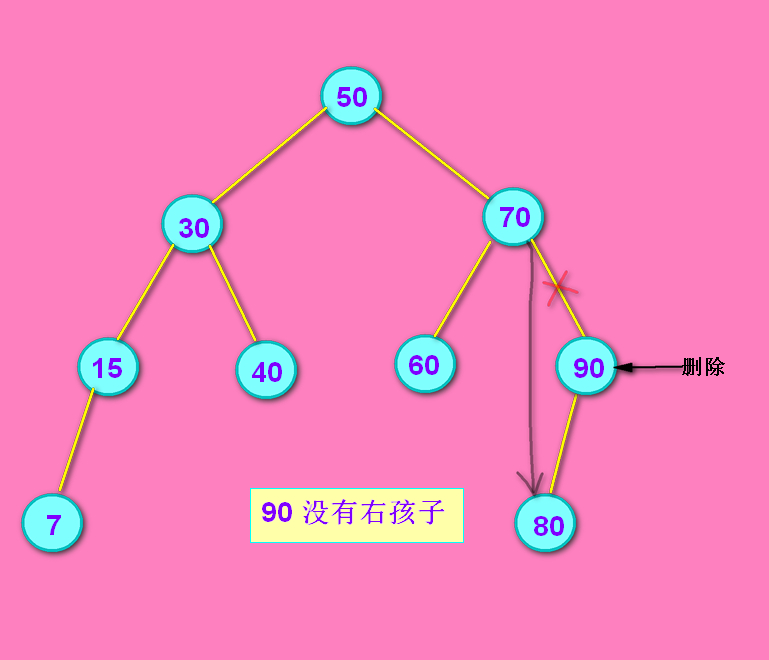
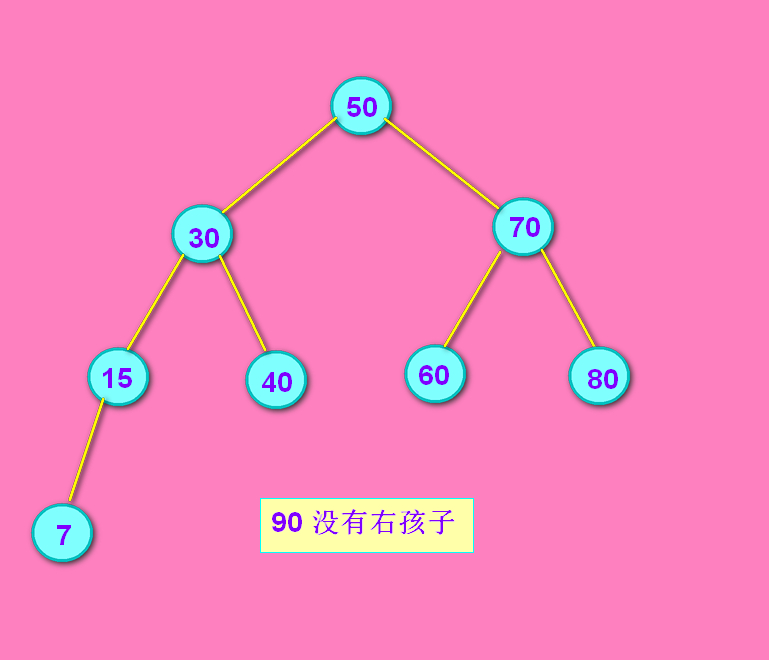
情况2： 90结点没有右孩子
没有右孩子的话，把 70结点的right 连上 90结点的left。
->
->
情况3： 90结点既有左孩子又有右孩子
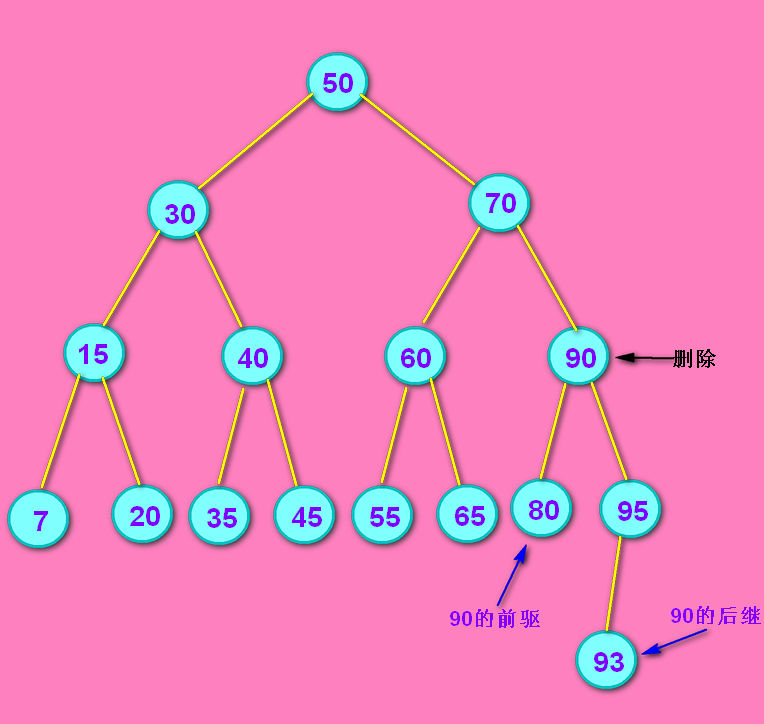
如果要删除的 90 结点情况如下，那么需要在删除前找到 90 结点的 前驱结点 或者 后继结点。如下面的第一张图。
问：找 前驱结点 / 后继结点 干嘛呢？ 答：90的前驱和后继结点是最接近90的两个结点。用他们俩替换掉90，就相当于删掉了90。如下面的第二张图。
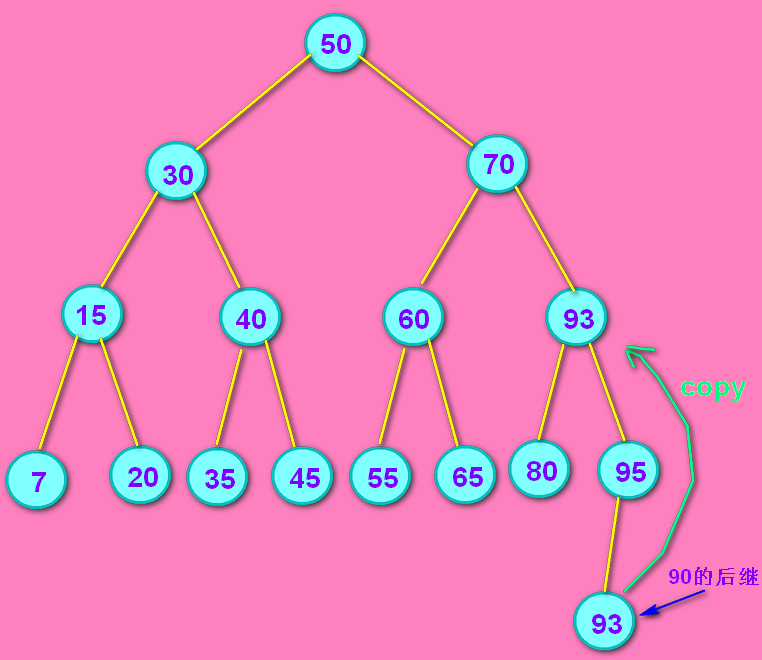
问：第二张图我看完了，你选用90的后继结点93替换了90，之后树中不就有两个93了吗？ 答：删掉原来的93就好了
问：原来的93怎么删？ 答：去新的93的右子树里找原来的93，并且删除。咱们现在介绍的是情况3(被删除的结点有左右孩子)，而且93是后继结点，肯定不会有左孩子，所以删除原来的93的问题，就回到了情况1。
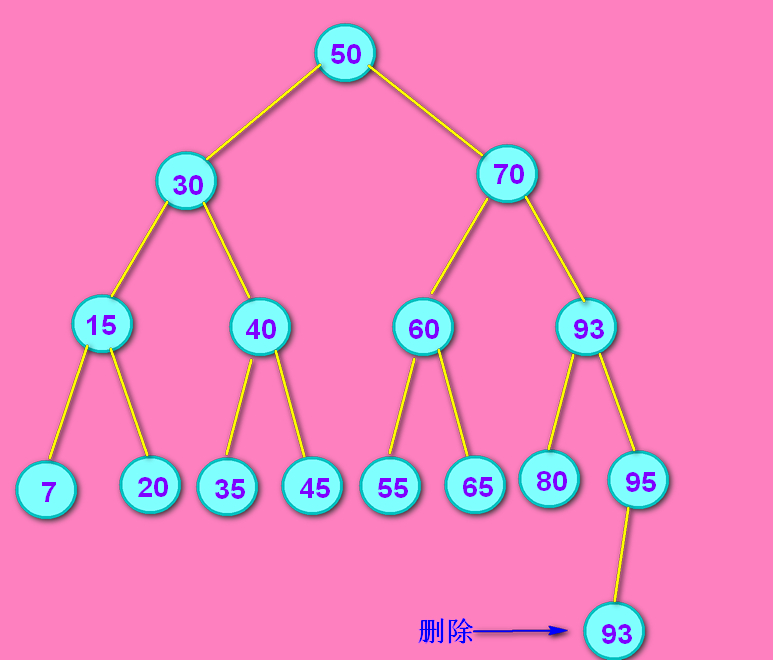
一句概括就是：在新93结点的右子树中删除原93。（见下面第3张图）
问：你图中演示的是后继结点93来替换90，那前驱结点呢？ 答：刚才说了后继结点肯定没有左孩子，而前驱结点肯定没有右孩子。用前驱80结点来替换90之后，再去删除原来的80，而这个80肯定没有右孩子，所以就回到了情况2。
一句话概括就是：如果用前驱80替换90，再删除原来的80，就回到了情况2；如果用后继93替换90，再删除原来的93，就回到了情况1。
看起来选前驱和选后继没什么两样，但是，如果90结点的右子树深，最好用后继来替换；如果90结点的左子树深，最好用前驱来替换。
->
->
问：前驱和后继怎么求呢？ 答： 首先要会求树中的最大、最小结点。从根开始向左遍历，到头了，那么这个最左边的叶子节点就是最小值。同理，一直向右遍历就是最大值。
问：那么最大最小值跟前驱后继什么关系呢？ 答：咱们以情况3的第一张图片为例。找50的前驱怎么找呢，就是50结点的左子树中的最大值。后继结点呢，就是50结点的右子树中的最小值。
问：还是不懂，给我看看代码？
答：
private Node minNode(Node node) {
if (node == null) {
return null;
} else if (node.left == null) {
return node;
} else {
return minNode(node.left);
}
}
--------------------------------------------------------
Node successor = minNode(node.right);//找node的后继结点successor
如何删除一个结点已经讲完了。
下面看看删除一个结点后都会遇到什么不平衡的情况。
假设删除前的树如下图所示，想要删除 90 结点：
删除值为90的结点后，高度差为2，不满足AVL定义。
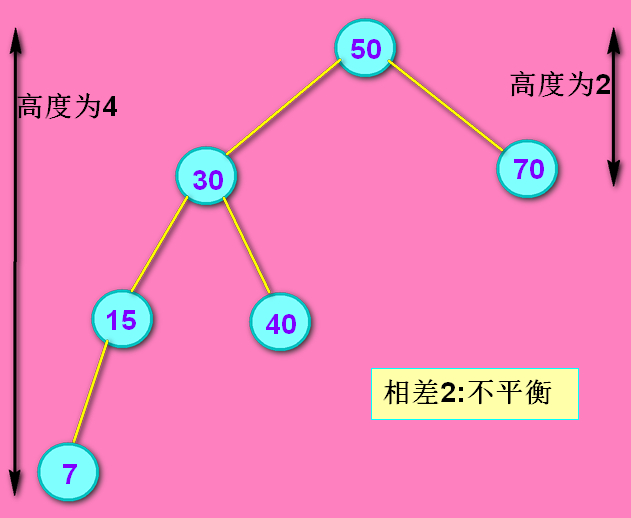
因为是删除了50 (k1) 右子树中的结点后导致的不平衡，所以肯定是左子树太深导致了不平衡。
第一个字母‘L’已经确定，所以是 LL 和 LR 结构之一。
需要判断 k2 的左右两子树，左边深，那就是LL；右边深，那就是LR。
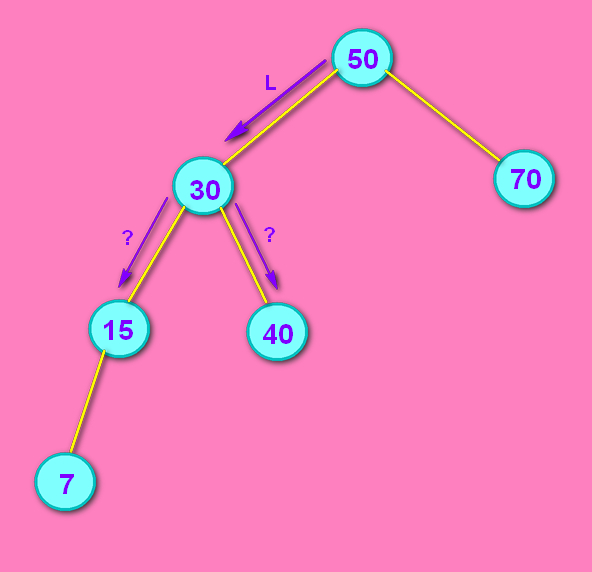---确定LL结构--->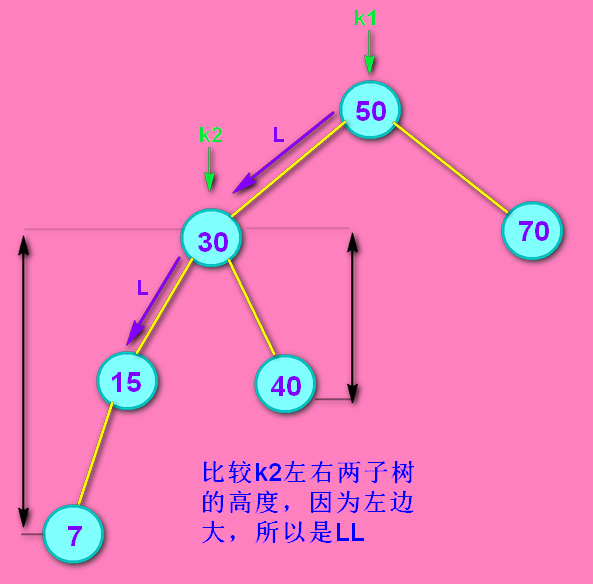
如果k2的左右两子树高度相等...那就LL/LR随意了...主要目的就是处理掉高的那部分。
AVL树完整代码
public class AVLTree<Key extends Comparable<? super Key>, Value> {
private class Node {
Key key;//键，相当于词典里的单词
Value value;//值，相当于词典里的单词解释
int height;//结点的高度
Node left;
Node right;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
int height = 1;
}
}
private Node root;
public AVLTree() {
root = null;
}
private int height(Node node) {
if (node != null) {
return node.height;
}
return 0;
}
public int height() {
return height(root);
}
private int max(int a, int b) {
return a > b ? a : b;
}
private void replaceNode(Node src, Node tar) {
tar.key = src.key;
tar.value = src.value;
}
private void preOrder(Node node) {
if (node != null) {
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
public void preOrder() {
preOrder(root);
}
private void inOrder(Node node) {
if (node != null) {
inOrder(node.left);
System.out.println(node.key);
inOrder(node.right);
}
}
public void inOrder() {
inOrder(root);
}
public void postOrder(Node node) {
if (node != null) {
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
public void postOrder() {
postOrder(root);
}
private Node search(Node node, Key key) {
if (node == null) {
return null;
} else if (key.compareTo(node.key) == 0) {
return node;
} else if (key.compareTo(node.key) < 0) {
return search(node.left, key);
} else {//key.compareTo(node.key) > 0
return search(node.right, key);
}
}
public Node search(Key key) {
return search(root, key);
}
private Node minNode(Node node) {
if (node == null) {
return null;
} else if (node.left == null) {
return node;
} else {
return minNode(node.left);
}
}
public Node minNode() {
return minNode(root);
}
private Node maxNode(Node node) {
if (node == null) {
return null;
} else if (node.right == null) {
return node;
} else {
return maxNode(node.right);
}
}
public Node maxNode() {
return maxNode(root);
}
// 对如下的LL情况
//
// k1 k2
// / \ / \
// k2 z LL单转 x k1
// / \ ----\ / / \
// x y ----/ o y z
// // / k1右旋
// o
//
// 或
//
// k1 k2
// / \ / \
// k2 z LL单转 x k1
// / \ ----\ \ / \
// x y ----/ o y z
// \ k1右旋
// o
//
private Node leftLeftRotation(Node k1) {
Node k2 = k1.left; //k2是k1的左子树
k1.left = k2.right;//k2的右子树 变为 k1 的左子树
k2.right = k1; //k1变为k2的右子树
k1.height = max(height(k1.left), height(k1.right)) + 1;//计算k1的高度
k2.height = max(height(k2.left), k1.height) + 1;//计算k2的高度
return k2;//返回新的根k2
}
// 对如下的RR情况
//
// k1 k2
// / \ / \
// x k2 RR单转 k1 k3
// / \ ----\ / \ \
// y k3 ----/ x y z
// \ k1左旋
// z
//
// 或
//
// k1 k2
// / \ / \
// x k2 RR单转 k1 k3
// / \ ----\ / \ /
// y k3 ----/ x y z
// / k1左旋
// z
//
public Node rightRightRotation(Node k1) {
Node k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max(height(k1.left), height(k1.right)) + 1;
k2.height = max(k1.height, height(k2.right)) + 1;
return k2;
}
// 对如下的LR情况
// k1 k1 k3
// / \ / \ / \
// k2 z RR单转 k3 z LL单转 k2 k1
// / \ -----\ / \ -----\ / \ / \
// w k3 -----/ k2 y -----/ w x y z
// / \ k2左旋 / \ k1右旋
// x y w x
//
public Node leftRightRotation(Node k1) {
k1.left = rightRightRotation(k1.left);
return leftLeftRotation(k1);
}
// 对如下的RL情况
// k1 k1 k3
// / \ LL单转 / \ RR单旋 / \
// w k2 -----\ w k3 -----\ k1 k2
// / \ -----/ / \ -----/ / \ / \
// k3 z k2右旋 x k2 k1左旋 w x y z
// / \ / \
// x y y z
//
public Node rightLeftRotation(Node k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
//插入
private Node insert(Node node, Key key, Value value) {
if (node == null) return new Node(key, value);
if (key.compareTo(node.key) == 0) {//如果key相同则更新该节点
node.value = value;
} else if (key.compareTo(node.key) < 0) {//如果key比当前根小，则去左子树找。即一步Left
node.left = insert(node.left, key, value);
if (height(node.left) - height(node.right) == 2) {//插在左边所以肯定是左-右，高度差2表示已经不平衡
if (key.compareTo(node.left.key) < 0) {// 又一步Left，所以是LeftLeft
node = leftLeftRotation(node);
} else { //一步Right，所以是LeftRight
node = leftRightRotation(node);
}
}
} else { // node.key < key,那么去右子树找.即一步Right
node.right = insert(node.right, key, value);
if (height(node.right) - height(node.left) == 2) {//插在右边所以肯定是右-左，高度差2表示已经不平衡
if (key.compareTo(node.right.key) > 0) {//又一步Right,所以是RightRight
node = rightRightRotation(node);
} else {//一步Left，所以是RightLeft
node = rightLeftRotation(node);
}
}
}
node.height = max(height(node.left), height(node.right)) + 1;
return node;
}
public void insert(Key key, Value value) {
this.root = insert(this.root, key, value);
}
//删除
/**
* @param node 当前子树根节点
* @param target 要删除的结点
* @return 删除后的新的子树根
*/
public Node remove(Node node, Node target) {
if (node == null || target == null) return node;
if (target.key.compareTo(node.key) < 0) {//待删除key的比根的key小，那么继续在左子树查找
node.left = remove(node.left, target);
if (height(node.right) - height(node.left) == 2) {//如果在删除后失去平衡
if (height(node.right.left) <= height(node.right.right)) {
node = rightRightRotation(node);
} else {
node = rightLeftRotation(node);
}
}
} else if (node.key.compareTo(target.key) < 0) {//待删除key的比根的key大，那么继续在右子树查找
node.right = remove(node.right, target);
if (height(node.left) - height(node.right) == 2) {
if (height(node.left.right) <= height(node.left.left)) {
node = leftLeftRotation(node);
} else {
node = rightRightRotation(node);
}
}
} else { // node.key == target.key
if (node.left == null) { // 如果node的左子树为空，那么删除node后，新的根就是node.right
return node.right;
} else if (node.right == null) {// 如果node的右子树为空，那么删除node后，新的根就是node.left
return node.left;
} else { // 如果node既有左子树，又有右子树
if (height(node.left) > height(node.right)) {//如果左子树比右子树深
Node predecessor = maxNode(node.left);//找node的前继结点predecessor
replaceNode(predecessor, node);//predecessor替换node
node.left = remove(node.left, predecessor);//再把原来的predecessor删掉
} else {//如果右子树比左子树深(一样深的话无所谓了)
Node successor = minNode(node.right);//找node的后继结点successor
replaceNode(successor, node);//successor替换node
node.right = remove(node.right, successor);//再把原来的successor删掉
}
}
}
return node;
}
public void remove(Key key) {
Node z;
if ((z = search(root, key)) != null)
root = remove(root, z);
}
private void destroy(Node node) {
if (node == null)
return;
if (node.left != null)
destroy(node.left);
if (node.right != null)
destroy(node.right);
node = null;
}
public void destroy() {
destroy(root);
System.out.println("销毁完毕");
}
private void print(Node tree, Key key, String pos) {
if (tree != null) {
if (pos.equals("")) // tree是根节点
System.out.printf("%2d is root\n", tree.key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, pos);
print(tree.left, tree.key, "left");
print(tree.right, tree.key, "right");
}
}
public void print() {
if (root != null) print(root, root.key, "");
}
//***************************************************************
private static int arr[] = {3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9};
public static void main(String[] args) {
int i;
AVLTree<Integer, Integer> tree = new AVLTree<>();
System.out.printf("*******依次添加: ");
for (i = 0; i < arr.length; i++) {
System.out.printf("%d ", arr[i]);
tree.insert(arr[i], arr[i]);
}
System.out.println();
System.out.print("*******前序遍历: ");
tree.preOrder();
System.out.println();
System.out.print("*******中序遍历: ");
tree.inOrder();
System.out.println();
System.out.print("*******后序遍历: ");
tree.postOrder();
System.out.println();
System.out.println("*******高度:" + tree.height());
System.out.println("*******最小值:" + tree.minNode().key);
System.out.println("*******最大值:" + tree.maxNode().key);
System.out.println("*******树的详细信息:");
tree.print();
System.out.println();
i = 8;
System.out.printf("*******删除根节点: %d", i);
tree.remove(i);
System.out.println();
System.out.println("*******高度:" + tree.height());
System.out.println("*******中序遍历: ");
tree.inOrder();
System.out.println();
System.out.println("*******树的详细信息:");
tree.print();
System.out.println();
// 销毁二叉树
tree.destroy();
}
}
学如不及，犹恐失之
