斐波那契数列

今天上课讲了一些数论，本蒟蒻并没有听懂，于是只好写一个斐波那契数的总结来弥补一下啦qwq。

首先来了解一下斐波纳契数列的定义

设斐波纳契数列的第i项是F(i)，斐波那契数列的递推公式可以写成F(i)=F(i-1)+F(i-2) (i>2)，F(1)=1，F(2)=1。
通项公式的话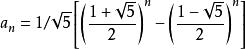，把ai改成Fi就是了，copy图片时没有对应的，望谅解。

斐波那契数列的一些性质

1. lim(i->oo) F(i)/F(i+1)=(sqrt(5)-1)/2，也就是斐波那契数列越靠后相邻两项的比值越接近黄金分割比，证明如下：
   F(i)=F(i-1)+F(i-2)
   两边同时除以F(i-1)得：
   F(i)/F(i-1)=1+F(i-2)/F(i-1)
   设lim(i->oo) F(i)/F(i+1)=x
   则：lim(i->oo) F(i-1)/F(i)=F(i-2)/F(i-1)=x
   代入上面那个式子，1/x=1+x
   解得：x=(sqrt(5)-1)/2
   到此原命题得证
2. F(n-1)*F(n+1)-F(n)^2=(-1)n，证明此处省略，套递推公式就行了。
3. 集合{1,2,3,4,……,n}没有相邻两个正整数的子集个数为F(n+2)，证明略。
4. F(1)+F(3)+F(5)+……+F(2n-1)=F(2n)-F(2)+F(1)
5. F(2)+F(4)+F(6)+……+F(2n)=F(2n+1)-F(1)
6. ∑(i=:1 to n) F(i)^2=F(n)*F(n+1)
7. F(2n)/F(n)=F(n-1)+F(n+1)
8. gcd(F(a),F(b))=F(gcd(a,b))，证明可参考这篇文章
9. gcd(2^p1-1,2p2-1,……,2^pk-1)=2gcd(p1,p2,……,pk)-1

参考文献及推荐资料：
https://baike.baidu.com/item/斐波那契数列/99145?fr=aladdin#4_4
（没错，就是百度，百度上的还挺全面的，有很多扩展，值得一看）
https://blog.csdn.net/qq_37891604/article/details/81604939
https://blog.csdn.net/alan_cty/article/details/73928751