问题:
1维,1米长的路面,每次下一滴雨,每滴雨落到地面上长度是0.01米,落点假设均匀分布,求问下了多少滴雨之后路面会全部湿透,求期望?
分析:
把一米长的路面分成100个格子,每个格子都落了雨滴了那么路面就湿透了。随机性在于每次哪个格子落雨是不确定的。 分析到这,了解优惠券收集问题的人应该知道这其实可以归约到该问题的。那么优惠券收集问题是怎样的呢?
优惠券收集问题:
有个餐馆,每天随机发印有12生肖中的一种生肖的优惠券,小明每天都去该餐馆。问小明期望需要几天能收集到所有12生肖图案的优惠券。
这个问题如果直接去求,从至少需要12天开始,计算每种可能的概率进而计算期望会很麻烦。 我们借助概率性质:
随机变量的和的期望等于这些随机变量期望之和
对于这个问题,我们需要把要求的期望分解为若个个随机变量的和。(E(X1+X2)=E(X1)+E(X2), 当 X1, X2相互独立时)
设随机变量S表示收集到所有生肖优惠券所需的最少天数, 我们用Xi表示收集到(i-1)种优惠券后,还需要多少天才能收集到第i种优惠券。
-
X1表示收集到第一种优惠券所需天数,显然X1=1
-
我们来算X2,收集到第一种后,除了第一种的优惠券,其他任何一种都可以算第二种了,从而,他每天出现的 概率为11/12,进而期望天数为12/11 【1】(每天可以看出一个独立的贝努利实验)
-
类似X3的期望为12/10, E(Xi)=12/(13-i) (i取值从1到12)
我们有S=X1+X2+...X12,
E(S)=E(X1)+E(X2)+...+E(X12) = 12(1+1/2+1/3+..1/12)。
括号里面的那个为调和级数,近似地1+1/2+....1/n =log(n) (可以从积分角度证明)
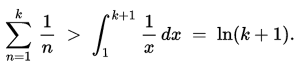
现在我们回到原题,100个格子可以看出100种优惠券,从而期望雨滴数为100(1+1/2+....1/100).
【1】根据伯努利分布计算天数期望的推导过程如下图:

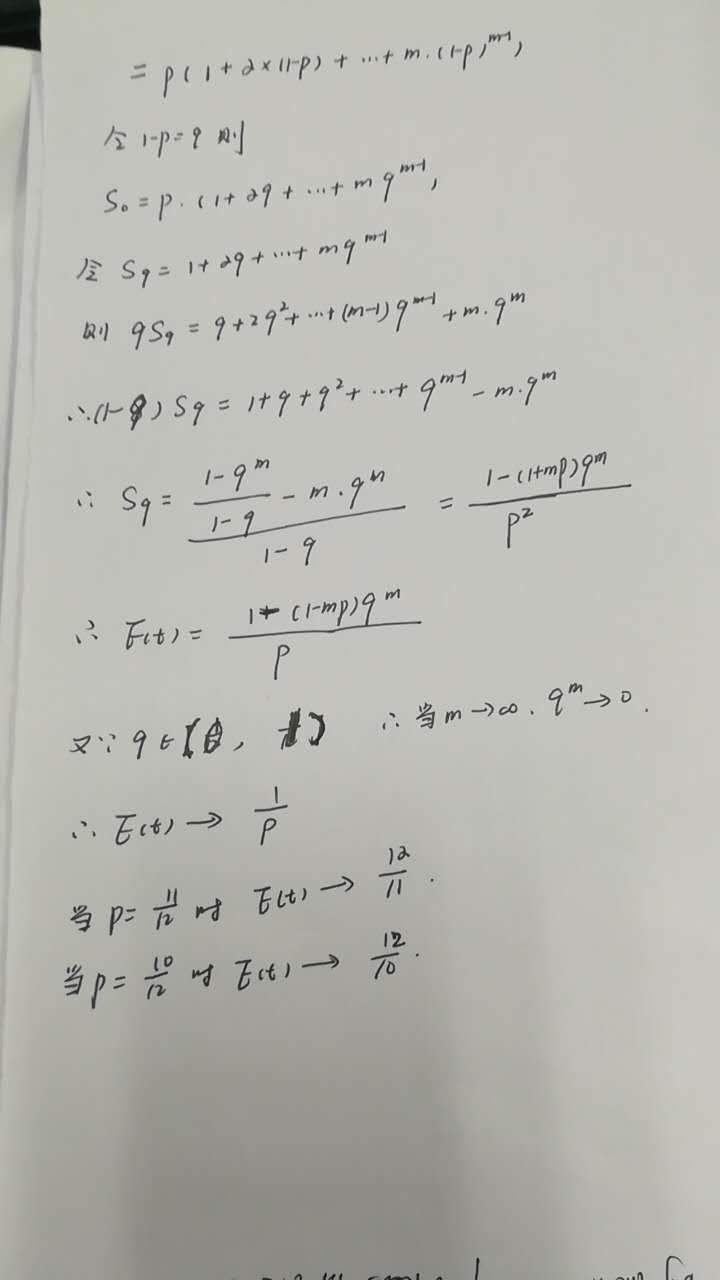
变种
这个问题特别经典,有些问题可能比这题看起来更不容易归约,作为练习,大家可以考虑下面的问题:
假设给定长度N的数组,我们需要对数组里的元素做随机打乱,采用如下算法, 请给出该算法复杂度:
1) 从第一个元素开始,我们随机产生一个1到N之间的下标,也用这个下标的元素跟第一元素交换
2) 处理第i个位置时,我们仍然是先随机产生一个1到N之间的下标,如果产生的下标在[1,i-1]中,我们丢弃这个下标,重现取个新的,直到满足要求
3) 处理完N个位置后,原数组被随机打乱了



