SPH算法(求最小代价树)
一、sph算法简介
1.最小代价树算法
SPH算法也叫做MPH( minimum path heuristic)算法, 用于构造时延约束最算法小代价组播树. 该算法中每 个目的结点通过与当前组播树有最小代价的路径加入组播树,直到所有的目的节点全的进入树。
最小代价树算法中最经典的算法有 3 个: KMB 算法、ADH 算法、 MPH 算法.
- KMB 算法是由 Kou 等人提出的求解 Steiner 组播树算法, 其复杂度为 O(mn2);
- ADH ( average distance heuristic)算法复杂度为 O( n3);
- MPH 算法复杂度为 O( mn2).
2.MPH算法过程
到目前为 止,从降低组播生成树的代价方面考虑,MPH 仍是 一个非常优秀 的求解 Steiner 树问题 的启发式 算法. MPH 算法基本思想如下:
-
- 初始化组播树 T,开始时只包括源结点 s;
-
- 从余下的目的结点中选取到树 T 具有最小 代价路径的目的结点,将该结点及其最小代价路径 加入树 T ;
-
- 重复 2) ,直到所有目的结点加入组播树 T
3.SPH算法过程
具体包括如下几个 步骤:
- 1)运用 Dijkstra算法,以点集S(初值为源点first)计算到所有结点的最小代价路径 ;
- 2)选出目的节点中间的代价最小的minNodes;
- 3)将到点minNodes的路径上的全部节点压进点集S;
- 4)重复1)、2)、3)直到所有的目标点集进入点集S;
其中Dijkstra算法是一个常用的解单源最短路径的常用算法。其基本思想是,设置一个顶点集合H,并不断贪心的选择来扩充这个集合。此算法网上描述很多,不进行赘述。
本次,完成Dijkstra后同时记录下最短路径的值及最短路径经过的节点,数据结构也只是用了比较low的表去实现。
第二步中间选取最小的minNodes时,下一步的优化方向是采用最小优先级对列的数据结构,及堆算法pop_heap,push_back,pop_back等等。
二、代码实现
核心代码:
for (;;)
{
if (t > 0)
{
t = T;
mind = 99999999;
//所有点到目标点的距离
for (int i = 1; i <= DD; i++)
{
if (s[i] == 1)
{
Dijkstra(i);
//利用新的dist的数据对fdis的数据进行更新
for (int j = 1; j <= DD; j++)
{
if (dist[j] < fdis[j] && dist[j] != 0 && s[j] != 1)
{
fdis[j] = dist[j];
for (int k = 0; k <= DD; k++)
{
fload[j][k] = load[j][k];
if (fload[j][k] == 0)
break;
}
}
}
}
}
fdis[first] = 0;
//找出最小的点(目标点中)
for (int i = 1; i <= DD; i++)
{
for (int j = 0; j < T; j++)
{
if (mind > fdis[i] && i == goal[j] && goal2[i] != 1)//这点距离小,在目标点中间,且未进入点集s
{
mind = fdis[i];
minv = i;
}
}
}
//找出的点加入点集s
goal2[minv] = 1;
for (int i = 0; i <= DD; i++)
{
if (fload[minv][i] > 0)
s[fload[minv][i]] = 1;
else
break;
}
for (int i = 1; i <= DD; i++)
{
if (1 == goal2[i])
t--;
}
}
else
break;
}
贴几个跑完的数据。
- 数据1:
first:2
目标点1、2、3、4、5、6、7、8、9、10
点集图:
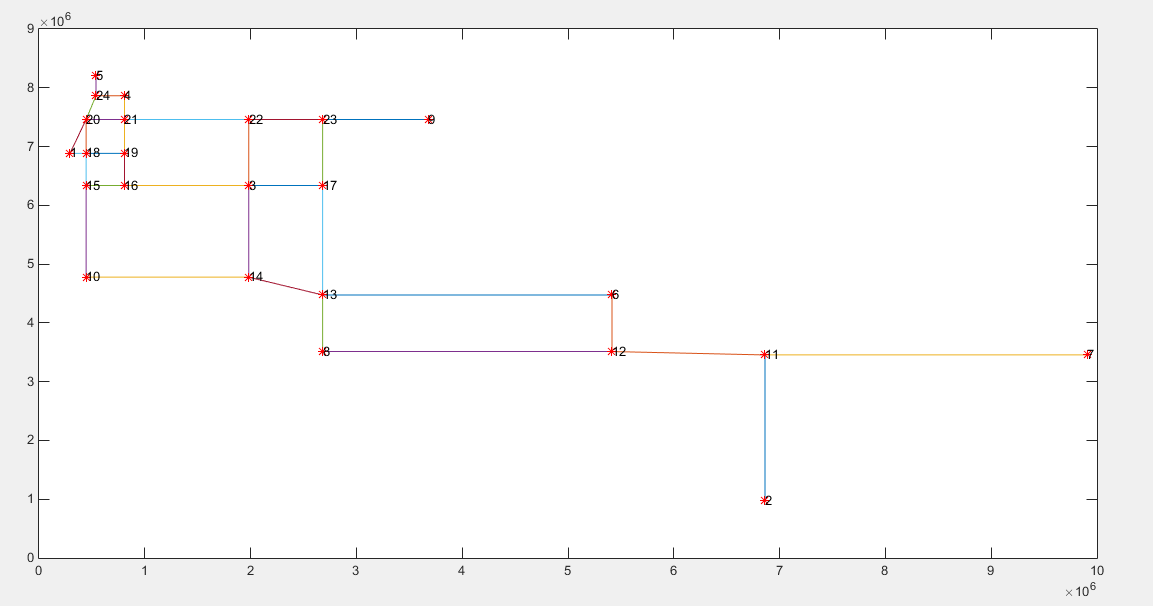
路径图:(别吐槽。。。matlab用的烂,有空补不是手绘的。。。)
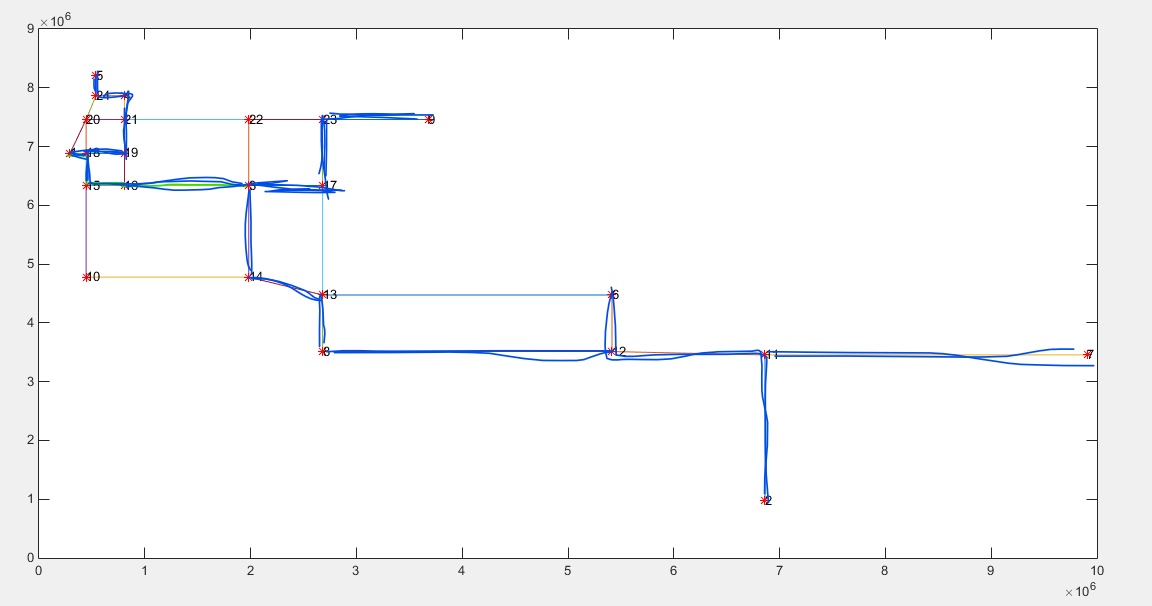
程序结果截图:
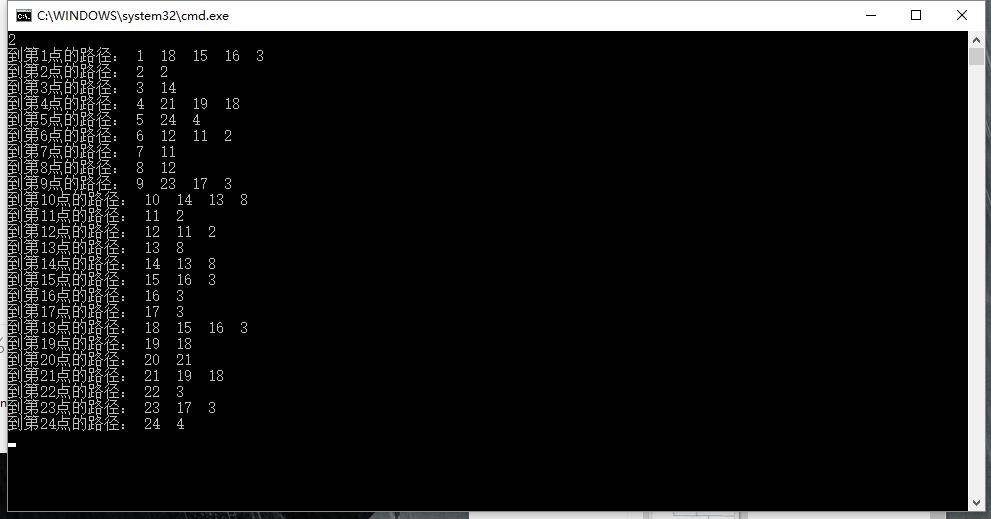
- 数据2:
first:1
目标点1、2、3、4、5、6、7、8、9、10
点集图:
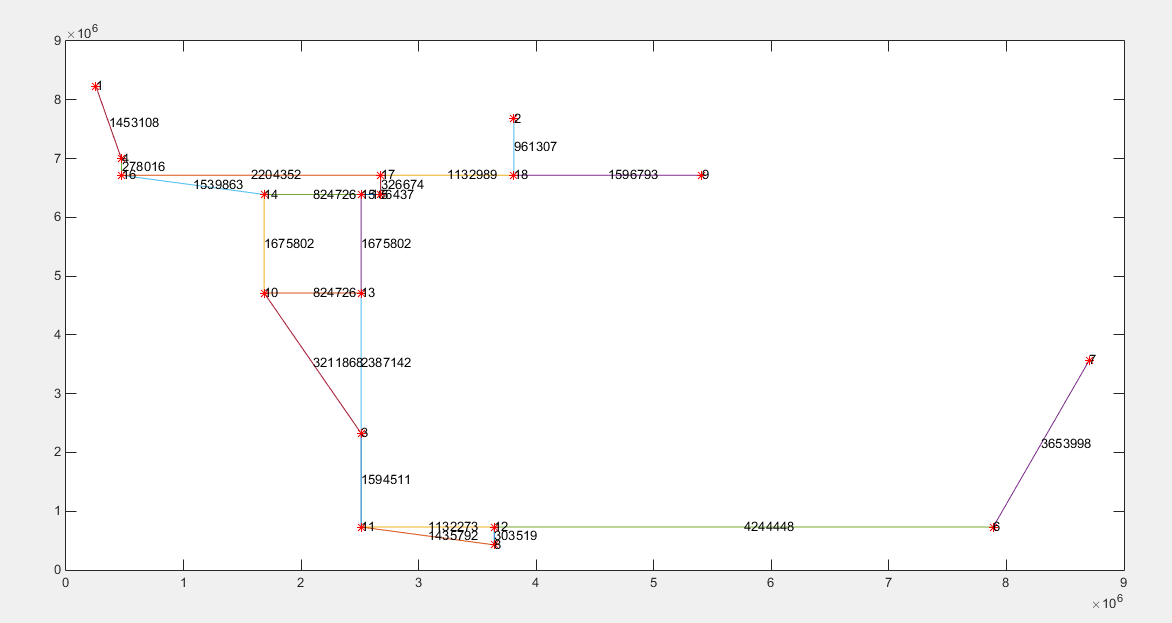
路径图:

程序结果截图:
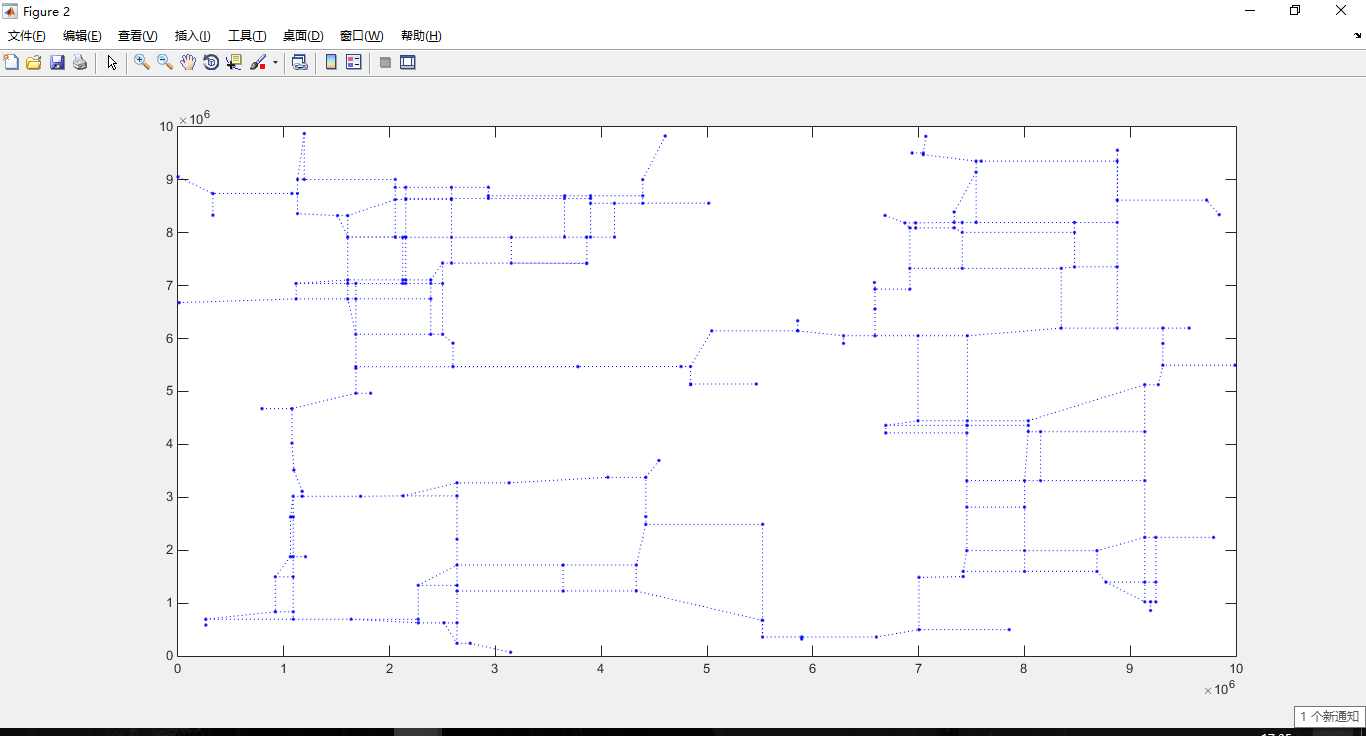
-数据3:
点集图:
路径图:
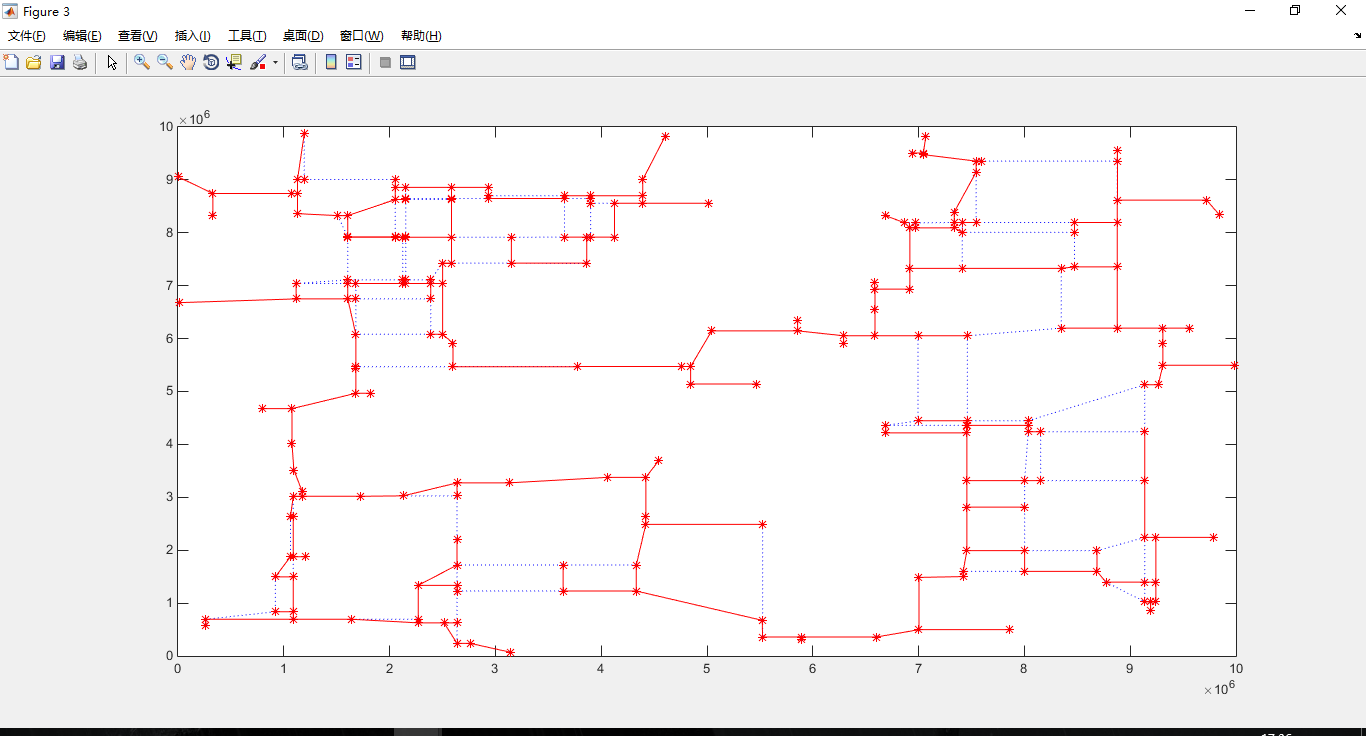
emmmmm........就是这样,学习中大佬们指教。



