二叉树的应用:二叉排序树的删除
二叉排序树有两种删除结点的思路:
方法一
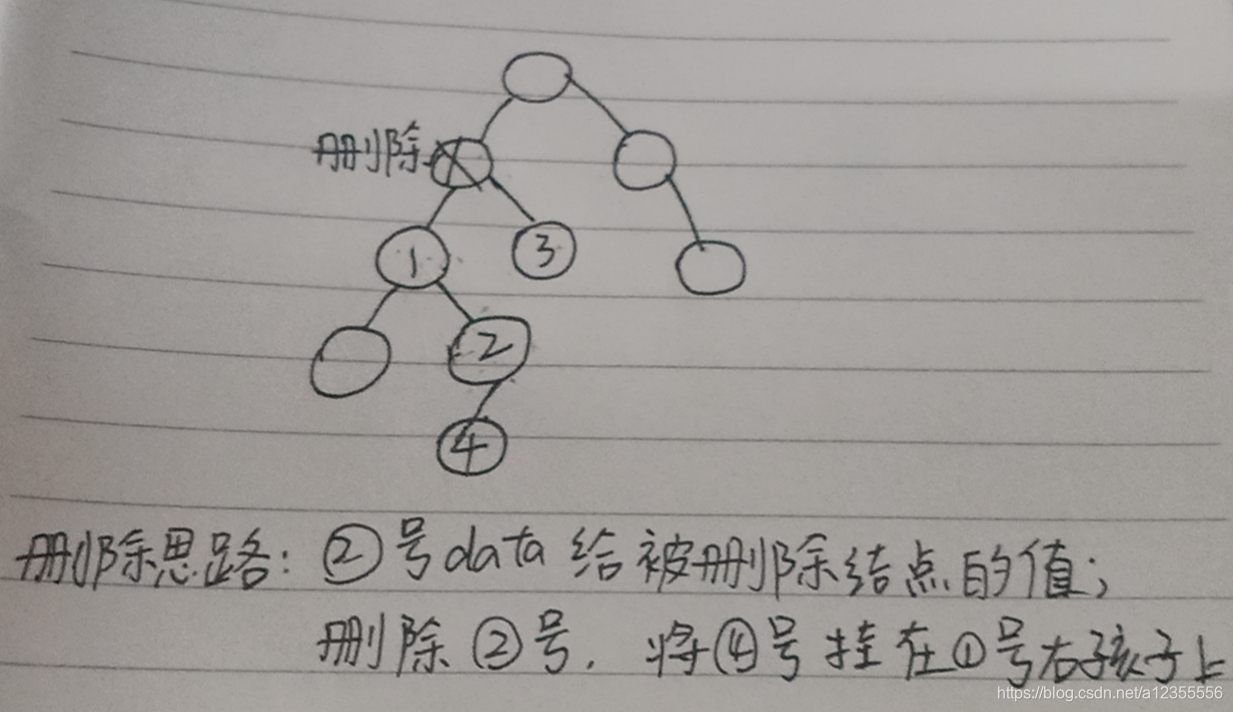
代码:
public void del1(int x) {
BiTreeNode p = root;
//设置父结点,下面会用到
BiTreeNode parent = null;
//找到要删除的结点,找不到就结束删除
while (p != null && p.data != x) {
parent = p;
if (x > p.data) {
p = p.rchild;
} else {
p = p.lchild;
}
}
if (p == null) {
System.out.println("error");
return;
} else if (p.data == x) {
//第一种情况,要删除的结点度数为2
if (p.lchild != null && p.rchild != null) {
BiTreeNode temp = p;
//parent2为要删除结点的左侧最大值结点的父结点
//temp为要删除结点的左侧最大值结点
BiTreeNode parent2 = temp;
temp = p.lchild;
//更换要删除结点的数据
p.data = getMax2(temp).data;
while (temp.rchild != null) {
parent2 = temp;
temp = temp.rchild;
}
if (temp.lchild == null) {
//需要注意待删节点的左节点开始寻找的最大值结点是否为本身
if (parent2.lchild == temp) {
parent2.lchild = null;
} else {
parent2.rchild = null;
}
} else {
if (parent2.lchild == temp) {
parent2.lchild = temp.lchild;
} else {
parent2.rchild = temp.rchild;
}
}
} else {
//第二种情况,要删除的结点度数为1
BiTreeNode child;
if (p.lchild != null) {
child = p.lchild;
} else if (p.rchild != null) {
child = p.rchild;
} else {
child = null;
}
if (parent.lchild == p) {
parent.lchild = child;
} else if (parent.rchild == p) {
parent.rchild = child;
}else{
root=child;
}
}
}
}
public BiTreeNode del2(BiTreeNode p, int x) {
if (p == null) {
System.out.println("empty error");
return p;
}
if (x < p.data) {
p.lchild = del2(p.lchild, x);
} else if (x > p.data) {
p.rchild = del2(p.rchild, x);
} else {
if (p.lchild != null && p.rchild != null) {
BiTreeNode temp = p.lchild;
p.data = getMax2(temp).data;
p.lchild = del2(p.lchild, p.data);
} else if (p.lchild == null) {
p = p.rchild;
} else if (p.rchild == null) {
p = p.lchild;
}
}
root=p;
return p;
}
提示:
del1是非递归版,按照思路进行
del2是递归版
方法二
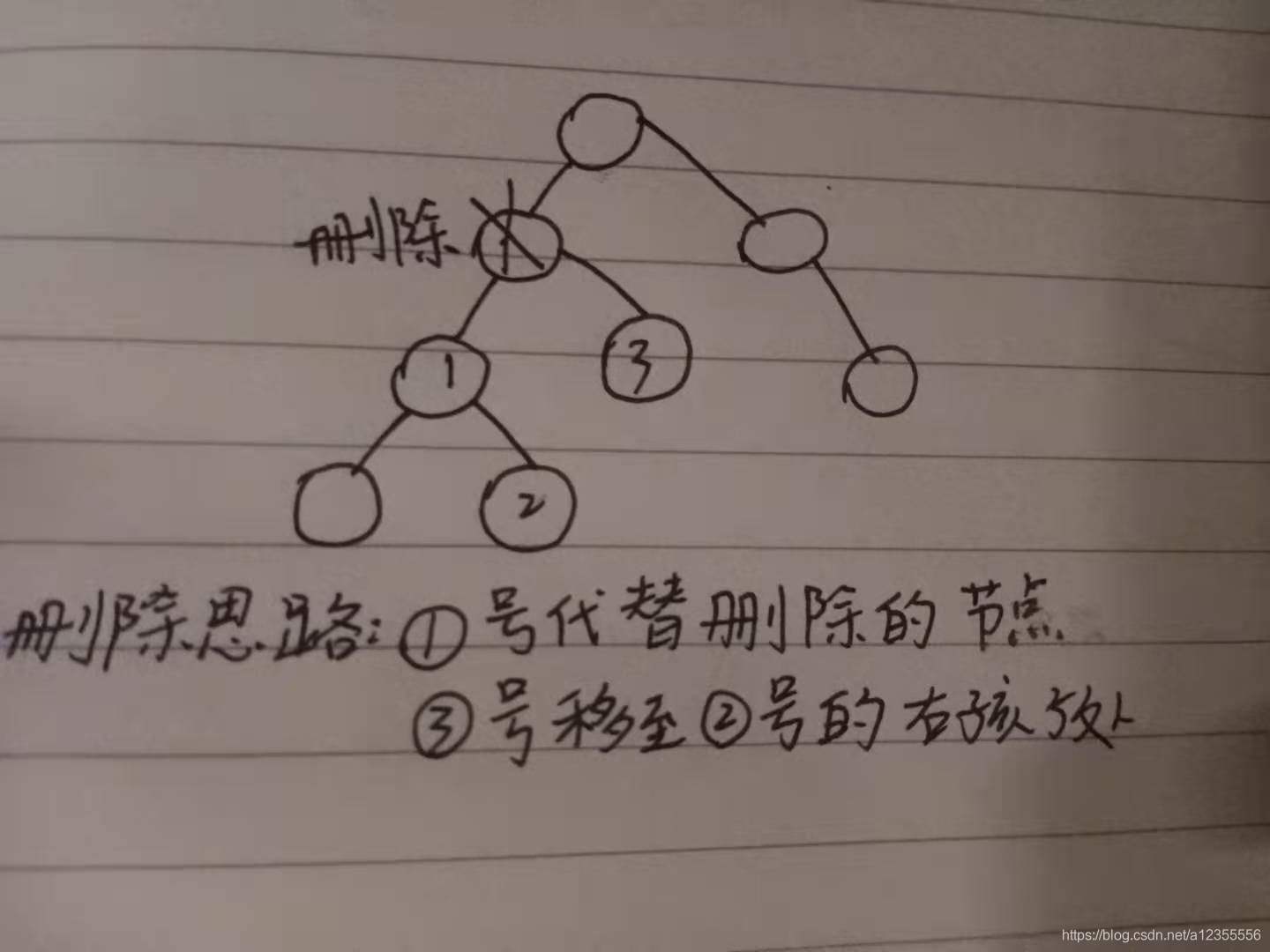
代码:
public void del3(int x) {
BiTreeNode p = root;
BiTreeNode parent = p;
while (p != null && p.data != x) {
parent = p;
if (x < p.data) {
p = p.lchild;
} else if (x > p.data) {
p = p.rchild;
}
}
if (p == null) {
return;
} else {
if (p.rchild != null) {
BiTreeNode temp = p.lchild;
if (parent.lchild == p) {
parent.lchild = temp;
} else if (parent != null && parent.rchild == p) {
parent.rchild = temp;
} else {
if (p.lchild != null) {
root = p.lchild;
} else if (p.rchild != null) {
root = p.rchild;
}
}
getMax2(temp).rchild = p.rchild;
} else {
BiTreeNode child = null;
if (p.lchild != null) {
child = p.lchild;
} else if (p.rchild != null) {
child = p.rchild;
}
if (parent.lchild == p) {
parent.lchild = child;
} else if (parent.rchild == p) {
parent.rchild = child;
}else{
root=child;
}
}
}
}
public BiTreeNode del4(BiTreeNode p, int x) {
if (p == null) {
return p;
}
if (x < p.data) {
p.lchild = del4(p.lchild, x);
} else if (x > p.data) {
p.rchild = del4(p.rchild, x);
} else {
if (p.lchild != null && p.rchild != null) {
BiTreeNode temp = getMax2(p.lchild);
temp.rchild = p.rchild;
p.rchild = null;
p = p.lchild;
} else if (p.lchild == null) {
p = p.rchild;
} else if (p.rchild == null) {
p = p.lchild;
}
}
root=p;
return p;
}
注意:
del3为非递归
del4为递归
此方法由于可能改变root位置(即在删除根节点的时候),需要格外注意root需要实际意义上的改变
(即直接对root改变)
上一种方法只改变了root值,实际并未改变结点位置,所以不需注意实际意义的改变。
(p=root,p.data=1 则root.data=1; p=p.lchild,但root仍然不变,变的是p,要想使root也变,
需要使用返回值返回,将结点挂在父节点上(如果删除的是root,没有父节点则无法使root改变 )或者在函数最后使root=p)
补充:
上方代码用到的获取树最大值 代码如下:
public BiTreeNode getMax2(BiTreeNode p) {
if (p == null) {
System.out.println("error p结点data为空");
return null;
}
if (p.rchild == null) {
return p;
}
return getMax2(p.rchild);
}


