Tourist Attractions 【三元环】

 

 

本人水平有限，题解不到为处，请多多谅解

 

本蒟蒻谢谢大家观看

 

 

题目：

题目描述

在美丽的比特镇一共有n个景区，编号依次为1到n它们之间通过若干条双向道路连接。 Byteasar 慕名来到了比特镇旅游，不过由于昂贵的门票费，他只能负担起 4 个景区的门票费。他可 以在任意景区开始游览，然后结束在任意景区。 Byteasar 的旅游习惯比较特殊，一旦他路过了一个景区，他就一定会进去参观，并且他永远不会参 观同一个景区两次。所以他想知道，有多少种可行的旅游路线，使得他可以恰好参观 4 个景区呢？即 有多少条简单路径恰好经过了 4 个点。

输入格式

第一行包含两个整数n,表示景区的总数。 第 2 至第 n +1 行，每行一个长度为 n 的 01 字符串，第 i+1 行第 j 个字符为 0 表示 i 和 j 之间 没有道路，为 1 表示有一条道路。 输入数据保证 (i,j) 的连接情况等于 (j,i) 的连接情况，且 (i,i) 恒为 0。

输出格式

输出一行一个整数，即可行的路线总数。

样例输入
4 
0101
1010 
0101 
1010
样例输出
8

本题大意：

找出一个三元环，因为三元环一定不能满足题目意思。

本题只需要有一条路径能经过4个不同的点即可(可以为环)

如果不是三元环，我们就用排列组合来求出不是三元环的。

我们可以先全部当成可行方案，最后把三元环的数给减掉即可

三元环用bitset优化

因为统计的ans会爆int，因为我们用排列组合方式求，所以要开long long

具体bitset应用请点：click_here

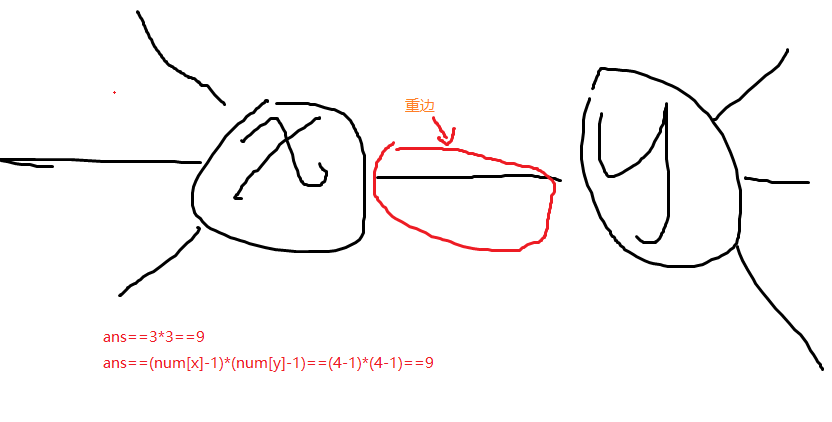
 ans+=(num[i]-1)*(num[y]-1); 

看上面一段代码，为什么统计答案要这样写呢？

看下面一幅图：

 

 

也就是类似于小学数学的统计方案数

code:

#include<bits/stdc++.h>
#pragma GCC optimize(3)
const int N=1510;
using namespace std;
char a[N][N];
bitset<N>sum[N],p;
int num[N],tot,n;
long long ans=0;
int ver[N*N],head[N*N],nxt[N*N];
void inint(){
    freopen("tour.in","r",stdin);
    freopen("tour.out","w",stdout);
}
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*f;
}
inline void write(int x)
{
    if(x<0)x=-x,putchar('-');
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
void add(int x,int y){
    ++tot;
    ver[tot]=y;
    nxt[tot]=head[x];
    head[x]=tot;
    num[x]++;//统计度数 
}
int main()
{
    //inint();
    n=read();
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>a[i][j];
            if(a[i][j]=='1'){
                sum[i][j]=1;//有边 
                add(i,j);//建单向边 
            }
        }
    } 
    for(int i=1;i<=n;i++){
        for(int j=head[i];j;j=nxt[j]){
            int y=ver[j];
            ans+=(num[i]-1)*(num[y]-1);//减掉父亲连向儿子这一条边，避免重复运算 
            p=sum[i]&sum[y];//统计有多少个1，即三元环的个数 
            ans-=p.count();
        }
    }
    printf("%lld\n",ans);
    return 0;
}