并查集浅谈及其扁平化

 

 

本人水平有限，题解不到为处，请多多谅解

 

本蒟蒻谢谢大家观看

 

 

并查集（普及基本知识）
1：目的
并查集的目的很容易理解，通俗点就是说你的亲戚的亲戚也是你的亲戚，用来检测任意两点是否同在一个集合内。
2：实现办法
实现的办法主要判断两点的最远公共祖先是否一样（亦就是两点所在的集合的根节点），我们可以定义一个fa[i]数组表示i的父亲，一开始所有点的父亲都是他自己（因为一开始每个点所代表的集合只有该点一个点而已，所以这个集合的根节点就是该点），随后会读进来几组数据，例如A B，则代表点A和点B是亲戚。则将fa[A]赋值为B或者将fa[B]赋值为A(如果是普通并查集，是对的)。(如果是扁平化)显然是不对的，因为A和B的合并并不仅仅代表这两点，而是他们所在的集合。举个例子：你和一个女孩成了亲，那么原来她爷爷的奶奶的爷爷的奶奶的…以前和你没半毛钱关系，但是现在你爷爷的奶奶的爷爷的奶奶的…都和此人成为了亲戚，所代表的就是你和她的集合合并了。
3：合并点分别在的集合的根节点
可能听起来有些拗口，但实际上还是很容易理解的，我们可以定义一个find函数，find(x)表示点x所在的集合的根节点，那么我们只要询问点x的父亲点是否为他自己，如不是再询问x的父亲…一直找到根节点为止，那么就有这样一段代码：

code:

int find(int o)
{
    if(o==fa[o])return o;//如果点o的父亲点是他自己，那么本集合的根节点就是点o
    return find(fa[o]);//如不是，则去询问点o的父亲
}

4：扁平化处理
上述代码不难看出是一种递归的思想，如果数据过大就会造成很多无用的浪费，由于并查集只要求合并点的集合的根节点的关系，我们索性就设fa[i]直接赋值为i所在的集合的根节点（因为其他的点无用），比方说原先有这样一个集合:

 

 

 

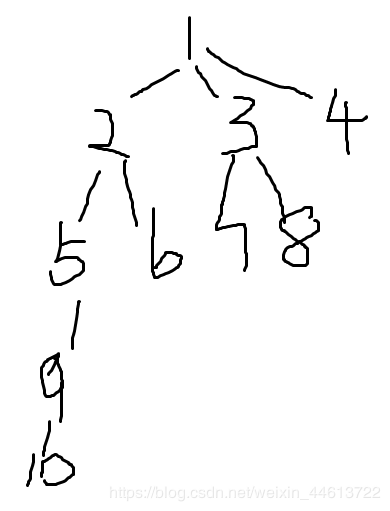
而经过这么一处理就变成了(中间画不下了，就用省略号代替):

 

 

 

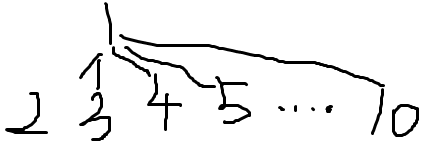
这样原来搜寻find(10)要递归5次，而扁平化处理之后只需2次。其实代码很简单写的：

code:

int find(int o)
{
    if(o==fa[o])return o;
    return fa[o]=find(fa[o]);//直接将fa[o]赋值为该集合的根节点
}