种树 反悔操作 【贪心】

 

本人水平有限，题解不到为处，请多多谅解

 

本蒟蒻谢谢大家观看

 

 

题目：传送门

 

 

具体的解析大佬博客里有

 

推荐：博客

 

我这里是来讲下如何代码实现的

 

我们用pair来实现堆优化，first代表权值，second代表权值位置

 

void del(int x){
    pre[nxt[x]]=pre[x];
    nxt[pre[x]]=nxt[x];
    flag[x]=true;
}

以上代码如何理解呢？

先看一幅图：

我们先算4个点

 

 

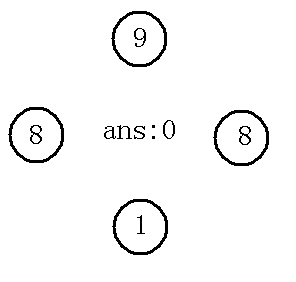
如果依照最基本的贪心策略（即取最大值）

应该是这样：

 

 

 

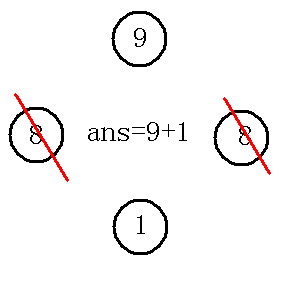
 但是我们发现这并不是最优解，ans==10，明显小于 ans==16

这时就要进行反悔操作，即赎买 ，算差值

记录我们取的当前节点的最大值与其左右两个节点之和的差值 (来方便赎买) 即反悔操作

可知：差值为7 (8+8-9=7)

 

 

 

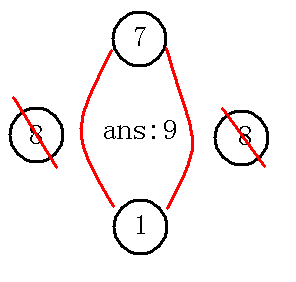
 这时我们把7放到原先9的位置上

我们发现8在我们取9的时候被打上了标记，不能取

即：

flag[x]=true;

 

对于不能取的点，我们要让其退出堆内，即：

while (flag[Q.top().second]){
        Q.pop();
    }

这时堆里的最大值为7，就取出7来更新ans

 

 

 

pre[nxt[x]]=pre[x];
    nxt[pre[x]]=nxt[x];

 

 

所以这两句话的意思是：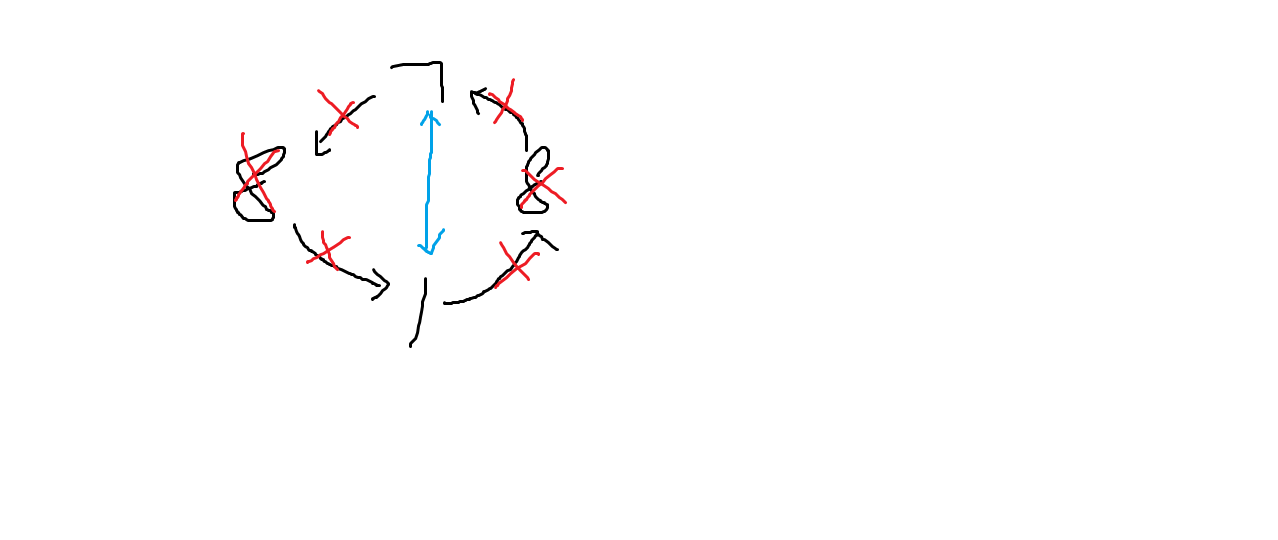

 

如果当m的两倍大于n的话，显然是无法种完m的（隔板插空），所以直接输出 Error!

 

 

code:

#include<bits/stdc++.h>
#pragma GCC optimize(3)
#define int long long
const int N=1e6+10;
using namespace std;
bool flag[N];
int n,m,ans,node[N],pre[N],nxt[N];
priority_queue<pair<int,int> > Q;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*f;
}
void del(int x){
    pre[nxt[x]]=pre[x];
    nxt[pre[x]]=nxt[x];
    flag[x]=true;
}
void greedy(){
    while (flag[Q.top().second]){
        Q.pop();
    }
    int a=Q.top().second;
    Q.pop();
    ans+=node[a];
    node[a]=node[nxt[a]]+node[pre[a]]-node[a];
    del(pre[a]);
    del(nxt[a]);
    Q.push(make_pair(node[a],a));
}
signed main()
{
    n=read(),m=read();
    for (int i=1;i<=n;i++){
        node[i]=read();
        pre[i]=i-1;
        nxt[i]=i+1;
        Q.push(make_pair(node[i],i));
    }
    pre[1]=n;
    nxt[n]=1;
    if (m*2>n){
        printf("Error!");
        return 0;
    }
    for(int i=1;i<=m;i++){
        greedy();
    }
    printf("%lld",ans);
    return 0;
}