[Usaco2013 Feb]Taxi

 

本人水平有限，题解不到为处，请多多谅解

 

本蒟蒻谢谢大家观看

 

题目：传送门

 

题目翻译如下：

贝西（Bessie）正在为农场的其他奶牛提供出租车服务。奶牛
沿着长度为M（1 <= M <= 1,000,000,000）的栅栏聚集在不同的位置。不幸的是，他们对
当前的位置感到厌烦，每个人都希望沿着篱笆走到其他地方。贝茜必须
在起跑点接她的每个朋友，然后开车送他们到目的地。贝茜的车很小，
所以一次只能运送一头母牛。奶牛可以立即进出汽车。
为了节省汽油，贝茜想尽量减少开车的次数。给定
N头奶牛中每头奶牛的开始和结束位置（1 <= N <= 100,000），请确定Bessie驾驶的最少驾驶量
去做。贝西意识到要节省最多的汽油，她可能偶尔需要将母牛放下到
目的地以外的其他地方。Bessie从栅栏的最左点开始，位置0，
并且必须在栅栏的最右点，位置M处完成旅程
。Bessie开出租车接人。整条路长度为M（1 <= M <= 10 ^ 9）。Bessie一开始在0号站，有N家客户（1 <= N <= 10 ^ 5）想要坐车，
它们会告诉Bessie这些在哪里以及它们的目的地。而Bessie的车太小了，一次只能坐一头牛。
为了省油，Bessie发现它每次不见得要把客户直接放在它的目的地，可以在中途放下之后再来接。
最后Bessie想问，它从0号站出发，接完所有的客户，最后到达M号站最少要走多少站？

输入项

*第1行：N和M以空格分隔。
*第2..1 + N行：第（i + 1）行包含两个以空格分隔的整数s_i和t_i（0 <= s_i，t_i <= M），
指示第i头母牛的起始位置和目的地位置。

输出量

第1行：一个整数，指示Bessie必须完成的驾驶总量。请注意，结果可能不适合32位整数。

样本输入

2 10
0 9
6 5
输入详细信息：有两头母牛等待沿着长度为10的围栏运输。
第一头母牛要从位置0（贝西开始的位置）移到位置9。
 第二头母牛希望从位置6转到位置5。

样本输出

12
输出详细信息：Bessie在位置0捡起第一头母牛，然后驱动到位置6。
她在那里放下第一头母牛，将第二头母牛运送到目的地，然后返回
捡起第一头牛。她放下第一头母牛，然后开车驶向其余的路
在栅栏的右边。
在0号站接第1个客户，从0号站出发到6号站（7站），放下第1个客户，接第2个客户，即可5号站再回来（2站），再接第1个客户，到达9号点（3站），共12站。（因为送完所有客户之后Bessie已在终点，故无需再走）


此题的贪心策略值得一思
首先我们可以肯定s_i 到 t_i 这段距离我们无论如何必须走到
接下来是考虑如何走回头路的问题
由图可知：回头路最小值应为不是同一对终点与起点的最小距离

 

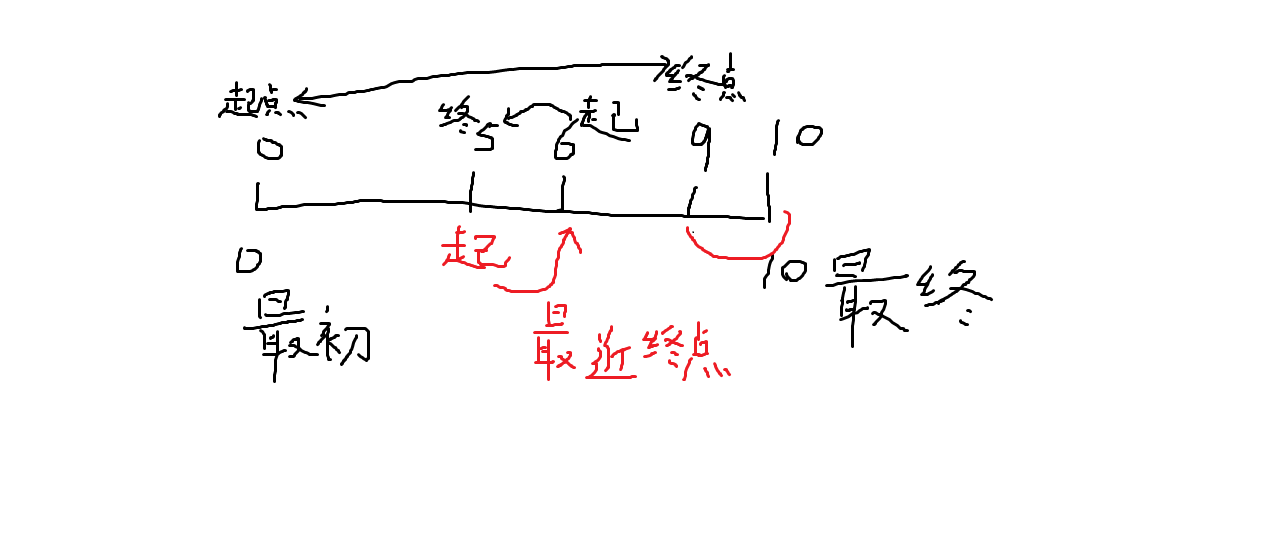
再看一幅图：

 

黑色为必经之路，红色为贪心策略之最短路，我们可以发现最初0与最末m也构成起点与终点，只不过样例中0已经为一头奶牛的起点，已经被算过了
反观回头路6，5在第一次中为第二头奶牛的初末点，在之后，我们以5为起点找到的最近的终点为6(或以6为终点找最近的起点)，将5→6作为回头路

注意：应当把0和m也放进起点与终点，在进行快排来确定最短距离

 code:

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
int s[100010],t[100010];
int ans=0;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();};
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*f;
}
signed main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++){
        s[i]=read(),t[i]=read();
        ans+=abs(s[i]-t[i]);
    }
    s[n+1]=m,t[n+1]=0;
    sort(s+1,s+n+2);
    sort(t+1,t+n+2);
    for(int i=1;i<=n+1;i++){
        ans+=abs(s[i]-t[i]);
    }
    printf("%lld\n",ans);
    return 0;
} 
/*
2 10
0 9
6 5
*/