树链剖分 [模板]最近公共祖先LCA
本人水平有限,题解不到为处,请多多谅解
本蒟蒻谢谢大家观看
题目:传送门
树链剖分:跑两遍dfs,第一遍找重边,第二遍找重链。
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径
son[]表示重儿子,top[]表示重链所在的第一个节点,sz[]表示子节点数,fa[]表示父亲节点
图示:
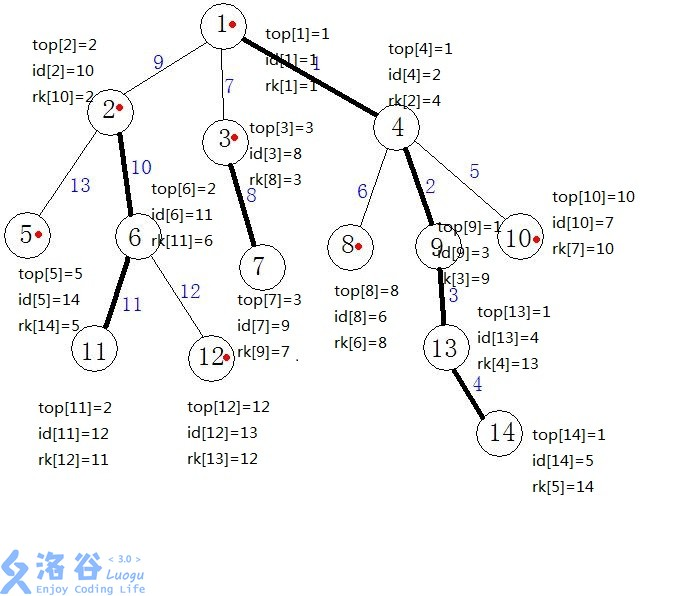
code:
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #pragma GCC optimize(3) 7 8 using namespace std; 9 int n,q,tot,s; 10 int head[1000010],nxt[10000010],ver[10000010],son[10000010],sz[10000010]; 11 int top[10000010],dep[10000010],fa[10000010]; 12 inline int read(){ 13 int x=0,f=1;char ch=getchar(); 14 while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} 15 while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} 16 return x*f; 17 } 18 inline void write(int x){ 19 char F[200]; 20 int tmp=x>0?x:-x ; 21 if(x<0)putchar('-') ; 22 int cnt=0 ; 23 while(tmp>0) 24 { 25 F[cnt++]=tmp%10+'0'; 26 tmp/=10; 27 } 28 while(cnt>0)putchar(F[--cnt]) ; 29 } 30 void add(int x,int y){//字符链 31 ++tot; 32 ver[tot]=y; 33 nxt[tot]=head[x]; 34 head[x]=tot; 35 } 36 void dfs1(int x){ 37 sz[x]=1;//自己算一个节点 38 son[x]=0;//自己的重儿子初始为0 39 for(int i=head[x];i;i=nxt[i]){ 40 int y=ver[i]; 41 if(y!=fa[x]){ 42 fa[y]=x;//上 : y 的父亲节点为 x 43 dep[y]=dep[x]+1;//中 : y的深度比x的深度多一 44 dfs1(y);//先遍历子树 45 sz[x]+=sz[y];// 下 :x的总结点数==字节点总数之和 46 if(sz[son[x]]<sz[y]) 47 son[x]=y; //不断更新重儿子 48 } 49 } 50 return ; 51 } 52 void dfs2(int x,int tp){//tp为x这条链的初始节点 53 top[x]=tp;//x的初始节点为tp 54 if(son[x]!=0)//若有重儿子 55 dfs2(son[x],tp);//遍历重儿子 56 //注意:此时重儿子的初始节点也为tp 57 for(int i=head[x];i;i=nxt[i]){ 58 int y=ver[i]; 59 if(y!=son[x]&&y!=fa[x])//如果y既不在重儿子中,也不可能为父亲节点 60 dfs2(y,y);//遍历y,因为son[x]已经遍历过了 61 } 62 } 63 int query(int u,int v){//查找u,v的LCA 64 while(top[u]!=top[v]){//如果u,v不在一条链上 65 if(dep[top[u]]<dep[top[v]])//如果u的深度浅的话,要交换 66 swap(u,v); //因为有可能向上跳的过程越过了LCA,保证深度必须超过其LCA 67 u=fa[top[u]];//向上跳 68 } 69 if(top[u]==top[v]){//如果在一条链上 70 if(dep[u]<dep[v])//输出深度浅的,因为深度越浅代表在上面,为u,v的LCA 71 return u; 72 else 73 return v; 74 } 75 } 76 int main() 77 { 78 n=read(),q=read(),s=read(); 79 for(int i=1;i<n;i++){ 80 int x,y; 81 x=read(),y=read(); 82 add(x,y),add(y,x); 83 } 84 dfs1(s);//以s为根 85 dfs2(s,s);//以s为根,s为初始节点 86 for(int i=1;i<=q;i++){ 87 int a,b; 88 a=read(),b=read(); 89 printf("%d\n",query(a,b)); 90 } 91 return 0; 92 }
树链剖分一定程度上类似于倍增,都是先确定大概范围,在具体寻找


