线性代数本质理解回顾(六)点积与对偶性
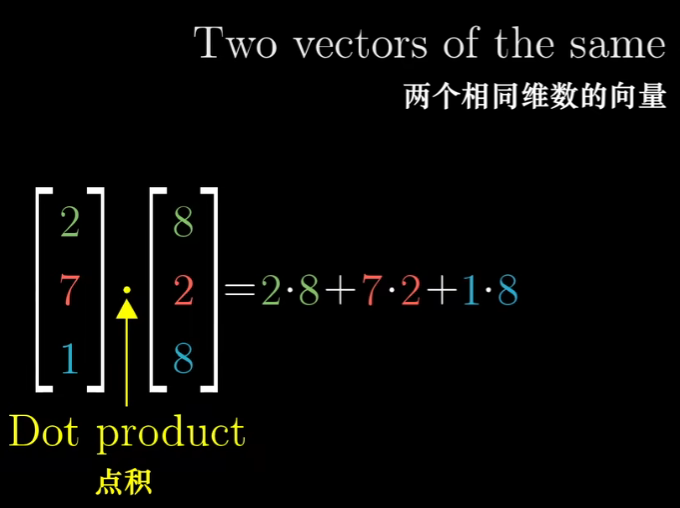
这个计算有一个完美的几何解释。


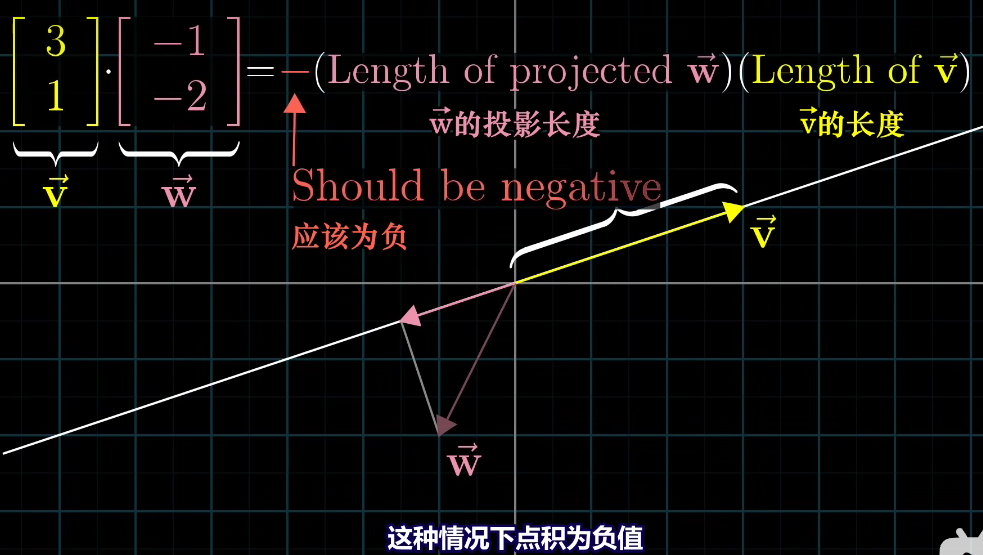
当两个向量的大致方向相同,则为正。若垂直 则为0. 若相反,则为负。
点积与顺序无关让我感到惊讶。直观上说说为什么无关,如果有对称性,则可以利用对称性。
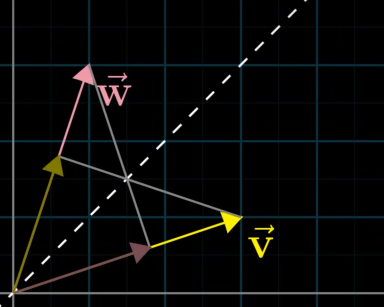
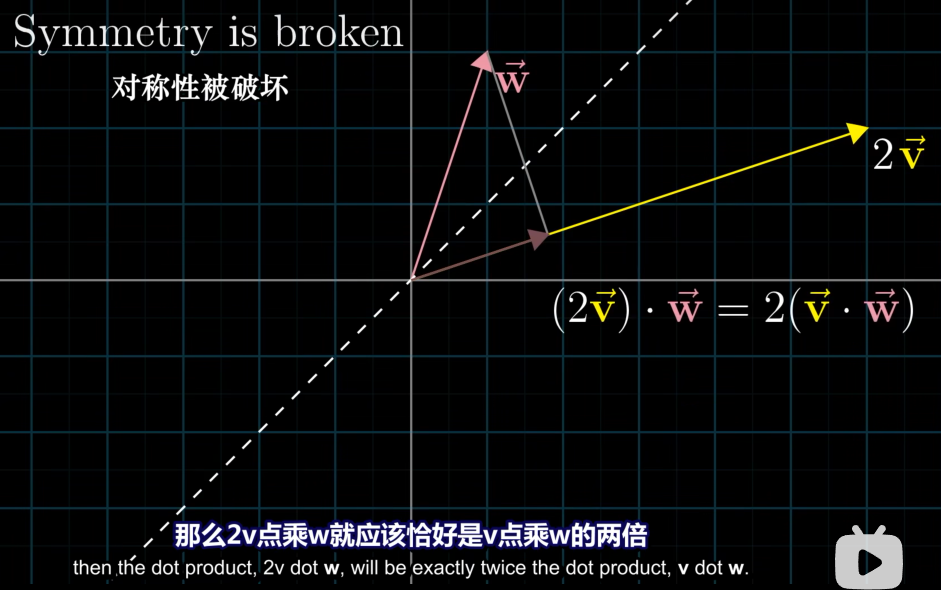
为什么点积是对应坐标相乘并将结果相加?


在继续深入之前,我想讨论一下 多维空间到一维空间的线性变换。

有不少函数能接收二维向量并输出一个数,
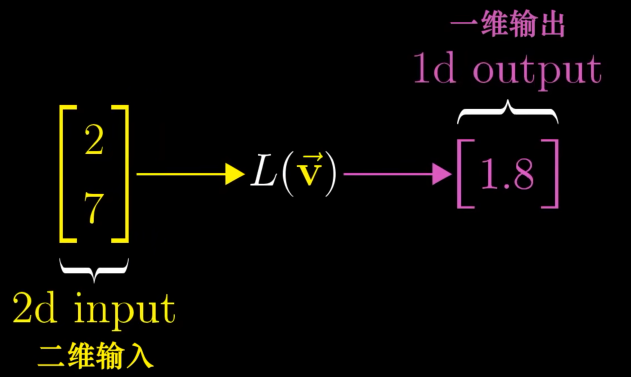
同样是二维输入和一维输出,和一般的函数相比,线性变换的要求更加严格。
如果你有一系列等距分布于一条直线上的点,然后应用变换 ,
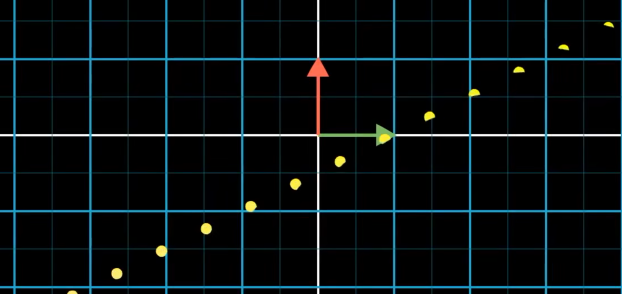
线性变换会保持这些点等距分布在输出空间中,也就是数轴上。

否则这些点没有等距分布,那么这个变换就不是线性的。
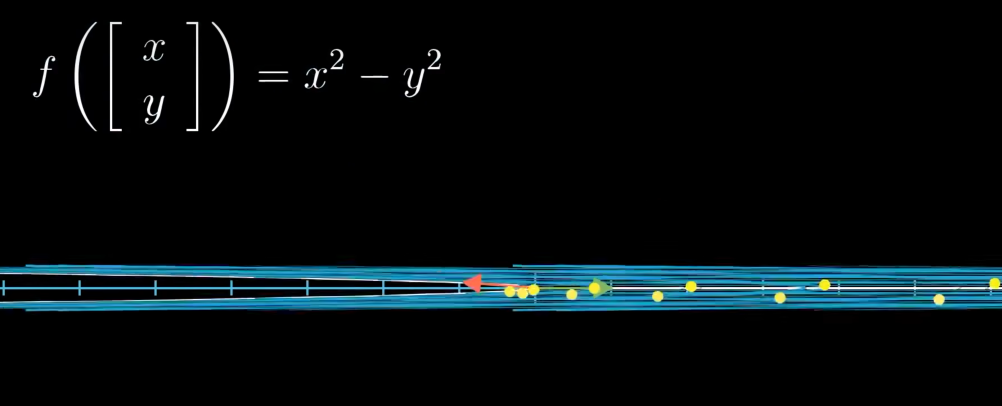
这些线性变换完全由它对i帽和j帽的变换决定。只不过,这些基向量这次只落在一个数上,

实际上,我们可以说1*2矩阵与二维向量之间有着微妙的联系,这种关系在于,将向量放到,从而得到与之相关的矩阵。

或者将矩阵立直,从而得到与之相关的向量。
将向量转化为数的线性变换和这个向量本身有着某种关系。
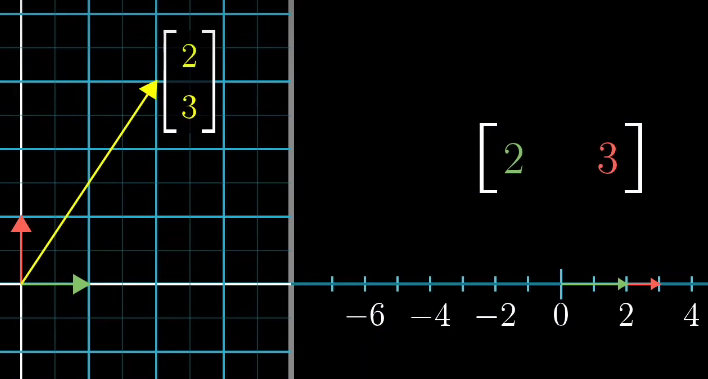
举个例子说明这种关系的重要性,而它恰恰回答了之间提到的点积的问题。
假设你还不知道点积与投影有关,我现在将数轴复制一份,然后保持0在原点,将它斜向放置在空间中,现在考虑这样一个二维向量,它的终点落在这条数轴的1上,我给它起个名字,就叫u帽,这个向量在接下来的讲解中扮演重要的角色。
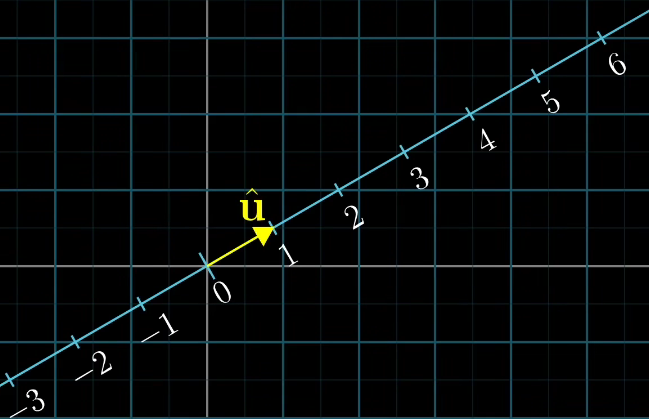
如果我们将二维向量直接 投影到这条数轴上,
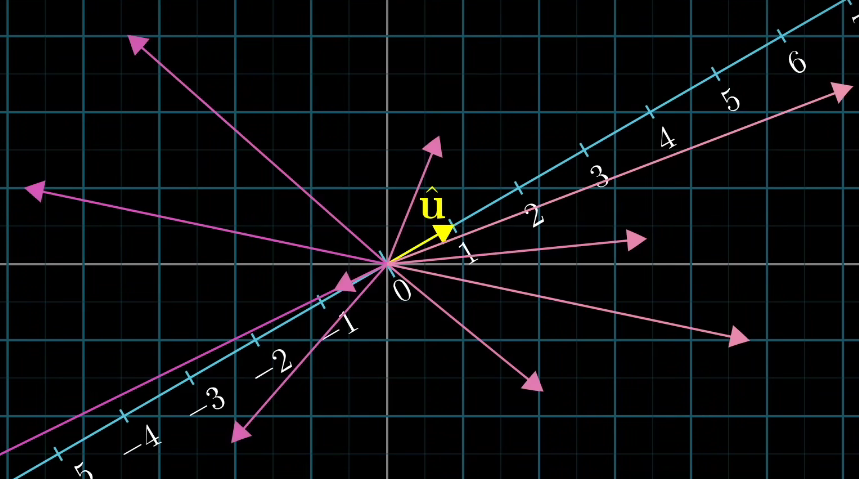
实际上,我们就这样定义了一个从二维向量到数的函数,
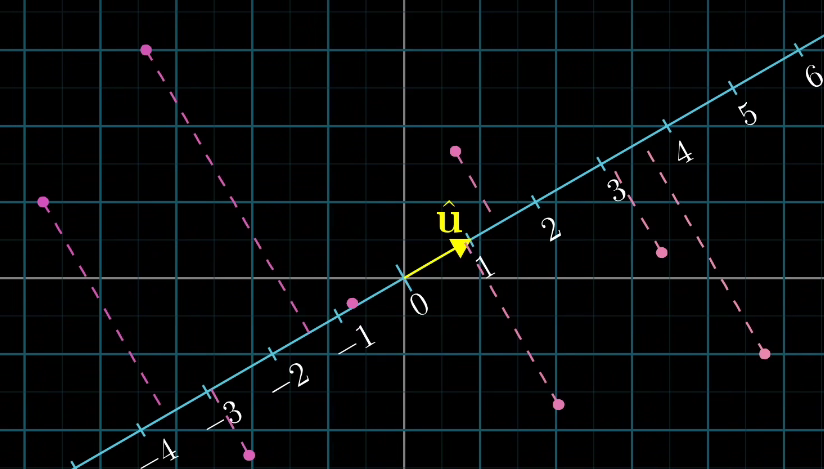
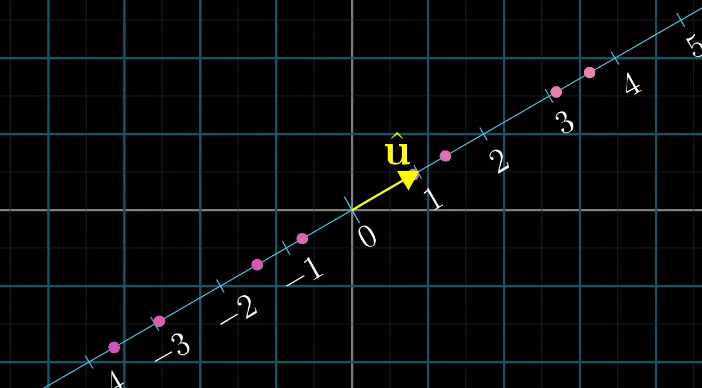
更重要的是,这个函数是线性的,因为它顺利通过了线性检验,即直线上等距分布的点在投影到数轴上后仍然等距分布。
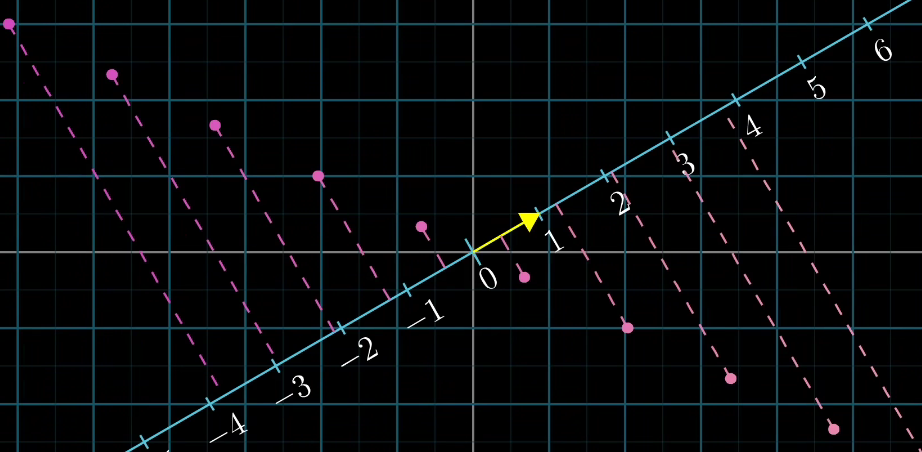
这里说明一点,即便我把这条数轴放在二维空间中,上述函数的输出结果还是数,而不是二维向量,你应该把它看作一个接受两个坐标并输出一个坐标的函数。
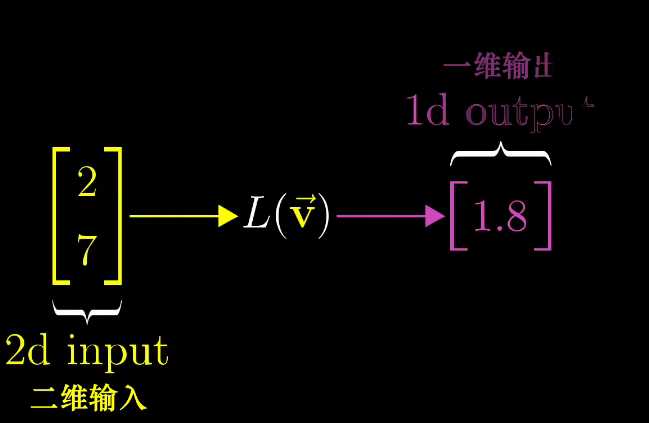
不过 u帽是二维空间中的一个向量, 而它又碰巧落在这条数轴上,根据这个投影,我们定义了一个从二维向量到数的线性变换,所以我们就能找到描述这个变换的1*2矩阵。
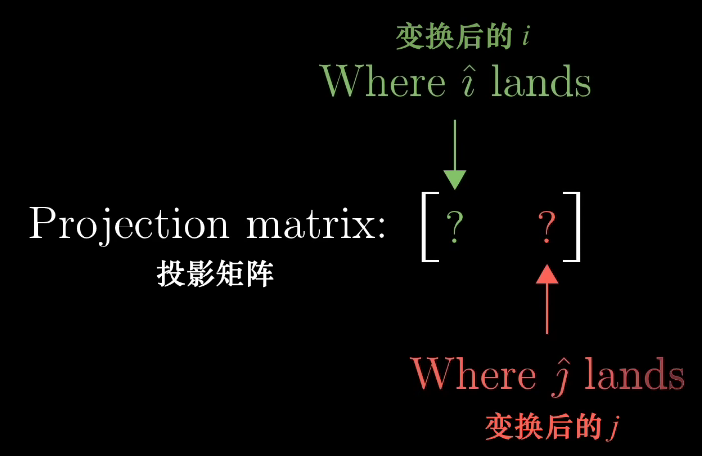
为了找到这个矩阵,我们把这条数轴放大来看,并且需要考虑变换后i帽和j帽的位置,因为它们就是矩阵的列,这一部分内容超级漂亮。我们可以通过精妙的对称性进行推理,因为i帽和u帽都是单位向量,

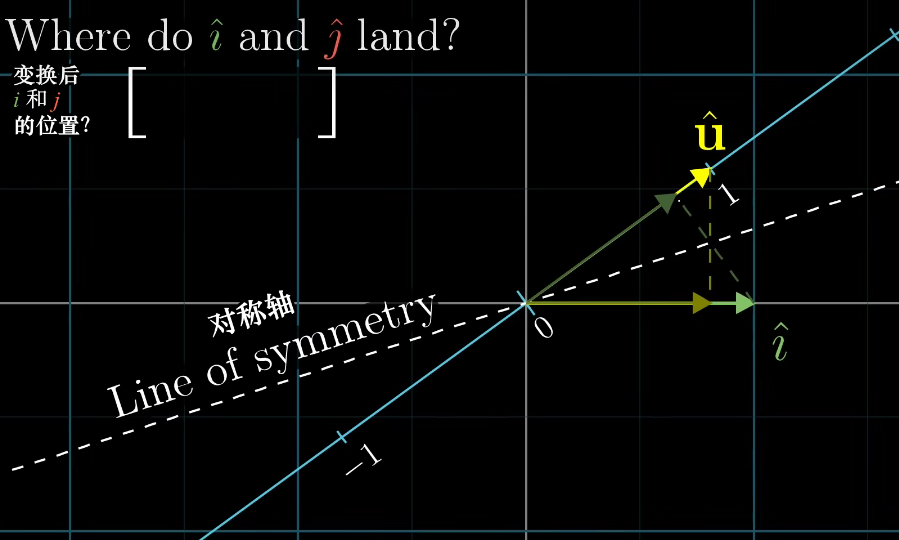
所以说,如果要问i帽在投影之后落在哪个数上,答案就是u帽向x轴投影所得到的数, 而u帽向x轴投影得到的数就是u帽的横坐标。因此根据对称性,将i帽向斜着的数轴上投影所得到的数,就是u帽的横坐标,
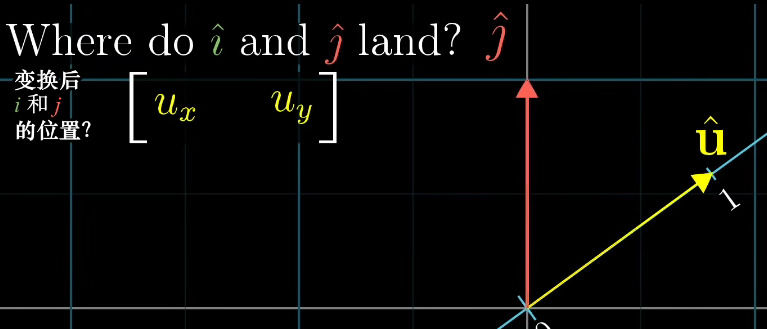



 浙公网安备 33010602011771号
浙公网安备 33010602011771号